Subtracting Larger Numbers
MULTIDIGIT SUBTRACTION METHODS

Develop Multiple Methods
In this unit, students develop meaningful, accurate, and efficient methods for subtraction of … read more
Develop Multiple Methods
In this unit, students develop meaningful, accurate, and efficient methods for subtraction of two-digit numbers. The unit includes opportunities for students to practice both addition and subtraction in various contexts so that they learn to choose computation methods based on the context and the numbers in the problem.
The development of computation methods in Math Trailblazers is based on research that corroborates the relationship between conceptual understanding and procedural fluency (Fuson & Burghardt, 2003; Fuson, 2003; Verschaffel et al., 2007; National Research Council, 2001; NCTM, 2000; Hiebert & Wearne, 1996). In this unit, students develop their own methods for subtraction to first solve word problems and then to solve problems with two-digit numbers using base-ten pieces. With these opportunities, students make connections between their understanding of place value and procedures for subtraction. As stated in Adding It Up: Helping Children Learn Mathematics, “Opportunities to construct their own procedures provide students with opportunities to make connections between the strands of proficiency¹. Procedural fluency is built directly on their understanding. The invention itself is a kind of problem solving, and they must use reasoning to justify their invented procedure. Students who have invented their own correct procedures also approach mathematics with confidence rather than fear and hesitation” (Kamii and Dominick, 1998) (National Research Council, 2001, p. 197).
Throughout the unit, students share their own strategies with their classmates. See Figure 1. Comparing the various strategies and trying them out allows students to analyze the efficiency and usefulness of the methods in different situations (NCTM, 2000, p. 153).
Subtraction Strategies Menu
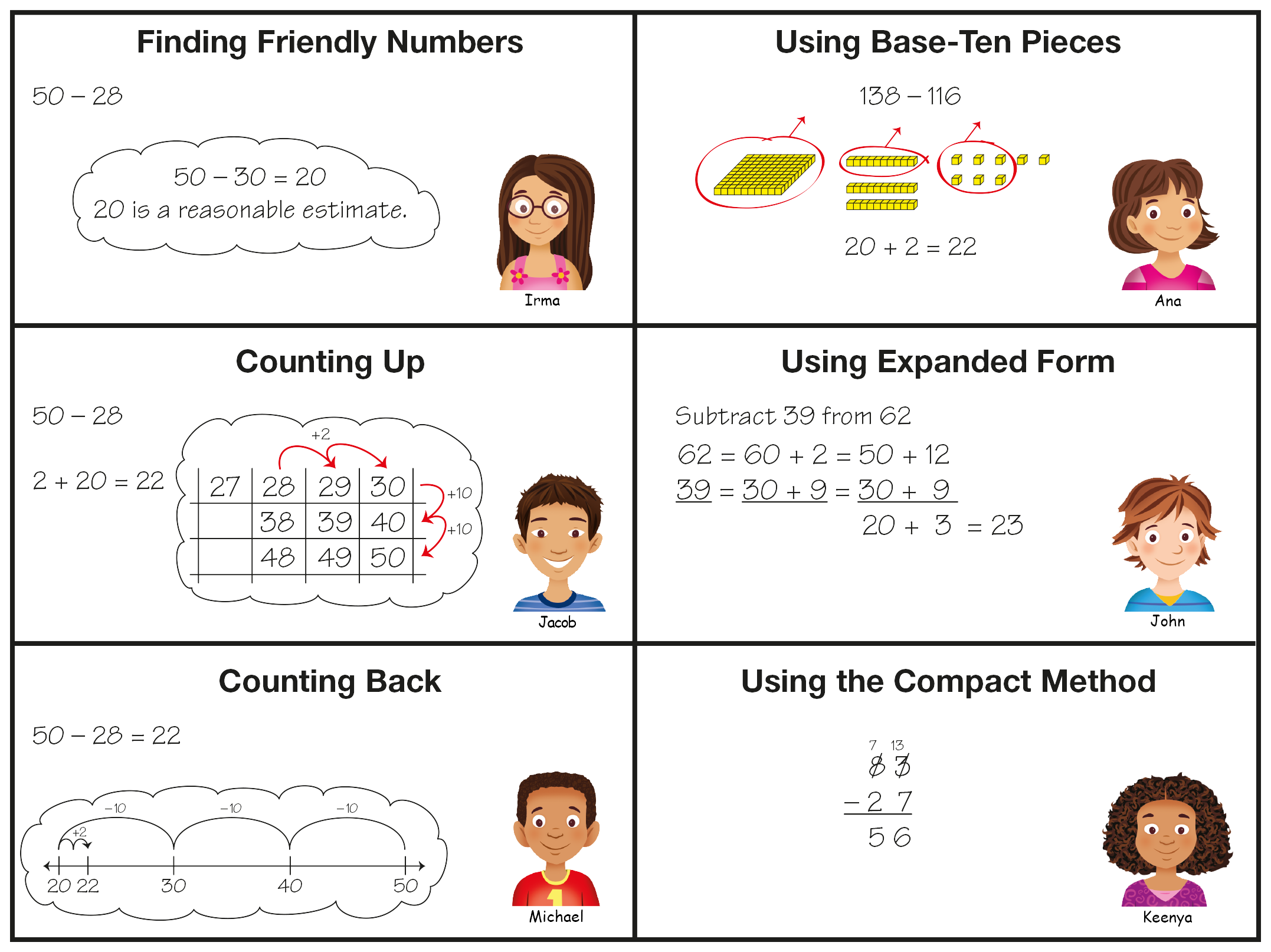
Figure 1: A menu of subtraction strategies discussed in this unit
¹The strands of mathematical proficiency include conceptual understanding, procedural fluency, and productive disposition. (National Research Council, 2001, p. 5)
Develop Paper-and-Pencil Methods for Subtraction
In this unit, students learn the algorithm that is traditionally taught in the … read more
Develop Paper-and-Pencil Methods for Subtraction
In this unit, students learn the algorithm that is traditionally taught in the United States. To use the algorithm efficiently and accurately, students need a solid understanding of place value in the base-ten system. Therefore, students build on their previous experiences with base-ten pieces to develop meaning for the algorithm. Base-ten pieces are effective if students are given enough time to think for themselves how to compose and decompose numbers in order to take away a quantity. Then, students need to connect the process with the base-ten pieces to written symbols (National Research Council, 2001, p. 198; Fuson and Burghardt, 2002, pp. 289–290).
Subtraction Computation
The standard algorithm for subtraction poses unique challenges to young … read more
Subtraction Computation
The standard algorithm for subtraction poses unique challenges to young learners. Subtraction computation is more difficult than addition because subtraction involves a more complex regrouping process.
We offer several recommendations to facilitate acquisition of subtraction skills.
- Allow students to use addition and subtraction methods that make sense to them.
- Encourage students to use a variety of problem-solving methods that are appropriate to the situation and to their understanding.
- Have students compare various problem-solving methods using criteria such as speed, ease of use, and accuracy.
- Help students make connections between various addition and subtraction problem-solving methods.
One of the goals of this unit is to expand students’ view of computation possibilities. It is important for students to recognize that the traditional paper-and-pencil algorithm is just one among many acceptable methods of finding the answers to subtraction and addition problems.
From our research, we have found that students sometimes make the errors shown in Figure 2. Similar errors were found in other research studies (Fuson and Burghardt, 2003, p. 286). In A, the student subtracted the smaller number from the larger in each column, possibly thinking only of the individual digits instead of the value of each place. In B and C, the students did not trade correctly. Students who make these mistakes often do not understand that when they make trades the value of the top number, the minuend, should not change. Students should be able to look back at their trades and decide if the new partition represents the same number. For example, writing a number sentence for the trades recorded for B (70 + 15 = 85), shows that the new groupings equal 85 instead of 75. Asking students to think about the value of the digits and to link their written method with base-ten pieces will often help students correct their own errors (Fuson and Burghardt, 2003, p. 289).

Figure 2: Possible subtraction errors
Students often make the mistake in Error C when they have a zero in the minuend. When students have multiple strategies to choose from, they can solve similar problems using other efficient strategies that may result in greater accuracy. For example, students can first subtract 50 from 90 and then add 3 (90 − 50 = 40; 40 + 3 = 43), or they can count up from 47 (47 + 3 = 50, 50 + 40 = 90, so the answer is 3 + 40 = 43.) See the strategy Counting Up in Figure 1.
Checking for Reasonableness and Accuracy
This unit includes activities that encourage students to either estimate to see if their answer is … read more
Checking for Reasonableness and Accuracy
This unit includes activities that encourage students to either estimate to see if their answer is reasonable or to check their work for accuracy. Students can check for accuracy in subtraction by solving the problem using a mental strategy or adding the answer to the number subtracted and checking to see that the sum equals the number they started with.
MATH FACTS and MENTAL MATH

Subtraction Facts
The goal of the math facts development in Math Trailblazers is for students to learn the basic math facts efficiently, gain fluency with … read more
Subtraction Facts
The goal of the math facts development in Math Trailblazers is for students to learn the basic math facts efficiently, gain fluency with their use, and retain that fluency over time. A large body of research supports an approach in which students develop strategies for figuring out the facts rather than relying on rote memorization. This not only leads to more effective learning and better retention but also to the development of mental math skills. In fact, too much drill before conceptual understanding may interfere with a child’s ability to understand concepts at a later date.
The research that contributed to the National Council of Teachers of Mathematics Principles and Standards for School Mathematics and the National Research Council’s Adding It Up has informed the structure of the math facts strand in Math Trailblazers. Also see the Letter Home for more about the development of the basic facts in Math Trailblazers in Second Grade.
In Grade 2 Unit 1, students began the yearlong, strategies-based program for developing and maintaining fluency with the addition and subtraction facts. Items in the Daily Practice and Problems (DPP) in Units 1–8 focused on the addition facts. In Unit 9 students begin the systematic study of the subtraction facts. The subtraction facts are studied in the same groups as were the addition facts, one group per unit. See the chart in Figure 3 for the distribution of the practice and assessment of the subtraction facts in Units 9–15.
Daily Practice and Problems items in this unit can be used to assess students’ abilities to solve the subtraction facts related to the addition facts in Group A.
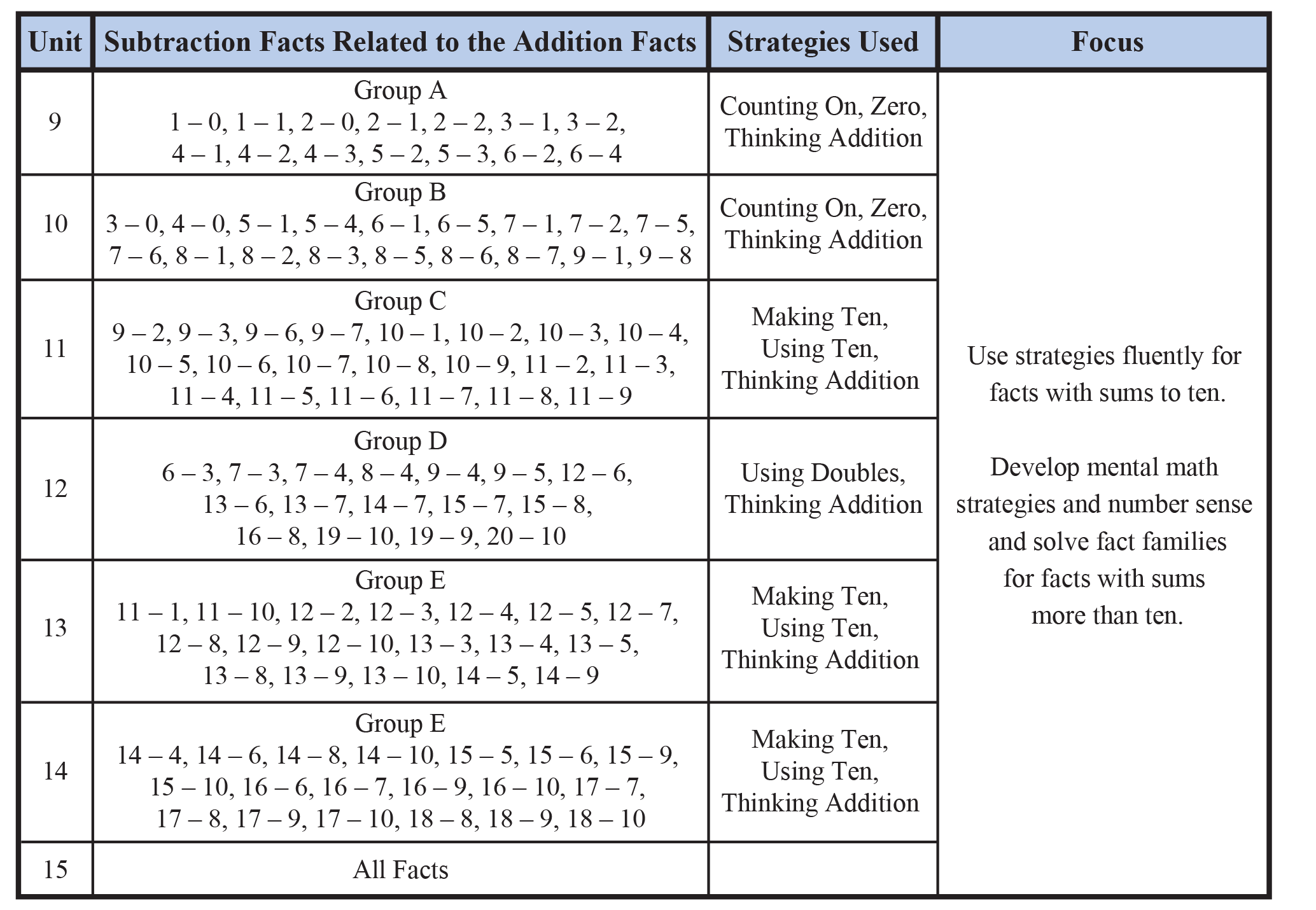
Figure 3: Development of related subtraction facts in Grade 2
Strategies-Based Approach
Students first work on groups of facts that lend themselves to simple strategies before moving on to work with groups of … read more
Strategies-Based Approach
Students first work on groups of facts that lend themselves to simple strategies before moving on to work with groups of facts that require more sophisticated strategies. Common strategies for subtraction facts include the following:
- Using counters. This is a particularly straightforward strategy. It is effective, especially for small numbers, and is usually well understood by students. However, it is not a very efficient method for larger numbers.
- Counting up. This is a natural strategy, particularly for subtracting 1, 2, or 3. A student starts with the smaller number and counts up to the larger number, keeping track of how many numbers he or she counts up, perhaps using fingers.
- Counting back. This is a strategy very similar to counting up. It works best for subtracting 1, 2, or 3. The student starts with the larger number and counts back to the other number.
- Using doubles. The addition doubles, e.g., 4 + 4 = 8 and 6 + 6 = 12, can be used to learn the subtraction
“half-doubles” as well:
8 − 4 = 4 and 12 − 6 = 6. These facts can then be used to figure out close facts, such as 9 − 4 = 5 and 13 − 6 = 7. - Making 10. Knowing the addition facts that have a sum of 10, e.g., 8 + 2 = 10, is helpful in finding
differences from 10,
e.g., 10 − 8 = 2 and 10 − 2 = 8. Students can use ten frames to visualize these problems as shown in Figure 4. - Using 10. Students follow the pattern they find when subtracting 10, e.g., 13 − 10 = 3 and
15 − 10 = 5, to learn close facts,
e.g., 13 − 9 = 4 and 15 − 9 = 6. Since 13 − 9 will be 1 more than 13 − 10, they can reason that the answer will be 4, or 3 + 1. - Reasoning from related addition and subtraction facts (fact families). Students study fact families to reinforce their understanding that addition and subtraction are related. Knowing 4 + 2 = 6 helps students solve 6 – 4. Reasoning from known facts is a powerful strategy for those who can apply it and should be encouraged.

Figure 4: A ten frame showing 10 − 2 = 8 and 10 − 8 = 2
References
- Fuson, K.C. “Developing Mathematical Power in Whole Number Operations.” In A Research Companion to Principles and Standards for School Mathematics. J. Kilpatrick, W.G. Martin, and D Schifter, eds. National Council of Teachers of Mathematics, Reston, VA, 2003.
- Fuson, K.C. and B.H. Burghardt. “Multidigit Addition and Subtraction Methods Invented in Small Groups and Teacher Support of Problem Solving and Reflection.” In The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise. A.J. Baroody, A. and A. Dowker, eds. Lawrence Erlbaum Associates, Mahwah, NJ, 2003.
- Hiebert, J., and D. Wearne. “Instruction, Understanding, and Skill in Multidigit Addition and Subtraction.” Cognition and Instruction, 14(3), pp. 251–283, 1996.
- National Research Council. “Developing Proficiency With Whole Numbers.” In Adding It Up: Helping
Children Learn Mathematics.
J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001. - Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- Verschaffel, L., B. Greer, and E. Decorte. “Whole Number Concepts and Operations.” In Second Handbook of Research on Mathematics Teaching and Learning. F.K. Lester, Jr., ed. Information Age Publishing Inc., Charlotte, NC, 2007.












