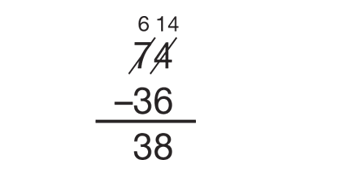Subtraction with No Trades.
Introduce the lesson by
having students solve a problem with no trades such as
46 – 14. Ask students to solve the problem using
base-ten pieces and the expanded form notation. Have
a student volunteer demonstrate the solution to the
problem.
Next explain that you will show another way to record
the solution with paper and pencil. Use the display of
the Base-Ten Recording Sheet Master to demonstrate
the same subtraction problem using base-ten pieces
and the paper-and-pencil compact method. Have students
represent the problem simultaneously on the Base-Ten Recording Sheet page in the Student Activity Book.
- What pieces did [student name] use to show the
number 46? (4 skinnies and 6 bits)
- Place the base-ten pieces on your desk to show the
number 46.
- Then write the number of skinnies in the tens column
and the number of bits in the ones column on
the Base-Ten Recording Sheet.
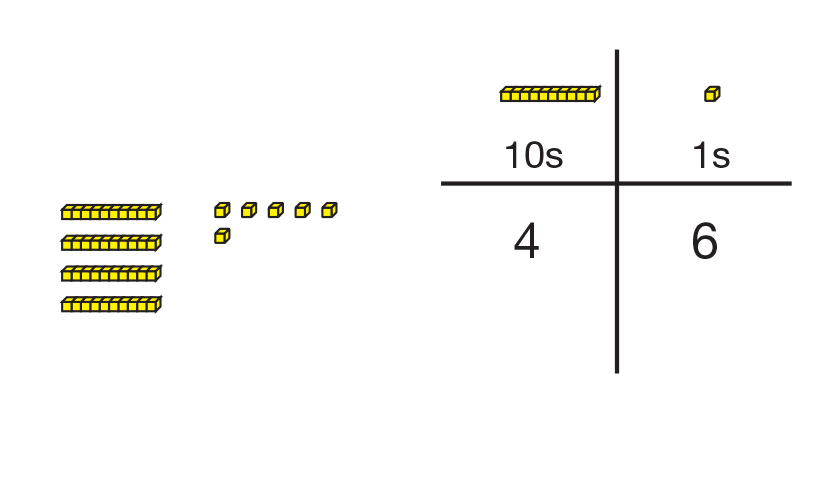
Demonstrate by placing 4 skinnies and 6 bits on the
display of the Base-Ten Recording Sheet. Then write 4
in the tens column and 6 in the ones column as in Figure 1.
On the next line of the table, write “ – 14” to indicate
that you will take 14 away from 46 and have students
do the same on their recording sheet. Draw a line
underneath.
- How many bits does this say you should take
away? (4 bits)
Demonstrate by taking 4 bits away and have students
do the same with their base-ten pieces.
- How many bits do you have left? (2 bits)
- Write 2 in the ones column under the 4 to show that.
- What do you need to take away next? (one skinny or one ten)
Demonstrate by taking 1 skinny away and have students
do the same.
- How many skinnies do you have left? (3 skinnies)
- Where should you write the answer? (in the tens column—under the one)
Record the solution for the problem as shown in Figure 2.
- How many base-ten pieces are left for the
answer? (three skinnies and 2 bits or 32)
- What do the 3 skinnies represent? (3 tens or 30)
- What do the 2 bits represent? (2 ones or 2)
Subtraction with Trades. Next solve a problem that
involves trading such as 46 − 27. Use the display of
the Base-Ten Recording Sheet Master to demonstrate
the problem as you guide students to demonstrate the
problem on the recording sheet in the Student Activity
Book. See Figure 3. Write 46 − 27 on the display.
- What base-ten pieces do you use to represent
46? (4 skinnies and 6 bits)
Place the base-ten pieces on the recording sheet as students
do the same on their recording sheets.
Point to the 7 in the number 27. Ask:
- How many ones does this say you should take away? (7 ones)
- Is it possible to take 7 bits away from 6 bits? (No, there aren’t enough.)
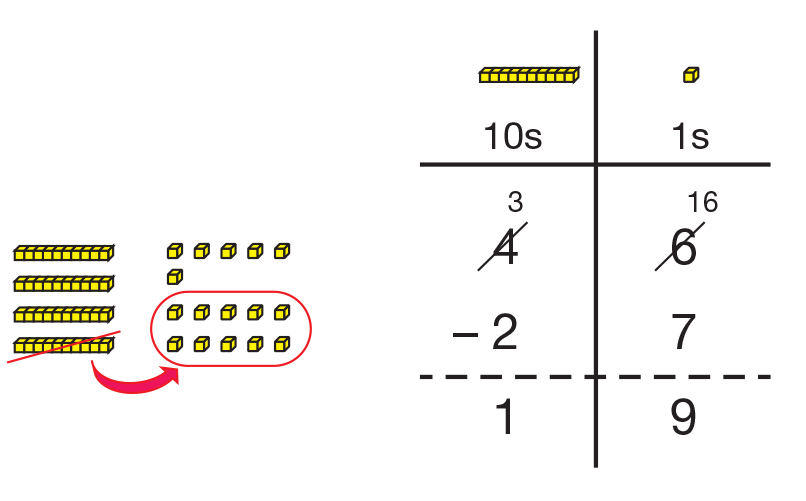
- What should you do? (Possible response: You can trade 1 skinny for 10 bits.)
Remove a skinny and replace it with
10 bits. Ask:
- Add the 10 bits to the 6 that were there. How many
bits do you have now? (16 bits)
- To show that you have 16 bits now, cross out the 6
in the ones column and change it to 16.
- How many skinnies do you have now? (3 skinnies)
- Since you took 1 skinny from the 4 skinnies, cross
out the 4 in the tens column and write 3.
- Is 3 skinnies and 16 bits the same as 4 skinnies and 6 bits? (Yes. We traded one skinny for 10 bits but all the pieces still add to 46.)
- Do you have enough bits now to take away 7 bits? (yes)
Take 7 bits from the 16. Ask:
- What is 16 – 7? (9)
- Now subtract 3 skinnies – 2 skinnies.
Demonstrate taking away 2 skinnies from the 3 skinnies and have students do the same. Ask:
- How many tens or skinnies do you have
left? (1 skinny)
- What is the answer? (Possible response: I have
1 skinny and 9 bits. That’s 19.)
Have students model a problem such as 253 – 117.
- What base-ten pieces do you use to represent 253? (2 flats, 5 skinnies, and 6 bits)
Place the base-ten pieces on the recording sheet as students do the same on their recording sheets.
Point to the 7 in the number 117. Ask:
- How many ones does this say you should take away? (7 ones)
- Is it possible to take 7 bits away from 3 bits? (No, there aren’t enough.)
- What should you do? (Possible response: You can trade 1 skinny for 10 bits.)
Remove a skinny and replace it with
10 bits. Ask:
- Add the 10 bits to the 3 that were there. How many
bits do you have now? (13 bits)
- To show that you have 13 bits now, cross out the 3
in the ones column and change it to 13.
- How many skinnies do you have now? (4 skinnies)
- Since you took 1 skinny from the 5 skinnies, cross
out the 5 in the tens column and write 4.
- Is 2 flats, 5 skinnies, and 3 bits the same as 2 flats, 4 skinnies, and 13 bits? (Yes. We traded one skinny for 10 bits but all the pieces still add to 253.)
Count out the base-ten pieces with
students. Ask:
- Do you have enough bits now to take away 7 bits? (Yes.)
Take 7 bits from the 13. Ask:
- What is 13 − 7? (6)
- Now subtract 4 skinnies − 1 skinny.
Demonstrate taking away 1 skinny from the 4 skinnies and have students do the same. Ask:
- How many tens or skinnies do you have
left? (3 skinnies)
- Subtract 2 flats − 1 flat. What is the answer? (1 flat)
- What is the answer? (136)
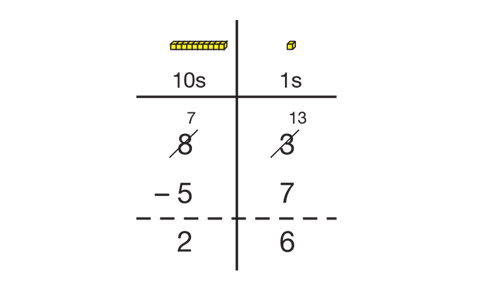
Ask students to solve a problem such as 83 – 57 that
requires trades, but do not ask them to use base-ten
pieces to model
it—instead ask them to imagine they
have base-ten pieces. See Figure 4. Begin by writing
the problem on the display of the Base-Ten Recording Sheet.
- If you used base-ten pieces to solve this problem, how many skinnies and bits would you start with
and how many do you need to take away? (Possible response: You would start with 8 skinnies and 3 bits and you need to take away 5 skinnies and 7 bits.)
- Is it possible to take 7 bits away from 3 bits? (No,
you have to trade.)
- Imagine the trade in your head. What will
you do?
Give students time to decide how to make
the trade.
- What did you think in your heads? What did you trade? (1 skinny for 10 bits)
- If you trade one of the skinnies for 10 bits, how many bits do you have? (You have 10 bits plus 3 bits. That’s 13 bits.)
- Let’s write that down. I’ll cross out the 3 bits and write 13 in the ones column. That shows the 13 bits.
- Do you still have 8 skinnies? (No. We took away
one skinny when we traded. So now we only have 7 skinnies.)
- How do you show that? (Possible response: Cross
out the 8 in the tens column and write a 7 for 7 tens.)
- Is 7 tens and 13 ones the same as 8 tens and
3 ones? (Yes. You changed the number of bits and
skinnies but they add up to the same number. 8 tens
and 3 ones is the same as 7 tens and 13 ones. They
are both 83.)
- Finish the problem. Look at the ones column. What is 13 – 7? (6)
- Look at the tens column. What is 7 – 5? (2)
- What is the answer? (26)
Pose a few more problems that involve trades with
three-digit numbers involving only one trade such as
243 – 128 and explain how it is similar to subtracting
a two-digit minus a two-digit number but with hundreds.
Have students solve them on their Base-Ten Recording Sheet. As you discuss the problems, ask students
to imagine base-ten pieces.
If students have difficulty understanding how to solve a
three-digit minus a three-digit problem, cover the hundreds
column and point out that students could solve the problem
as a two-digit minus a two-digit problem and then subtract
the hundreds. If the trade is in the hundreds column, cover
the hundreds and tens columns and have students subtract
in the ones column and then go on to making trades from the
hundreds column to the tens column.
After the class has solved several problems, ask students
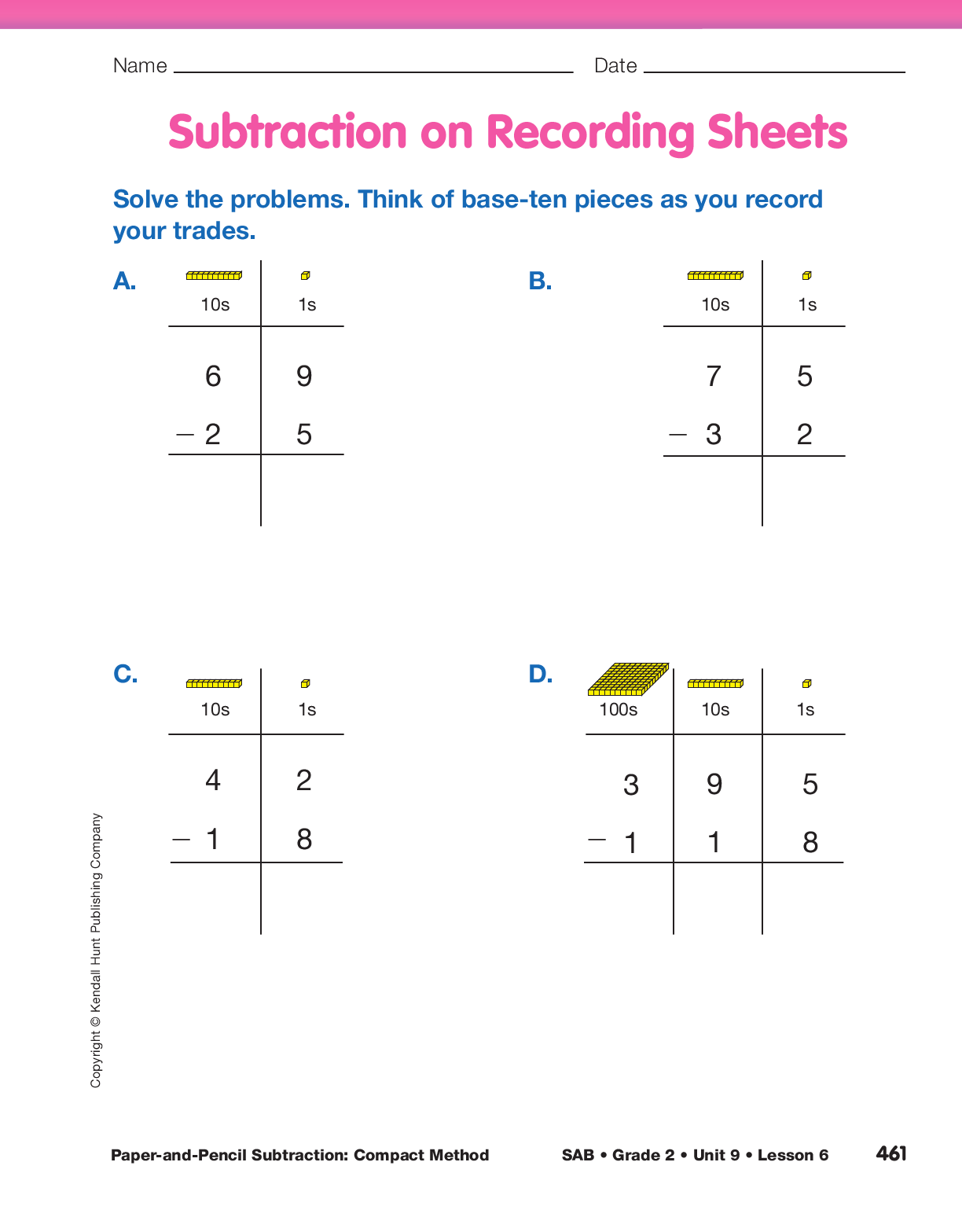
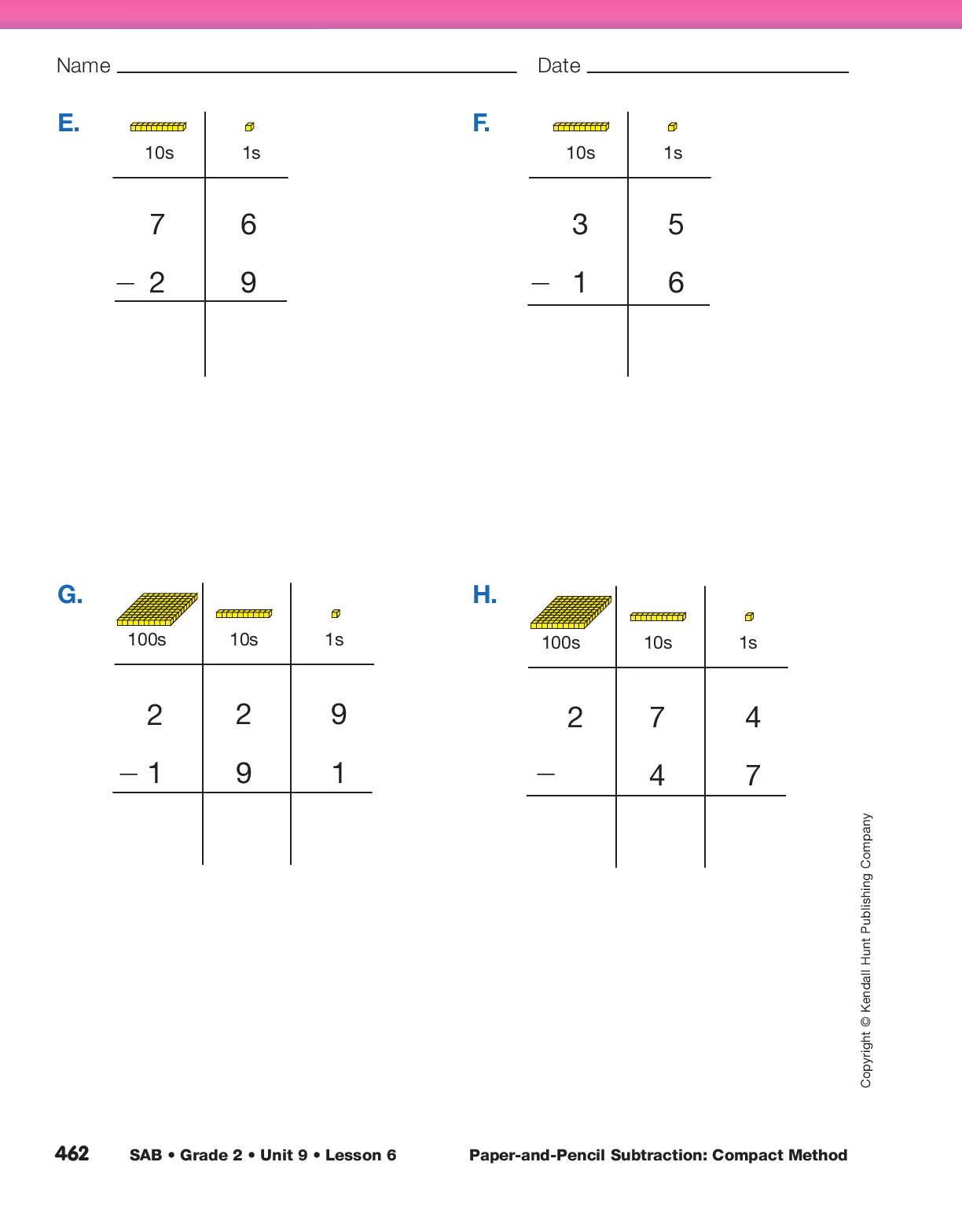
to solve the problems on the Subtraction on Recording Sheets pages in the Student Activity Book.
As students work on the problems at their desks, ask
individual students to explain the procedure for
solving the problem and to relate their thinking to base-ten pieces.
If students have difficulty imagining the base-ten pieces as
they solve the problems using the compact method, have
base-ten pieces available until they develop an understanding
of how the compact method relates to the base-ten pieces.
Recording Trades with the Compact Method. Have students solve more subtraction problems, but
do not use the recording sheets. Write a problem on a display such as 74 − 36. Guide students as they solve the problem.
- For this problem, there are no labels for the
columns and lines to separate the tens and ones.
Which column is the ones column and which is the
tens column? (Possible response: The ones column
is on the right and the tens column is next to
the ones column to the left.)
Solve the problem together using the same procedure
as before but without the recording sheet or
base-ten pieces as shown in Figure 5.
Ask questions
that connect the numbers written and crossed out
with base-ten pieces and place value:
- Let’s start with the ones column. Which column is that? (the column on the right)
- Is it possible to take 6 away from 4? (no)
- If you solved it with base-ten pieces, what would you do? (Trade a skinny for 10 bits.)
- If you trade a skinny for 10 bits, how many skinnies and bits will you have? (6 skinnies and 14 bits)
- How can you record that? (Cross out the 7 in the tens column and make it 6. Then cross out the 4 in the ones column and make it 14.)
- Now finish the problem by subtracting 14 – 6 in the ones column and 6 – 3 in the tens column.
- Is 38 a reasonable answer? (Possible response: Yes. I used friendly numbers. 74 – 36 is about the same
as 75 – 35 or 40 and 40 is close to 38.)
Have students complete the Compact Subtraction
page in the Student Activity Book. Upon completion,
ask student volunteers to explain their solutions to
the class. Encourage the class to ask questions about
the way the problems are recorded and to check the
answers to make sure they are reasonable.