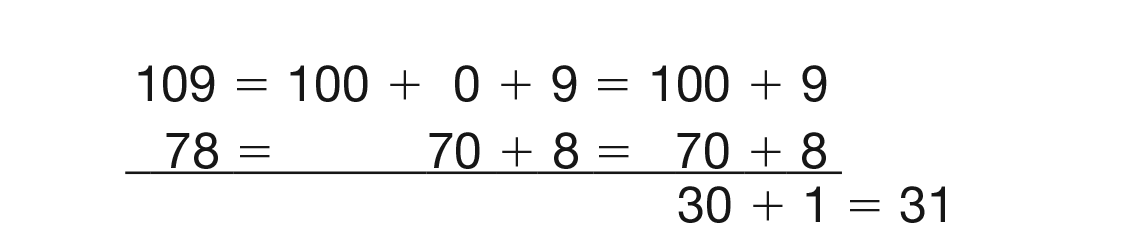Display the problem 109 − 78 and ask a student to
explain how he or she estimates the difference. Then
ask a student to show how to solve 109 − 78 using
the expanded form paper-and-pencil method. See
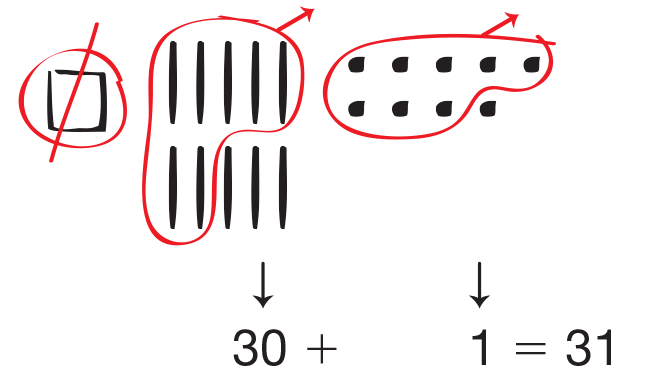
Figure 8. Have another student use display base-ten
pieces and the Fewest Pieces Rule to set up the problem,
and then show the trades. See Figure 9.
Ask questions similar to the following to discuss how the two solutions are connected:
- What base-ten pieces did [student name] use to represent 109? (1 flat and 9 bits)
- Why aren’t there any skinnies? (There are no tens
in 109.)
- Can you take 7 tens away from 0 tens? (no)
- When [student name] subtracted 78, were any
trades made? Why? (Yes, one trade was made
because you can’t take 7 skinnies away from
0 skinnies.)
- Explain the trade. (1 flat was traded for 10 skinnies.)
- How many skinnies did [student name] have to
work with after the trade? (Since there weren’t
any tens to begin with in 109, 0 skinnies plus
10 skinnies is just
10 skinnies.)
- Besides using a flat, can anyone think of another
way to represent 100 with base-ten pieces? (Possible response: Yes, you could put 10 skinnies
down for 100 right away. Then you could just start subtracting.)
- Is 10 skinnies and 9 bits the same as 1 flat and
9 bits? (yes)
- When [student name] wrote the problem, how did
[he] show that 109 doesn’t have any tens? How
were the numbers lined up? (He lined up the
numbers so the hundreds were aligned with the
hundreds, the tens with the tens, and the ones
with the ones. Since 109 doesn’t have any tens,
there is a 0 in the tens column.)
- How were the trades shown on [student name]’s
paper-and-pencil solution? (The 0 in the tens column was regrouped as 100.)
- When you use expanded form, how can you tell if
you partitioned a number correctly? For example,
in this problem, is 100 + 0 + 9 the same as
100 + 9? (Yes, both equations have to equal the
number you started with, 109.)
- Does 100 + 9 = 100 + 10 + 9? Which is a correct
partitioning of 109? (no; 100 + 9 is correct, but
100 + 10 + 9 is wrong.)
- Show how to check this problem with addition.
(Add the answer 31 to 78, which is 109, the number we started with, so 31 is correct.)
To conclude the lesson, ask:
- Think about other subtraction strategies you have
used. Do you like the expanded form
paper-and-pencil method? Why or why not?
- Think about solving problems with base-ten
pieces and with expanded form. Do both ways
help you find correct answers?
- Which do you find more efficient: using the
base-ten pieces or the expanded-form method?
Why?
- Is one way easier for you than the other? Why?
Assign the Expanded Form Subtraction Assessment
Master for students to complete individually.
Provide access to base-ten pieces for students who
choose to use them.
Use the Expanded Form Subtraction Assessment Masters
with the Feedback Box to assess students’ abilities to use and
apply place value concepts [E1]; represent subtraction
problems using base-ten pieces [E2]; subtract multidigit
numbers using base-ten pieces [E3]; subtract multidigit
numbers using expanded form [E4]; estimate differences
using mental math strategies [E5]; check for reasonableness
[MPE3]; and use addition to check subtraction
calculations
[MPE4].
Assign the Solve and Check Homework Masters
after Part 2 of this lesson.