Dimes, Nickels, and Quarters

Count On to Find the Value of Coins. Using a display set of coins, show 4 nickels and ask the students to identify the total value. Ask for different strategies for finding the value, but make sure that skip counting by fives is discussed. Then give the students a few minutes to find different ways they can make 20 cents, such as 2 dimes, 1 dime and 2 nickels, etc., and record them on the display.

Then display a quarter and 3 dimes.

Students may suggest skip counting by tens to start. If so, let them model this.

If no one suggests it, direct students to the 100 Chart. Ask if anyone remembers skip counting by tens when starting at a point other than zero (Units 9 and 10).

Point to each number on the chart while the students count with you: 25, 35, 45, 55.

Display a few more combinations of coins for the students to find the values. Encourage students to start with the largest coins, then the next largest, ending with pennies. Model a few times either way so that students see that starting with the larger coins is usually much easier. Keep the total values below 50 cents and use no more than 5 pennies in each combination. Remind students to use skip counting and counting on whenever possible. If time permits, have students display combinations of coins for the other students to count. Students can use calculators to check their totals.

Find the Value of Coins in a Bag. Students work in pairs for this activity. Each group has a calculator and a paper bag with about 15 coins in it. Included among the coins should be three to four each of pennies, nickels, dimes, and quarters. See Materials Preparation.

To start the activity, one student reaches into the bag, withdraws three coins, and sets them on the table. Each student then records the names of the coins on the Bag of Coins page in the Student Activity Book and determines the total value of the coins. Remind students to use their 100 Charts in the Student Activity Book Reference section to help them find the value of the coins.

When both students in the pair have found the total value, they check it with the calculator. Encourage students to discuss strategies and to work together to find the correct value when there is a difference of opinion. If a student draws the same collection of coins as has already been drawn, he or she puts the coins back in the bag and redraws.

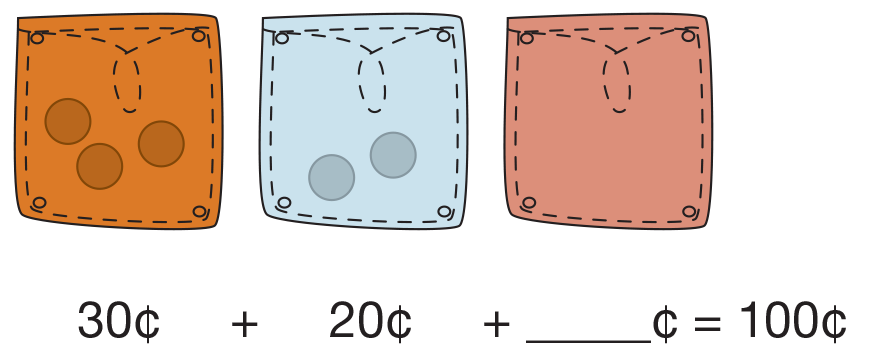
Partition 100¢ into Three Parts. Distribute ten dimes to each student pair and display the Three Pockets Master.

Tell students the story of Joey, Chloe, and Zoey, triplets who share money they get for doing chores. Each day their mom puts dimes in the pockets of two children and they must determine how much money the third child should receive. The dimes equal one dollar each day. Tell students that you are going to place dimes on two of the display pockets and challenge them to find out how much money is in the third pocket.

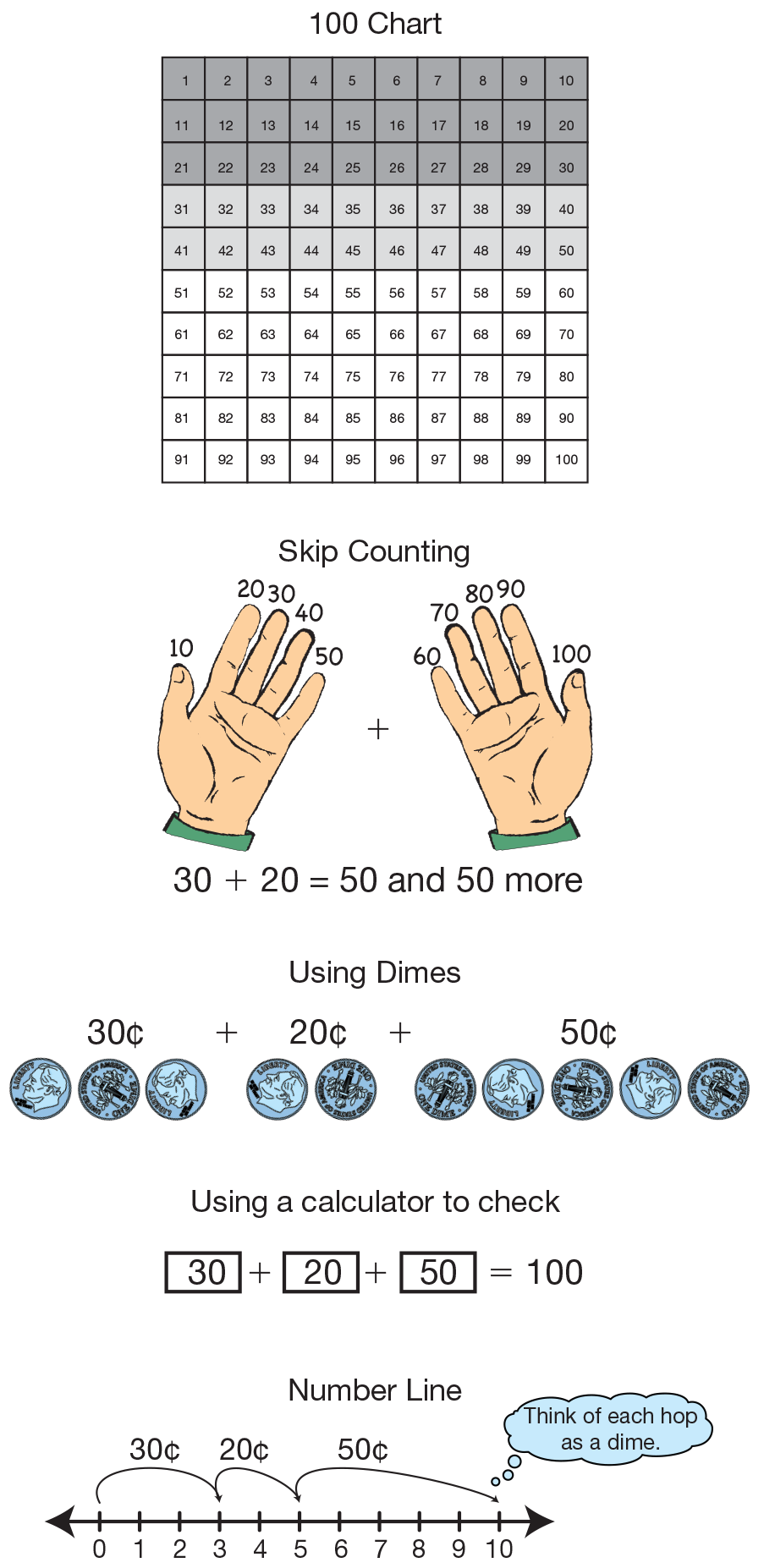
Write the incomplete number sentence below the three pockets then tell students to work the first problem individually. See Figure 5.

When finished, ask volunteers to tell what strategies they used to find the amount of money in the third pocket. Include each of the strategies shown in Figure 6, demonstrating those that students may not have used. After the strategies have been explained, complete the number sentence.

Continue with several more examples randomly alternating the empty pocket.

To provide more practice partitioning 100, assign the Shuttle Bus #100 page in the Student Activity Book. Discuss what the students are being asked to do and make sure they all understand the directions. The encircled tens on the page can be used with counters as a tool in addition to those demonstrated during discussion.