Use Labels. Begin this part of the lesson by directing
students' attention to a display of the Math Practices
page from the Student Activity Book Reference section.
Focus on Math Practices Expectation 6, Use labels.
Tell students that they need to pay careful attention to
labels or units in this lesson. Sometimes they will talk
about coins, either pennies or dimes. At times they will
refer to the value of the coins and they will need to use
the label "cents." Stress that using labels and units
helps to show what numbers mean and will avoid confusion.
See Content Note.

Units. As students say number sentences that describe
the dimes on the ten frame, encourage them to use the proper
unit. If I place 6 dimes on a ten frame, the sentence
60 + 40 = 100 refers to the value of the coins. That is,
60¢ + 40¢= 100¢. If I say 6 + 4 = 10, I am referring to the
number of coins. That is 6 dimes + 4 dimes = 10 dimes.
Making sure that units are consistently labeled in your
discussion with students will help clarify the distinction
between number of dimes and their value.
Connect Representations of Quantities.
Display one dime and ask:
- What is the name of this coin? (dime)
- How much is it worth? (ten cents or ten pennies)
Display the dime and ten pennies and ask:
- Can I buy the same with this dime as I can with these pennies? (yes)
Display the 100 Chart from the Student Activity Book Reference section.
- How many boxes on the chart would you cover to
show one penny? (I would put 1 penny in a box
on the 100 Chart.)
- Which part of the 100 Chart shows one dime? Why?
(10 boxes or one row because it is the same as
10 pennies)
- Place 10 pennies on the chart to show the same as
one dime. [Student places 10 pennies across the
first row of the 100 Chart.]
- If one row is the same as one dime, how many rows
would show 10 dimes? (10 rows)
- How much would ten dimes be worth? (10 tens or
100 cents or one dollar)
- Let's count ten rows of ten cents on the chart.
(10 cents, 20 cents …100 cents.)
Relate Facts to Adding and Subtracting Tens.
Display the Ten Frame page again and place 8 dimes
on it. See
Figure 2.
To emphasize the relationship
between the addition sentence 8 + 2 = 10 and
80 + 20 = 100, ask:
- How many dimes are there? (8)
- How many more dimes are needed to have 10?
(2 dimes)
- What is an addition number sentence that describes this? (8 dimes + 2 dimes = 10 dimes)
- What is the value of all the dimes on the ten
frame? How many cents are 8 dimes worth? How
do you know? (80¢; I can count by tens to 80.)
- How many cents are 2 dimes worth? (20¢)
- What is a number sentence that describes the
value of the coins on the ten frame if we were to
add two more dimes? (80¢ + 20¢ = 100¢)
- What do you notice about these two number sentences?
(In the second number sentence, the
numbers are the same except that there is a zero
at the end. One is dimes, the other is cents.)
- When have we used number sentences like this
before? What did they represent? (We wrote sentences
like that in the links lesson. They showed
the parts of our chain.)
Next place 10 dimes on a ten frame. Then take 3 away. See Figure 3.
Ask questions similar to the following:
- How many dimes did I start with? (10 dimes)
- How many did I take away? (3 dimes)
- How many do I have left? (7 dimes)
- What is the value of the ten dimes? What were the 10 dimes worth? (100¢)
- How much did I take away? What were the 3 dimes worth? (30¢)
- How much do I have left? What are the 7 dimes
worth? How do you know? (70¢; Possible
response:
I skip counted by tens to find the
answer.)
- What number sentence describes the number of
dimes left on this ten frame?
(10 dimes − 3 dimes
= 7 dimes)
- What number sentence describes the amount
of money left on this ten frame?
(100¢ − 30¢ = 70¢)
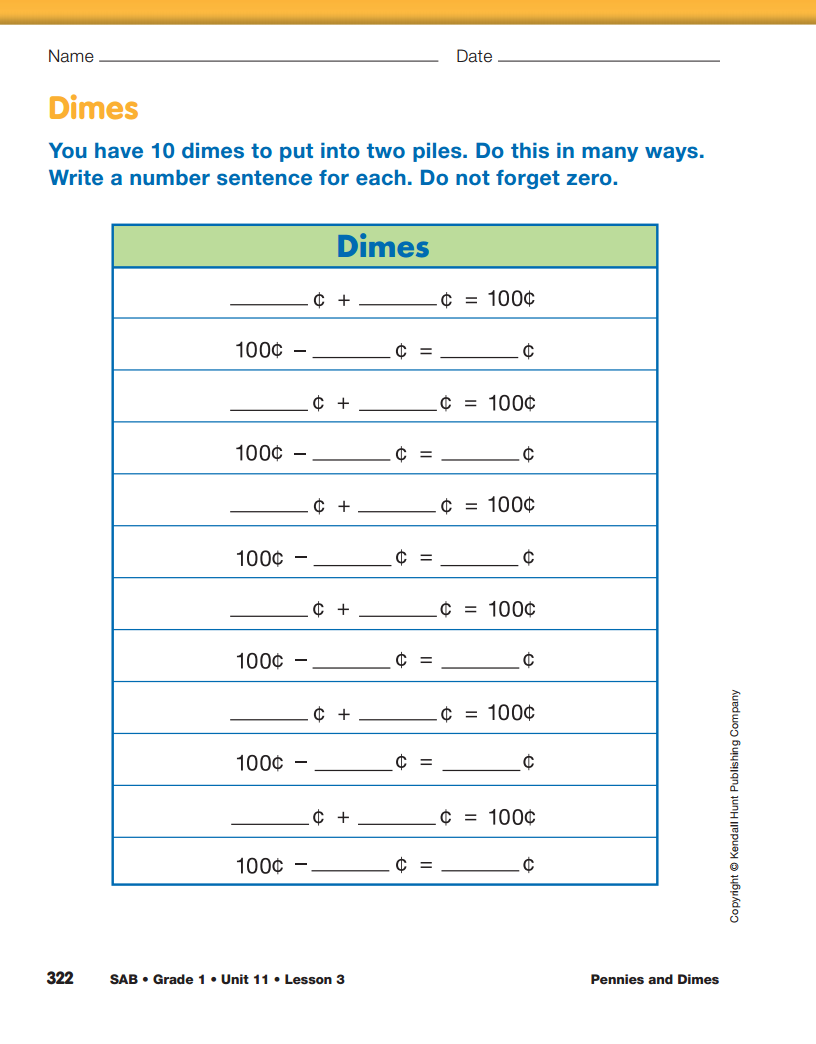
Partition 10 Dimes and Write Number Sentences.
Distribute 10 dimes to each student pair. Ask the pairs
to divide their dimes into two piles. After a few minutes,
ask a student pair to display their partition of the
ten dimes.
- Skip count by tens to count the value of each pile of
dimes. (Responses will vary. Possible response: In
one pile, 10 cents, 20 cents, 30 cents, 40 cents,
50 cents, 60 cents. In the other pile: 10 cents,
20 cents, 30 cents, 40 cents.)
- What is an addition sentence that shows this?
(Possible response: 60¢ + 40¢ = 100¢)
- What is a related subtraction number sentence?
(Possible response: 100¢ − 40¢ = 60¢)
- Is 60 cents the same as 60 dimes? (no)
- Why is it important to use labels like dimes and units
like cents? (Possible responses: so we do not get
confused; 60 cents is not the same as 60 dimes;
without labels, someone might not know what our
numbers mean)
Direct students' attention to the Dimes section on the
Partitioning Pennies and Dimes pages in the Student
Activity Book. Students will work in pairs to find other
partitions of ten dimes by putting them into two piles
in many ways like they did with the pennies. Point out
that in some of the questions on the page they will
write addition number sentences and in others they will
write subtraction sentences to describe the ways they
divided the dimes. Tell students that they are recording
the value of the dimes, not the number of dimes (e.g.,
50¢ + 50¢ = 100¢ not 5 dimes + 5 dimes = 10
dimes). Remind them to think about fact families and
to use the Ten Frames page in the Student Activity
Book Reference section.
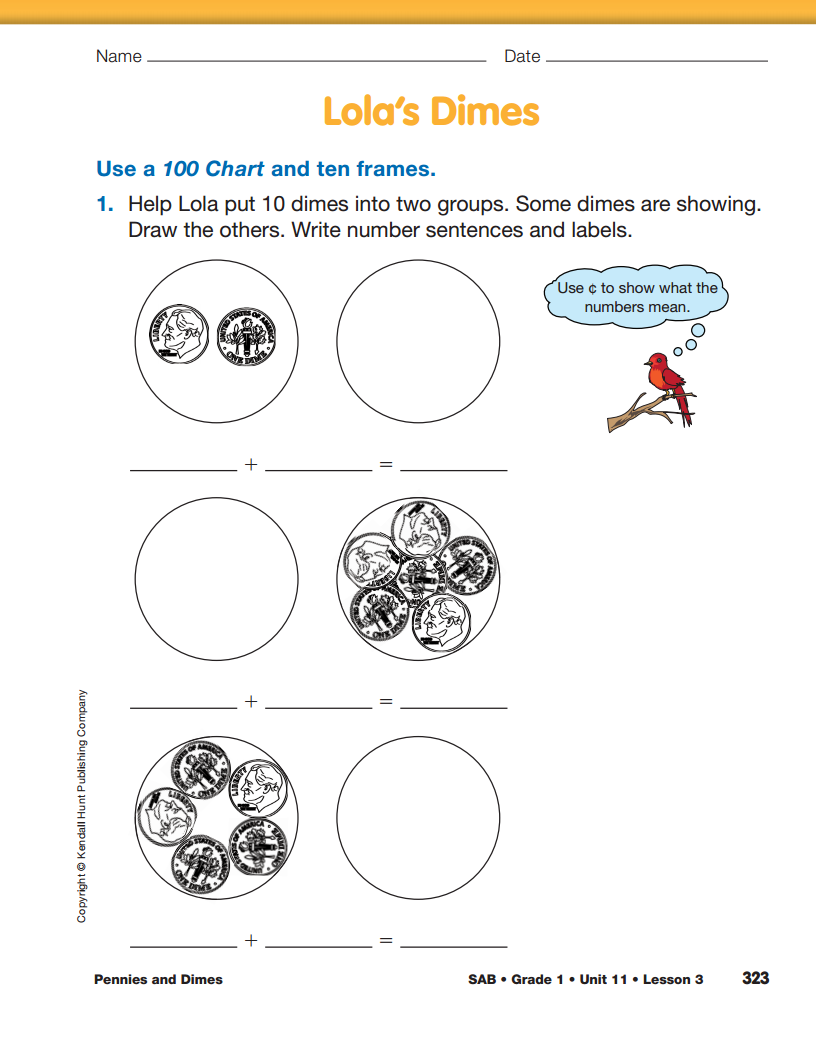
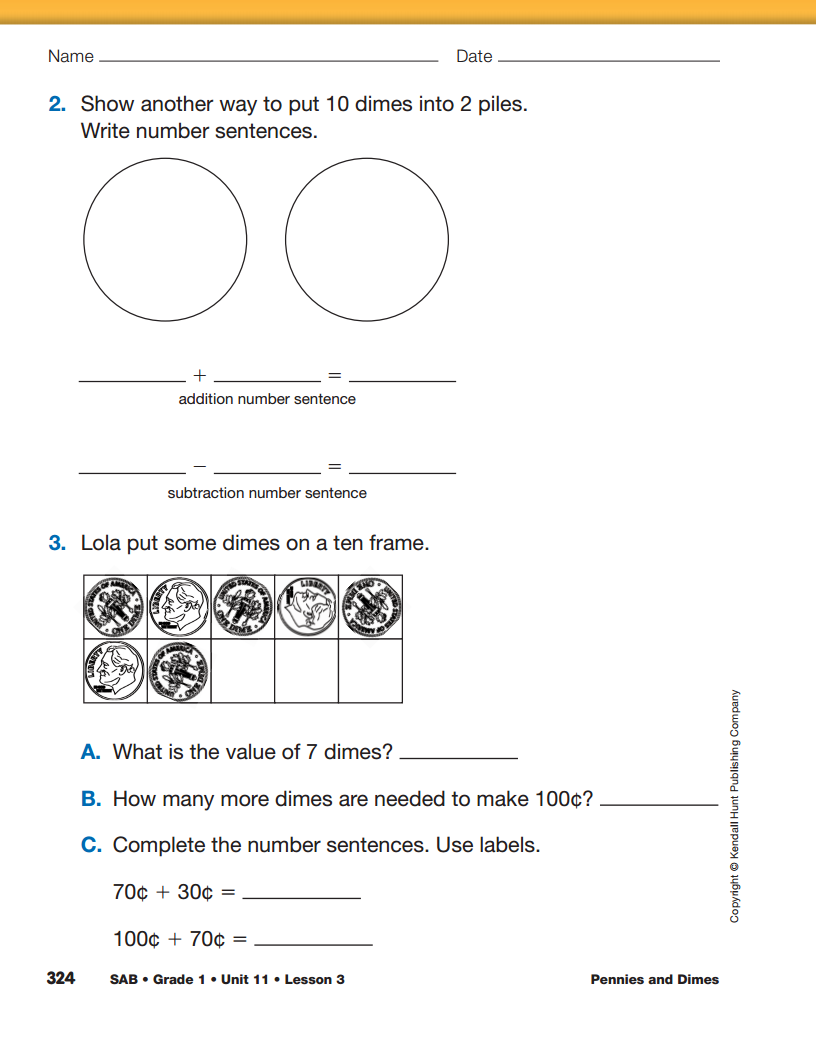
Upon completion, assign Lola's Dimes in the Student
Activity Book to students individually. Students will
use coins and number sentences to represent partitions
of 100.
Use Lola's Dimes with the Feedback Box in the Student
Activity Book to assess students' progress toward partitioning
100 into groups of ten [E1]; representing partitions of
numbers using coins and number sentences [E2];
representing addition and subtraction using number sentences
[E3]; writing numbers to 100 [E4]; solving addition and
subtraction problems involving multiples of ten using coins,
ten frames, and the 100 Chart [E7]; and using labels [MPE6].