Find Simpler Facts. This lesson returns to the break-apart method for solving multiplication problems that students used in Unit 8. After reviewing a few problems that have small factors, students solve multiplication problems in which the factors are more than 10.
Begin by showing students Rectangle A on a display of the Rectangular Arrays page in the Student Activity Book. Students will use their pages as you use the display. Ask students to find the number of small squares in Rectangle A.
- What multiplication problem does this rectangle represent? (7 × 4)
- How do you know? (There are seven rows. Each row has 4 squares.)
- Show or tell how this rectangle can help you solve 7 × 4. (Possible responses: I skip count by rows, 4, 8, 12, etc., until I reach 28; I just know 7 × 4 = 28, but the picture of the rectangle allows me to check my answer by counting squares; I use the break-apart method to make easier products.)
If students don't suggest it, remind them of the break-apart strategy. When using the break-apart method, students are encouraged to break apart the products in ways that provide easier products. The example in Figure 1 shows 7 × 4 and involves a multiple of 5, which is probably easier for most students than the original multiple of 7. Breaking 7 × 4 into 3 × 4 + 4 × 4 might not be much easier.
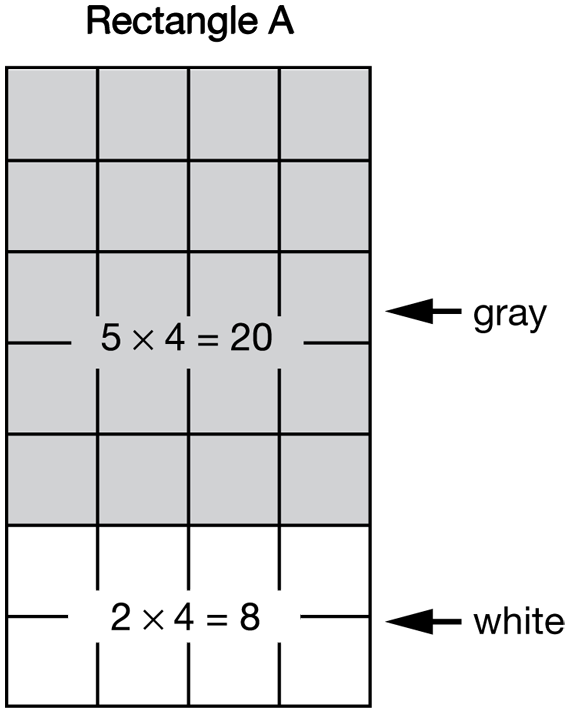
On the display, shade Rectangle A so that a 5 × 4 rectangle is gray and a 2 × 4 rectangle is white as in Figure 1.
- How many square centimeters are in this entire 7 × 4 rectangle? (28 square centimeters)
- How many square centimeters are in the gray region? Include a number sentence. (5 × 4 = 20 square centimeters)
- How many centimeters are in the white region? Include a number sentence. (2 × 4 = 8 square centimeters)
- How did I break the 7 × 4 rectangle apart? (into a 5 × 4 rectangle and a 2 × 4 rectangle)
- How did I break the 7 rows apart? (into 5 rows and 2 rows)
- This picture of Rectangle A shows a way to solve 7 × 4. What is a number sentence that describes that way? 7 × 4 = ? (7 × 4 = 5 × 4 + 2 × 4)
- In 7 × 4 = 5 × 4 + 2 × 4, which numbers show the rows? (5 and 2)
- Why is the 4 repeated in the number sentence? (There are 4 squares in each row of both rectangles.)
Write and solve the number sentence together:
7 × 4 = 5 × 4 + 2 × 4
= 20 + 8
= 28
- Is this a true number sentence? How do you know? (Yes, because both sides of the equal sign make 28.)
- How do the numbers in this sentence match the picture of the rectangle? (7 × 4 shows that there are 7 rows with 4 squares in each row. When you break apart the 7 rows, 5 × 4 shows that there are 5 gray rows of 4 squares. You add them together with the 2 rows of white squares to get 7 rows of 4 squares or 28 squares altogether.)
- How is this strategy helpful? (Possible response: I didn't know 7 × 4, so it breaks 7 into products that are simpler, 5 × 4 and 2 × 4. I already know my 5s and my 2s.)

The Distributive Property. The fundamental property that is involved in breaking apart products is the Distributive Property of Multiplication Over Addition (see the Mathematics in this Unit section of this unit.) Informal understanding of this property is very important for students—it helps them develop facility with mental math and prepares them to understand the traditional multiplication algorithm. However, formal study at this stage is not necessary.
Break a Factor in Half. Many students are comfortable multiplying by 2. Tell students that they can break rectangles into two halves so that they can multiply by 2. Ask a student to draw another 7 × 4 rectangle like Rectangle A on a display of the Centimeter Grid Paper Master. Show students how to carefully count the number of squares on the sides of the drawing of the rectangle so they can be sure that they have an accurate rectangular model with which to work. Tell them that this time they are going to break the other factor, 4, apart.
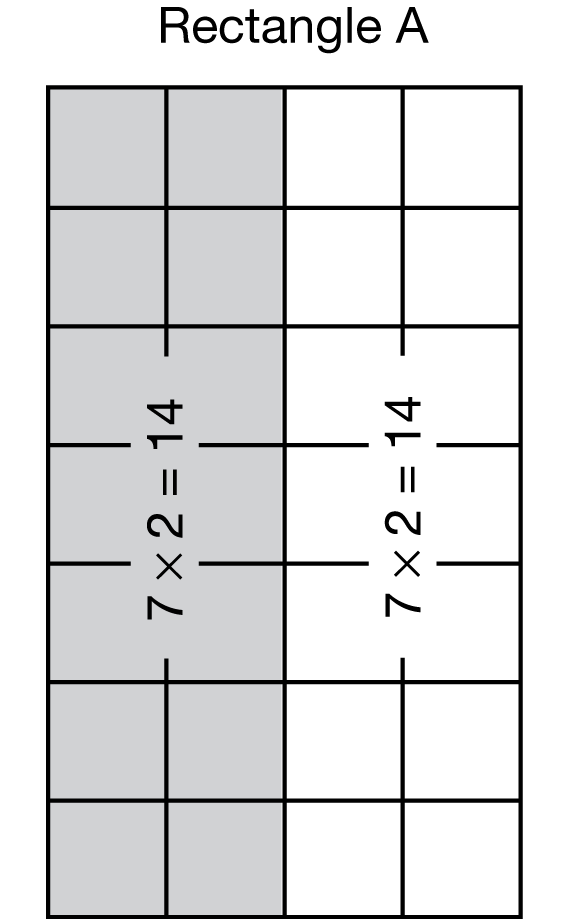
- Show a way to solve 7 × 4 by breaking the 4 into 2 × 2. (The rectangle is broken into two 7 × 2 rectangles. One small rectangle is shaded in. See Figure 2.)
- What number sentence describes the gray half? (7 × 2 = 14)
- What does the 7 represent? (7 rows)
- What does the 2 represent? (the 2 squares in each row of this gray rectangle)
- What number sentence describe the white half? (It is also 7 × 2 = 14.)
- Why are the number sentences the same? (The rectangle is divided into two halves, so each half has exactly the same number of rows and squares.)
- This picture shows another way to solve 7 × 4. What is a number sentence that describes this way? (7 × 4 = 7 × 2 + 7 × 2)
Write and solve the number sentence together:
7 × 4 = 7 × 2 + 7 × 2
= 14 + 14
= 28
- How are the two different number sentences we wrote for Rectangle A alike? Different? (They both show 7 × 4 which is 28. They are different because they show different factors being broken apart.)
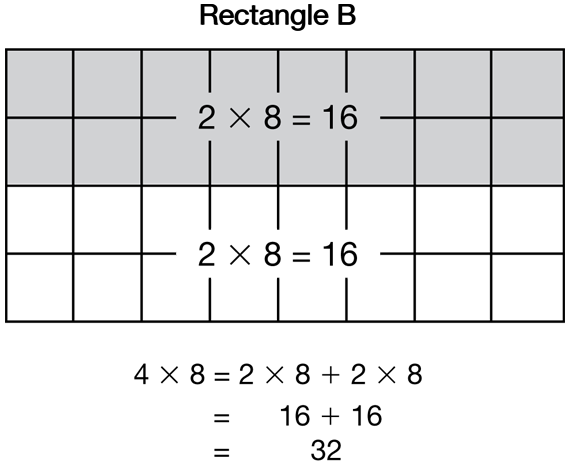
Use Rectangle B on the Rectangular Arrays display to discuss ways to solve 4 × 8. Use questions similar to those you used for the 7 × 4 rectangle, and encourage students to break apart the 4 or the 8 in ways that provide easier products such as 2 × 8 + 2 × 8. See Figure 3.
If breaking apart products into the sum of simpler products is very challenging for students, distribute copies of Centimeter Grid Paper and provide more practice with 4 × 6, 7 × 8, and 8 × 6 rectangles before moving on to larger numbers. Make sure students are making connections between the rectangle pictures and the numbers in the number sentences. Always allow students to use models in these beginning stages of using the distributive property of multiplication over addition to solve multiplication problems.