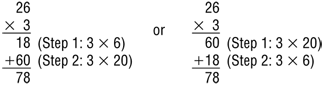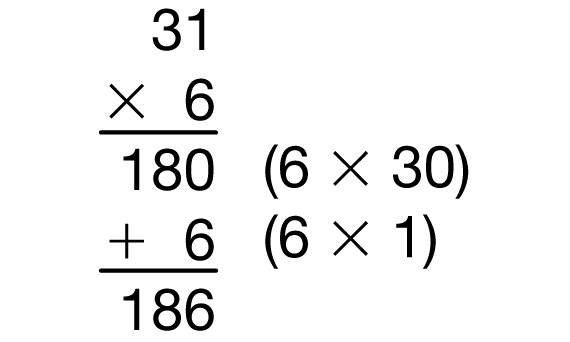Introduce Mara's All-Partials Method. Read the Mara's Way section in the Multiplication Models and Strategies pages. Use Questions 3–5 to guide your discussion. Students are introduced to a paper-and-pencil algorithm for multiplication. The process involves multiplying a factor by the tens and by the ones of the multiplicand. This algorithm, called the all-partials algorithm, allows students to record all partial products. See Figure 3. By having students record all the intermediate products, they should develop a solid understanding of the algorithm. See Content Note about the All-Partials Method.

Why Use the All-Partials Method? To ensure that students have a strong conceptual foundation for the procedures they use to multiply numbers, we introduce the all-partials algorithm. The compact method has more meaning when it is connected to the all-partials method. Without a strong conceptual understanding of multiplication, the compact method could become a series of unintelligible steps. Through all-partials, students build understanding by making connections to place value concepts. While developing paper-and-pencil methods, they use and maintain the conceptual connections among all of the varied strategies and models for multiplication that are introduced.
It is important that students make connections between models and the notations they make.
To broaden this understanding, ask questions such as:
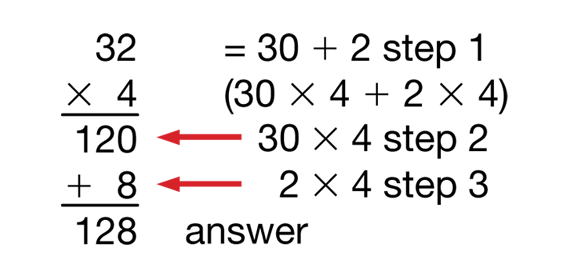
- How did Mara break apart 32? (She broke it into tens and ones, 30 + 2.)
- Why did she write 120? (She multiplied 4 times the 3 tens, or 30, in 32. 4 × 30 = 120.)
- Why did she write 8? (She multiplied 4 times the 2 ones in 32. 4 × 2 = 8.)
- How did she calculate 128? (She added the partial products 120 + 8.)
- How is Mara's way like breaking apart rectangles? Use the display of the 32 × 4 rectangle to explain. (Possible response: Both methods break a product into simpler products. It is like breaking a 32 × 4 rectangle into a 30 × 4 rectangle and a 2 × 4 rectangle. When Mara multiplies the 4 by the tens in 32, that matches the large 4 × 30 rectangle. When Mara multiplies the 4 by the ones in 32, that matches the small 4 × 2 rectangle.)
Ask similar questions about Richard's solution to 26 × 3. The order in which partial products are recorded in the all-partials algorithm does not change the answer. See Content Note about the order of the products. Tell students to use this method to solve 26 × 3 again, but this time to multiply 3 × 20 first.
Order. Changing the order in which the partial products are recorded in the all-partials algorithm does not change the answer. For example, when multiplying 26 × 3, one can record the 18 before the 60:
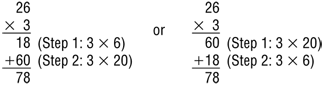
- Did you get the same answer as Richard?
- Does it matter if you multiply the 4 by the ones or by the tens first? (No, the order you multiply does not matter. It does not change the product.)
Jason records his work with partial products a different way.
- How is Jason's way of recording his work like Richard's way? (Possible response: Jason breaks the 26 into tens and ones, 20 + 6, like Richard does. Then he records partial products like Richard does. He multiplies the tens times 3, 20 × 3, and records 60. He multiplies the ones times 3, 6 × 3, and records 18. They both add the partial products, 60 + 18, to get the same product, 78.)
- How is Jason's way different from Richard's? (Possible response: It looks different. Richard's problem is recorded in a vertical fashion. Jason's problems are written side by side. Jason multiplied 20 × 3 first. Richard multiplied 6 × 3 first.)
Connect Models to the All-Partials Method. Show a display of the Rectangle Models Master. Direct students' attention to Rectangle A.
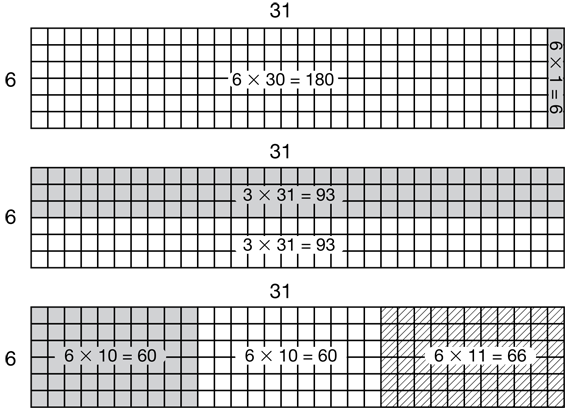
- What is a quick way to estimate the number of squares in Rectangle A? (Possible response: Multiply 6 times 30 for an estimate of 180.)
- Talk with a partner about the ways to divide Rectangle A into parts. (See Figure 4.)
- Which way to break Rectangle A apart makes it easiest to find the answer? Why? (Possible response: Breaking 31 into 30 × 1 makes it easy to find the answer. Breaking a factor so one of its parts is a multiple of 10 helps since it is easy to multiply by tens.)
- Break Rectangle A into tens and ones to solve 31 × 6. (30 × 6 + 1 × 6 = 180 + 6; 180 + 6 = 186. See first rectangle in Figure 4.)
- Instead of using a rectangle, use Mara's method to solve 31 × 6. (See Figure 5.)
- How do the parts of the rectangle match with the numbers you recorded when you used Mara's method? (Possible response: 1 × 6 matches with the small rectangle that has 1 square in each of the 6 rows. I multiplied 1 × 6 and wrote down 6. 30 × 6 matches with the larger rectangle that has 30 squares in each of 6 rows. I multiplied 30 × 6 and wrote down 180. 6 + 180 = 186 which is the total number of squares in the rectangle.)
- Is your answer reasonable? How do you know? (Possible response: My answer is reasonable because it is close to the estimate of 6 × 30 = 180.)
It is important that students check whether their answers are reasonable after any paper-and-pencil or calculator calculation. Sometimes, computed answers are ridiculously incorrect and a simple mental estimate will catch the error. Students should develop the important habit of checking whether their answers make sense. They can do a quick estimate before solving the problem, or solve the problem a second way to check their answer.
Display Rectangles B and C of the Rectangle Models Master. Continue making connections to the models while practicing the all-partials method. Have student volunteers break apart the rectangles by tens and ones while the others are solving the problems using Mara's all-partials method. Use prompts similar to those for Rectangle A so that students estimate, make connections between the rectangle models and the all-partials notation, and check to see if their answers are reasonable.
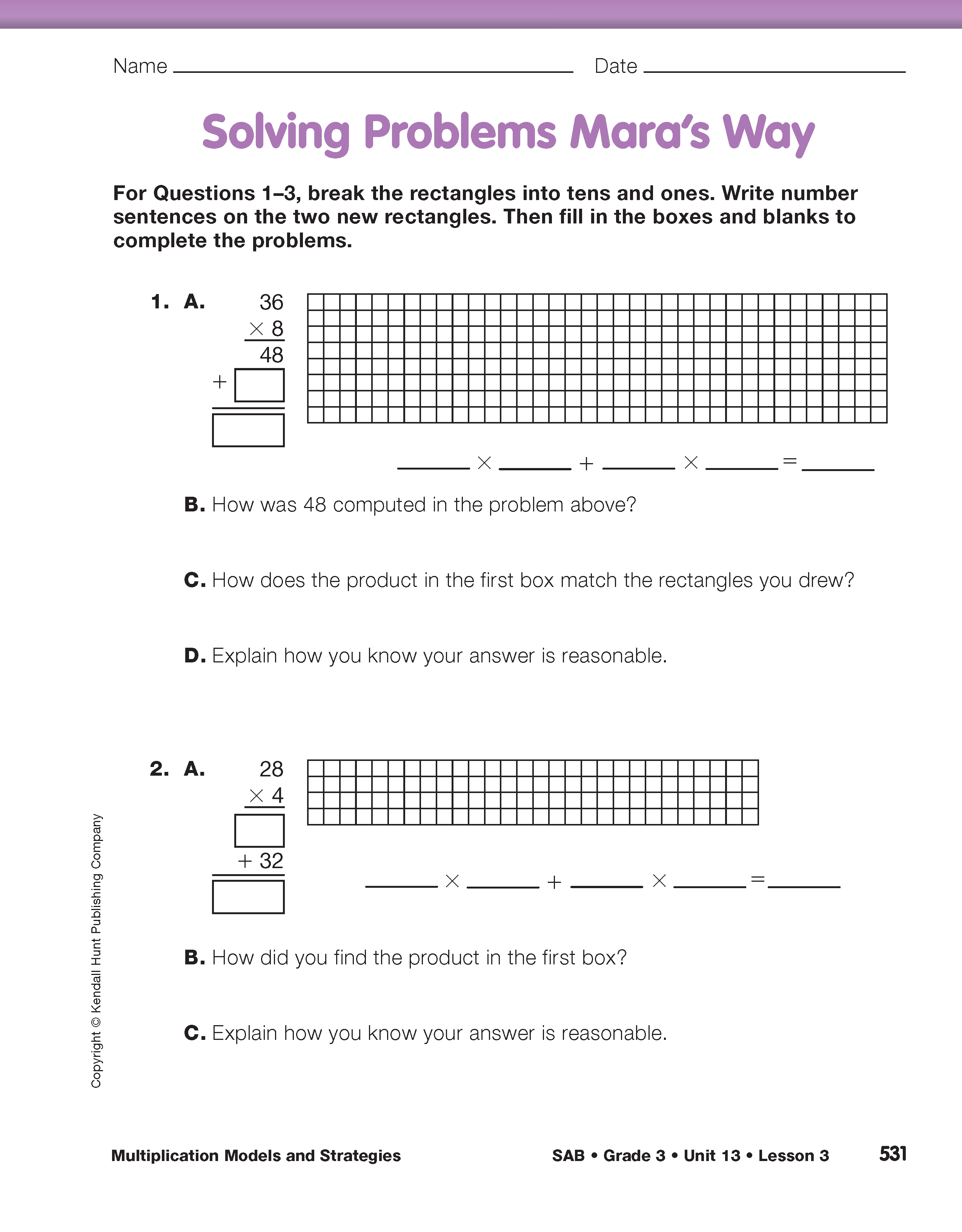
Assign the questions on the Solving Problems Mara's Way pages in the Student Activity Book. Students will practice using the all-partials method to solve 2-digit by 1-digit multiplication problems.
As students work on Questions 1–8, monitor their work. Help students find ways to divide rectangles to make multiplication easier. Make sure they understand the meaning behind the notations they make.
To check for understanding ask:
- Can you estimate this product?
- How did you calculate this number?
- What would the two rectangles that match this problem look like?
- What number sentences describe these rectangles?
- Match the numbers in the number sentences with the rows and squares in the rows of the rectangles.
- How do you know that this answer is reasonable?
Provide copies of the Half-Centimeter Grid Paper Master for students who need the support of the grid to make their sketches in Questions 4–8.

Use Check-In: Questions 3–8 on Solving Problems Mara's Way in the Student Activity Book to assess students' progress toward the following Expectations:
- Represent 2-digit by 1-digit multiplication problems using rectangular arrays and number sentences [E1].
- Show connections between models and strategies for multiplication [E2].
- Solve multidigit multiplication problems using mental math strategies (e.g., decomposing numbers) [E3].
- Multiply one-digit whole numbers by multiples of ten [E5].
- Solve multiplication problems by breaking products into the sum of simpler products using a rectangle model and the paper-and-pencil all-partials method [E7].
Use Check-In: Questions 3–8 to also assess students' abilities to check the reasonableness of their solutions [MPE3].
Ask students to use Roberto's Chart Master from Lesson 2 and Half-Centimeter Grid Paper to write multiplication stories and to represent the stories and solutions with rectangular arrays to provide targeted practice with these Expectations.