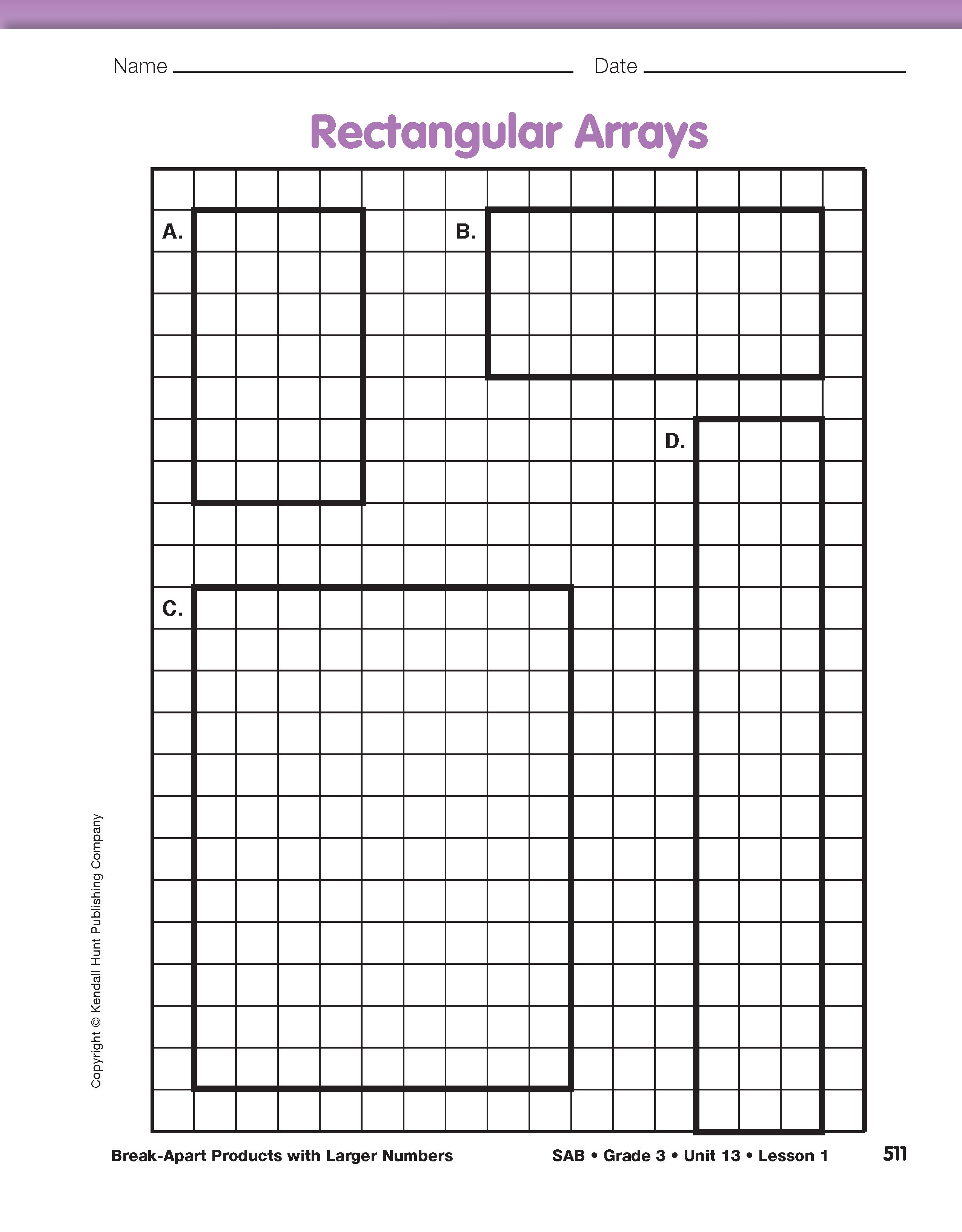
Break into Tens and Ones. Continue displaying the page and direct students' attention to Rectangles C and D on the Rectangular Arrays page in the Student Activity Book.
- How are these rectangles different from Rectangles A and B? (They are bigger.)
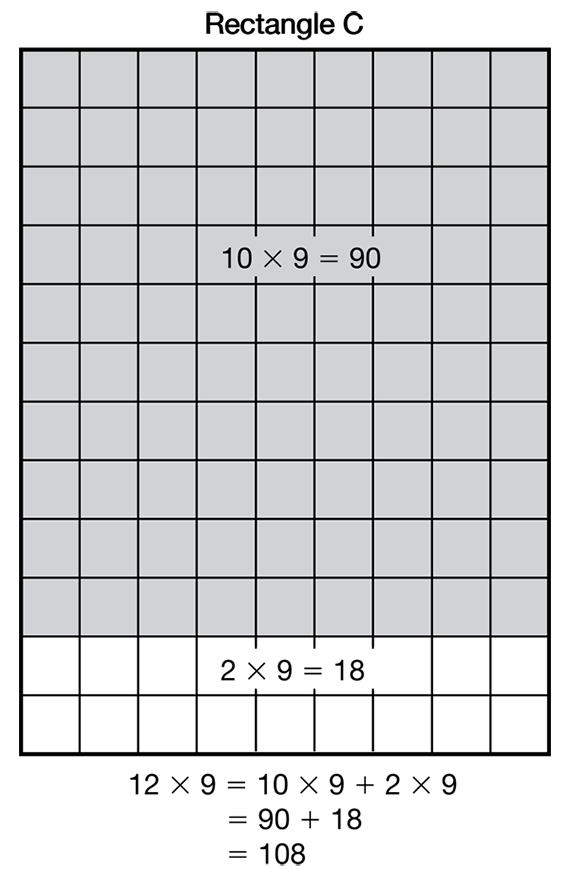
- What multiplication problem does Rectangle c represent? (12 × 9)
- How do you know? (There are 12 rows, and each row has 9 squares in it.)
Tell students that products that have at least one factor between 10 and 20, such as the problems associated with Rectangles C and D, can be broken apart so that one of the easier products involves 10.
- Are you comfortable multiplying by 10? (Responses will vary.)
- What pattern helps you remember the facts for the 10s? (Possible responses: All multiples of 10 end in zero. When I multiply a number by 10, the product is that number and a zero after it.)
- Show how you can break apart Rectangle C so that one of the sides of a new rectangle is 10. (Make a 10 × 9 rectangle and a 2 × 9 rectangle.)
- Write a number sentence that describes that way. (12 × 9 = 10 × 9 + 2 × 9; See Figure 4.)
Write and solve the number sentence together, asking students to make connections between the rectangle picture and the numbers in the sentences.
12 × 9 = 10 × 9 + 2 × 9
= 90 + 18
= 108
- Look at the number sentence. What does the 10 represent? (10 rows in the 10 × 9 rectangle)
- What does the 2 represent? (2 rows in the 2 × 9 rectangle)
- How are the 12 and the 10 and the 2 related in this number sentence? (The 12 is the number we broke apart into 10 + 2)
- What do the nines represent? (There are 9 square centimeters in every row.)
- Why is 9 repeated in the number sentence? Use the rectangle drawing to explain. (We broke the large rectangle into two smaller rectangles, a 10 × 9 and a 2 × 9. The 9 is repeated because there are 9 square centimeters in each row of each smaller rectangle. We do not break the 9 apart in 12 × 9.)
- Explain how you can check this answer. (Possible response: For the 10 × 9 rectangle, I can skip count by 10s to find 90. I know 2 × 9 = 18. 90 × 18 = 108.)
- Which is easier to solve, 12 × 9 or 10 × 9 + 2 × 9? (Answers will vary. Possible response: It is easier for me to multiply by 10 and multiply by 2 instead of multiplying by 12.)
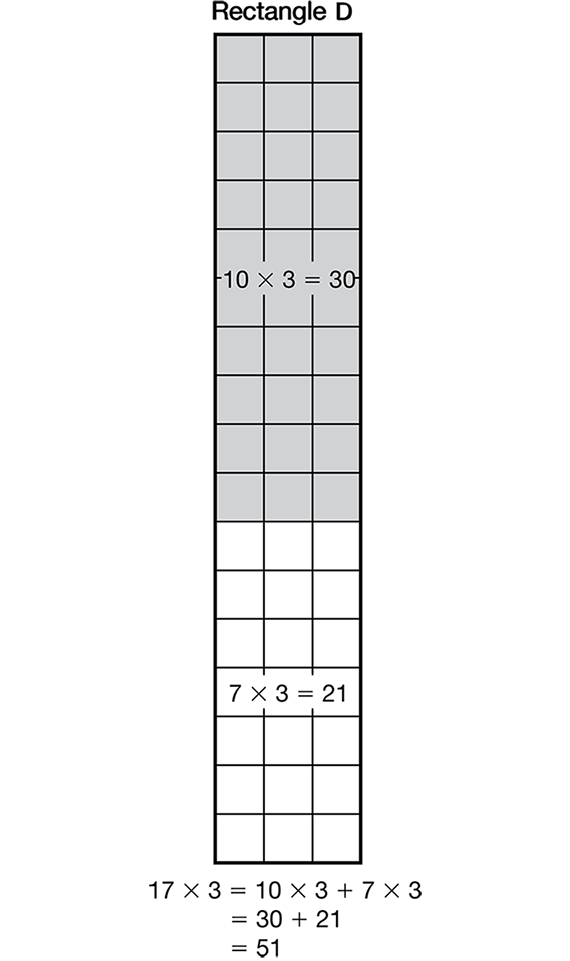
For Rectangle D, students can break apart the product in this way: 17 × 3 = 10 × 3 + 7 × 3. Again, point out that it is helpful to break numbers into products that are easier, into tens for example. Breaking 17 × 3 into 13 × 3 + 4 × 3 is correct but probably not any easier to solve. See Figure 5.
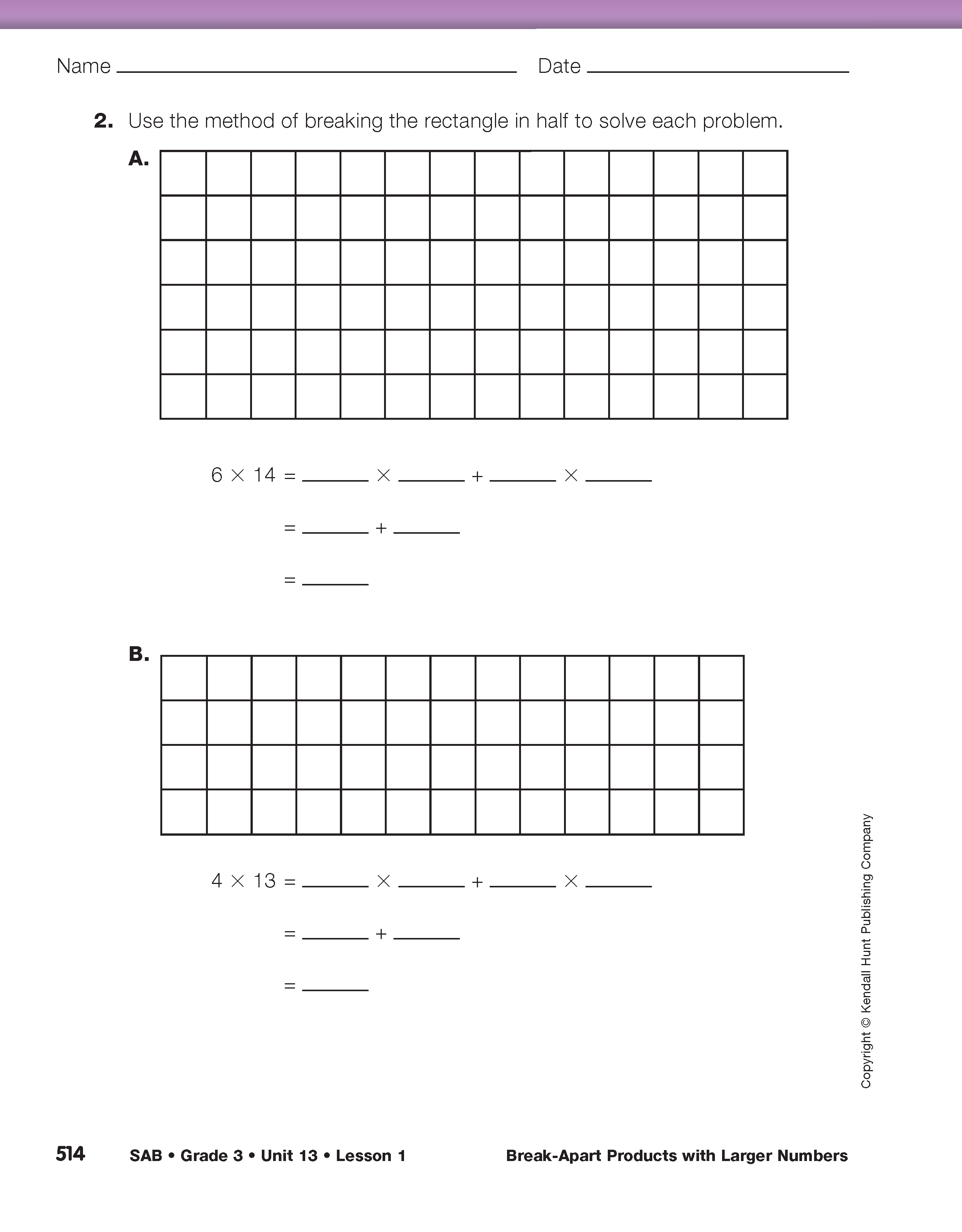
Practice the Break-Apart Method. Direct students' attention to the Break-Apart Products with Larger Numbers pages in the Student Guide. Read the vignettes together. Students first review the break-apart method with smaller numbers, 7 × 6. Then they review the method with larger numbers, breaking products into tens and ones and halving.
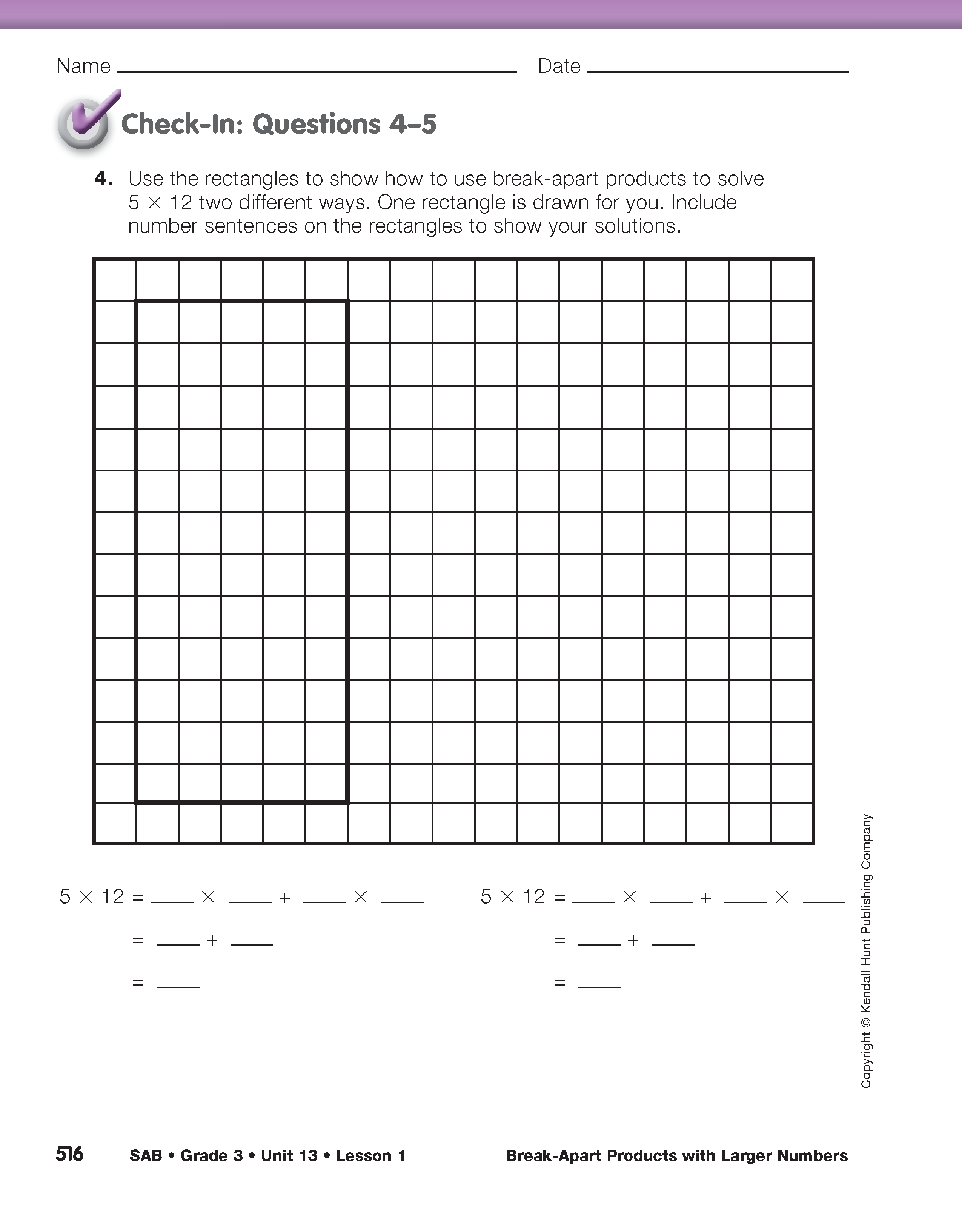
After reading the vignette, assign Questions 1–5 on the Break Apart and Multiply pages in the Student Activity Book. Students will practice using all partials first by breaking the products apart as in Rosa's method. Question 2 provides practice using Mark's method of a breaking a product in half. In Question 4 students are asked to draw a 5 × 12 rectangle. Remind them to carefully draw and then count the number of squares on the sides of their rectangle so that they have an accurate rectangular model with which to work.

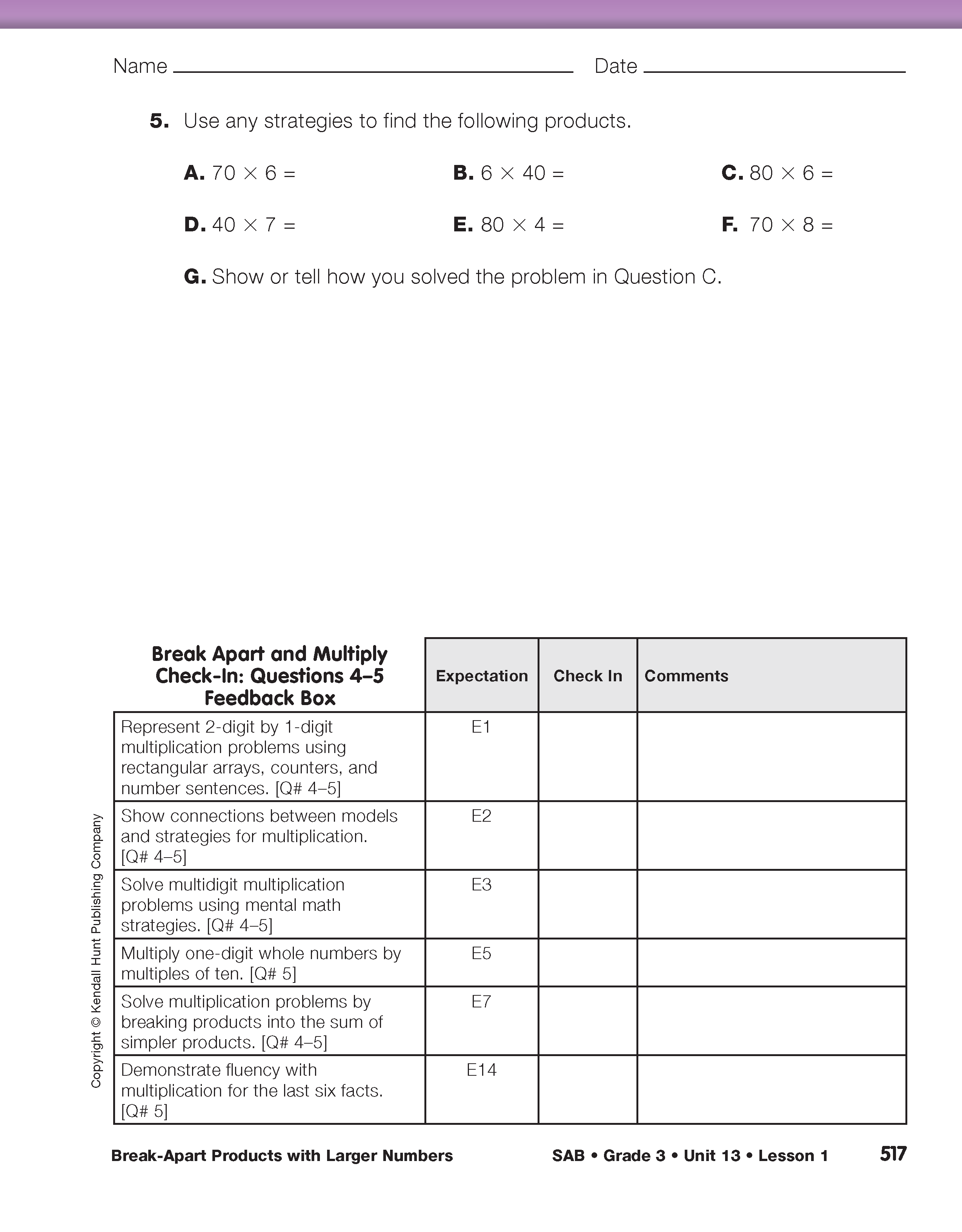
Use Check-In: Questions 4–5 on the Break Apart and Multiply pages in the Student Activity Book to assess students' abilities toward the following Expectations:
- Represent 2-digit by 1-digit multiplication problems using rectangular arrays and number sentences [E1].
- Demonstrate partial products using a rectangle model for multiplication [E2].
- Solve multidigit multiplication problems using strategies (decomposing numbers and halving) [E3].
- Multiply one-digit whole numbers by multiples of ten [E5].
- Solve multiplication problems by breaking products into the sum of simpler products (applying the distributive property of multiplication over addition) using a rectangle model [E7].
- Demonstrate fluency with multiplication for the last six facts [E14].