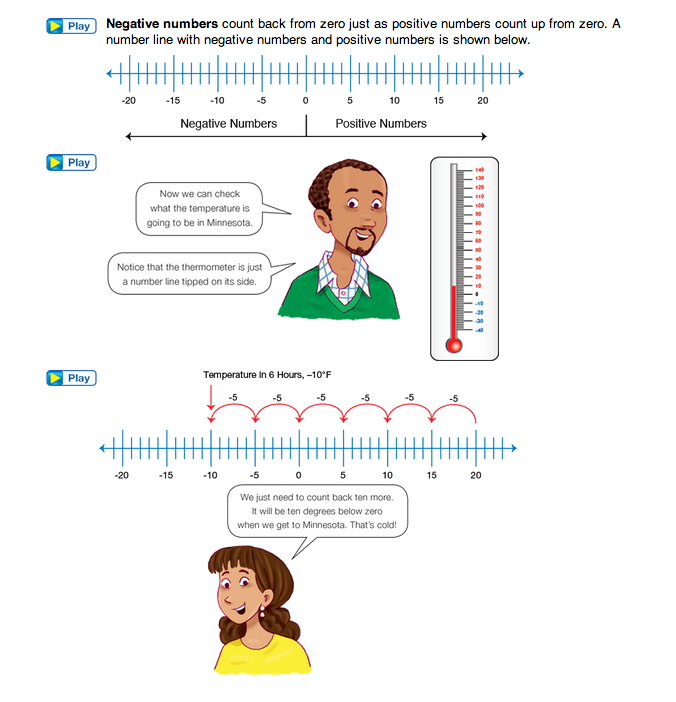
Introduce Negative Numbers. Instruct students to read the first page of the opening vignette on the What's Below Zero pages in the Student Guide for an introduction to negative numbers. Here, Professor Peabody, Tom, and Rhonda travel to Minnesota and want to know what the temperature will be when they arrive.
Scales to Measure Temperature. The F on the thermometer shows the temperature measured using the Fahrenheit Scale. On this scale, water freezes at 32°F and boils at 212°F. This system is usually used in the U.S. The Celsius Scale is used in many countries of the world. On the Celsius Scale, water freezes at 0°C and boils at 100°C.
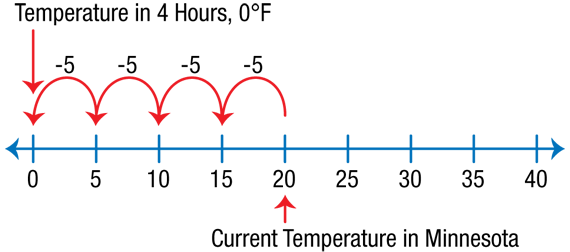
- In Minnesota the current temperature is 20°F. The temperature will drop 5 degrees per hour. What will the temperature be in six hours? (The temperature will be −10°F.)
- Show or tell how you know. (Possible response: I thought about the number line. In 4 hours the temperature will be at 0°F. After 2 more hours the temperature will drop 10 more degrees. The temperature is at −10°F.)
Students might suggest skip counting backward, subtracting five 6 times, using a calculator, or using a thermometer. Gather a few different solutions on a display.
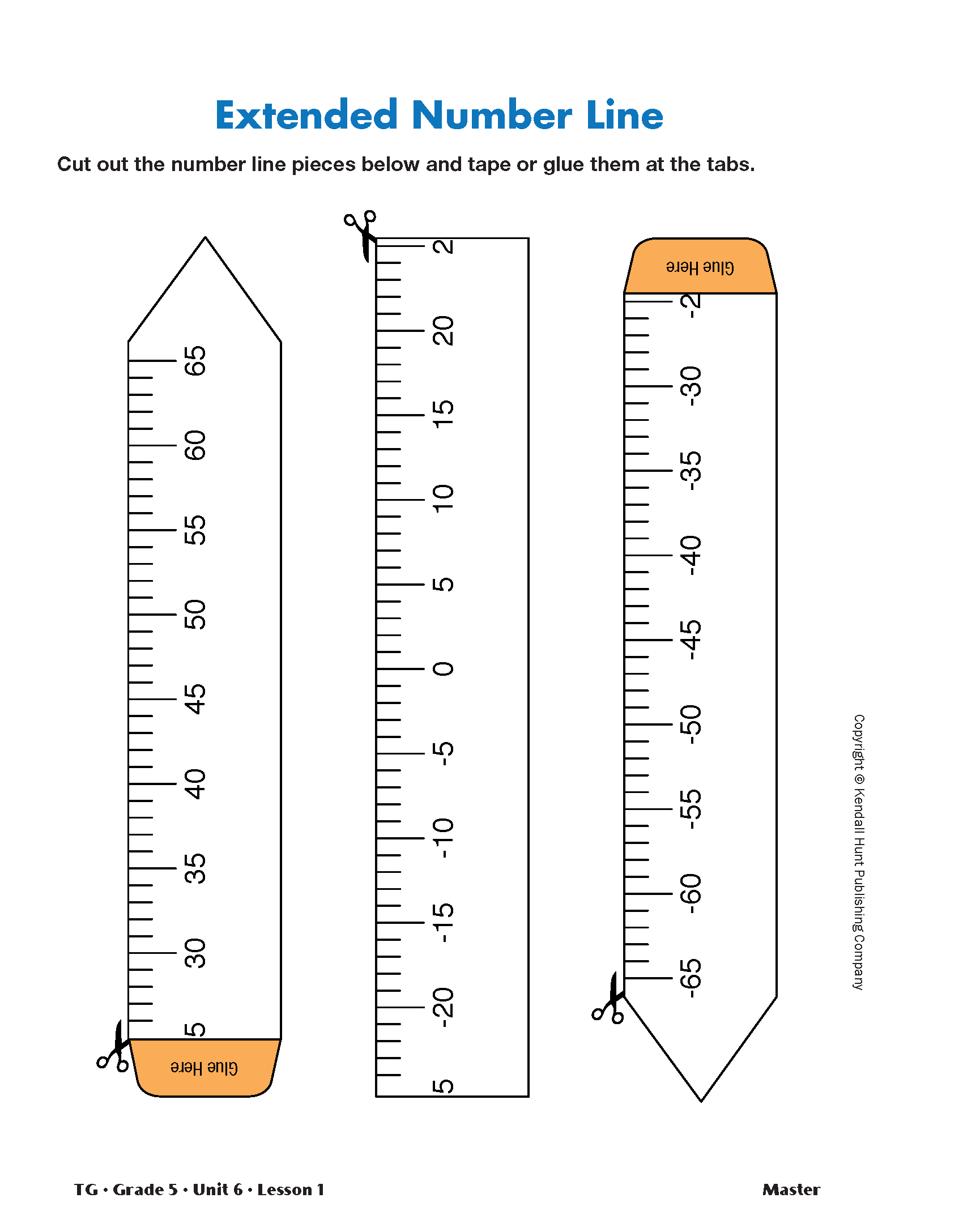
Make Extended Number Lines. Show students how they can solve the problem using a number line. Have students cut out and assemble the number line from the Extended Number Line Master. Students can then model the problem on the number line. Display the number line.
- Where is 20°F on the number line?
Mark 20 on the number line.
- If the temperature drops, in what direction would you move on the number line? (Move left in a negative direction.)
- How will you find the temperature in 1 hour? (Move 5°F to the left on the number line.)
Make a five-degree hop to the left along the number line to show the temperature drop in one hour to 15°F.
- What will the temperature be in 2 hours? 3 hours? 4 hours? How do you know?
Show the temperature changes by hops of 5 on the number line on the display as students continue to demonstrate the temperature drops until reaching 0.
Continue reading the rest of the vignette in the Student Guide as Rhonda and Tom discuss extending and using the number line to solve the problem.
Some students may be confused as the numbers head below zero while others may already be familiar with thermometers and temperatures below zero. Remind students that any number to the left of 0 becomes a negative number, or “below zero” since we are talking about temperatures and thermometers.
Ask students to locate various temperatures on a display of the Extended Number Line.
- What will the temperature be in 5 hours? (–5°F)
- What will the temperature be in 6 hours? (–10°F)
To avoid confusion with changes in temperature and with adding or subtracting negative numbers, discuss changes in temperature using the terms rise and drop.
Solve Problems with Negative Numbers. Ask student pairs to discuss and answer Questions 1–5 in the Student Guide. After most students have had a chance to answer these questions, ask students to share solution strategies for each problem. Have a display of the Extended Number Line readily available.
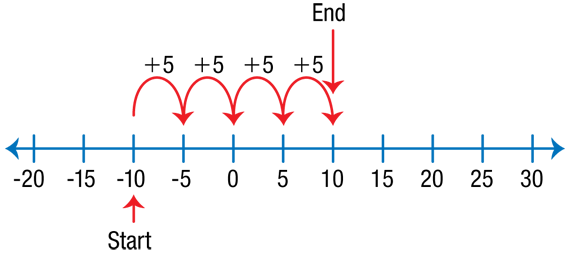
- How did you solve Question 1? (Possible response: First I started at –10°F on the number line, then hopped to the right 20°F since it was getting warmer. I ended up at 10°F.) [See Figure 2.]
- Did someone solve the problem another way? (Possible response: I used a calculator: −10 + 5 + 5 + 5 + 5 = 10.)
- How did you enter the negative 10? (Possible response: I used the +/− or “change sign” key on the calculator.)
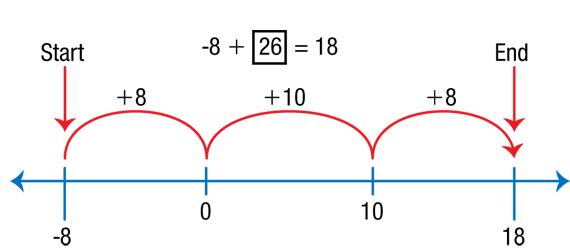
- How did you use the number line to solve Question 2? (Possible response: I put a mark on the number line at –12°F to start and then counted up 24; I counted 12 to get to 0 and 12 more to reach 12°.) [See Figure 3.]
- How is Question 3 different from Questions 1–2? (Possible response: In Question 3, I am trying to find the change or difference in temperature rather than the ending temperature.)
- How did you use the number line to solve Question 3? (Possible response: I located the starting temperature and ending temperature and counted the degrees between.) [See Figure 4.]
- Joe Smart thought the answer would be 10 because, looking at his two marks on the number line, 18 − 8 = 10. Is his response reasonable? (Possible response: No, because the temperature started at −8°, which means it must rise 8° just to reach 0, and 2 more degrees won't get him near the 18 degree mark.)
In Question 4, students determine the amount of temperature change from a positive temperature to a negative temperature on the thermometer. Have a student demonstrate on the number line how to show the solution to the problem.
- Where did you start on the number line for Question 4? (5°F).
- Did the temperature rise or fall/drop? (The temperature fell.)
- Show on the number line what you did next. (Possible response: I put a mark at 5°F, then I counted to the left [negative direction] by 11 degrees. 5 hops to reach 0, then 6 more hops to make an 11-degree change. I landed on –6°F.)
- In which direction did you hop on the number line? (I hopped to the left because the temperature dropped or fell.)
In Question 5, students determine the amount of temperature change between two negative temperatures.
- Show how to use a number line to solve Question 5. (Possible response: I started at −20 and made a mark on the number line, then I made another mark at –3°. I counted the hops from −20 to –3 and got 17, so the temperature must rise 17°F to reach −3 degrees on the thermometer.)
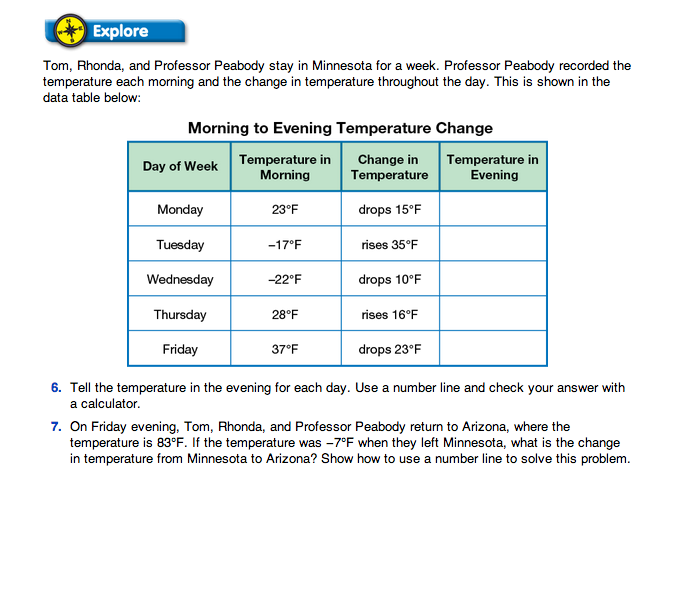
Direct students' attention to the Explore section in the Student Guide. Read the opening vignette that describes how Professor Peabody created a data table to record the temperature each morning and the changes in temperature throughout the day. In Question 6, students must determine the evening temperatures for each day using the number line.
- If a temperature drops, in what direction would you move on the number line? (Possible response: to the left)
- Is the temperature getting warmer or colder? (colder)
- What is the starting temperature on Monday morning? (23°F)
Ask students to work with a partner to discuss and answer Questions 6–7. While students are working, circulate and ask students to clarify and describe their thinking.
- Show how to use the number line to solve this problem.
- Where do you mark your starting temperature on the number line?
- Where do you mark your ending temperature on the number line?
- What is the difference between the two temperatures?
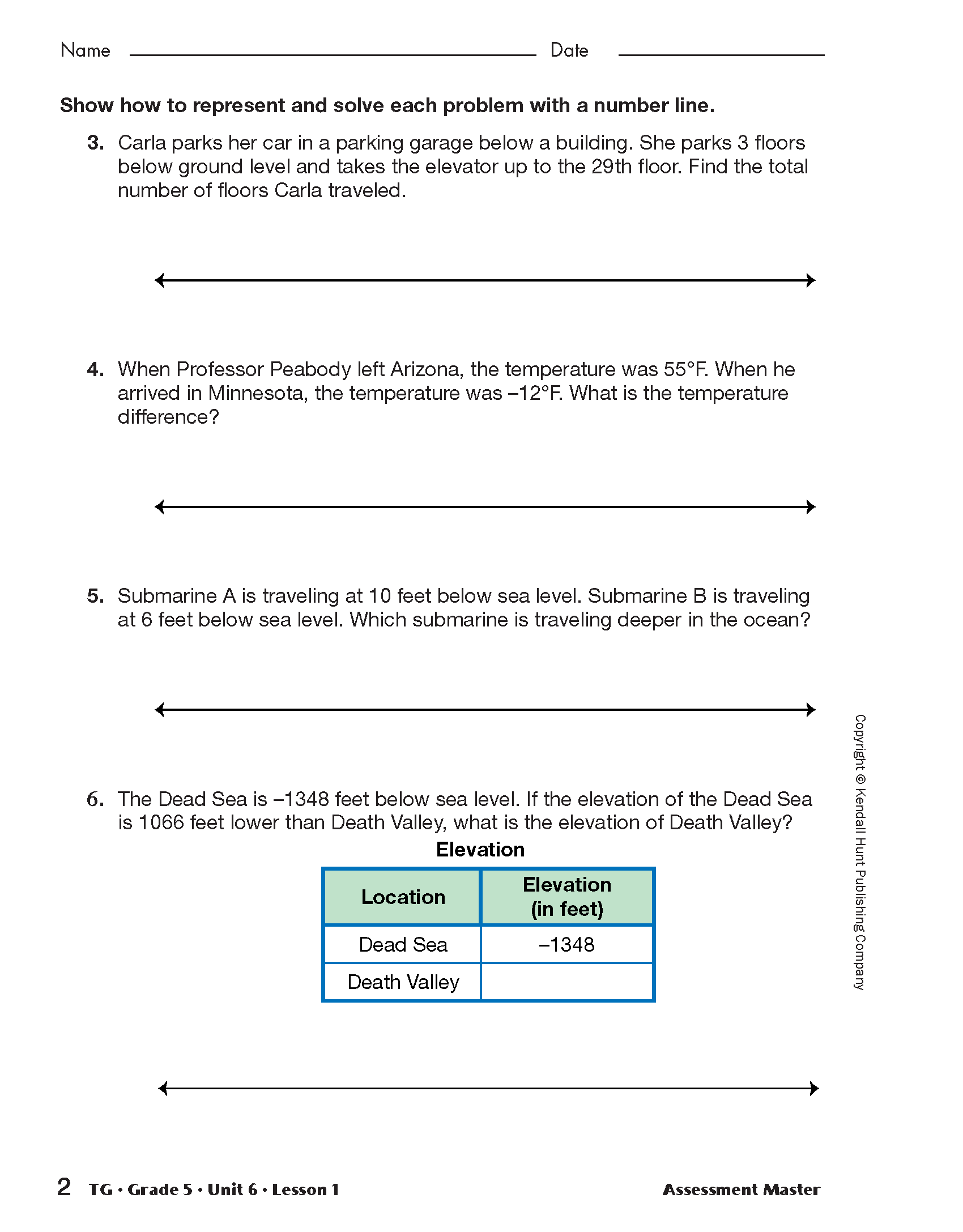
Assign the Professor Peabody Made a Mess Assessment Masters to assess students' abilities to represent negative numbers on a number line and solve problems with negative numbers. Students should work individually on this activity.
Use the Professor Peabody Made a Mess Assessment Masters to assess students' abilities to represent negative numbers on a number line [E1]; use number lines to solve problems with negative numbers [E2]; and show work [MPE5].
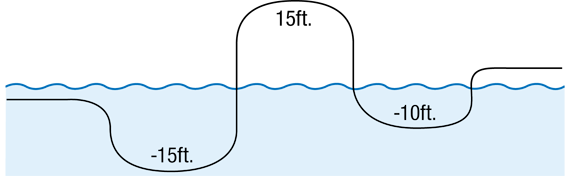
Elevation. Elevation is measured in relation to sea level. A negative is used to indicate below sea level. See Figure 5.