Define and Sort Polygons. Display the first page of the Student Guide. This page describes Professor Peabody's dream about a town called Flatopia, where all of the creatures are polygons. Students might recall that they read about Professor Peabody's journey to Flatopia in a story in Grade 4. To help Professor Peabody organize the Flatopia Polygon Zoo, students must decide on ways to sort and classify the Shapes Zoo Pieces in the Student Activity Book.
To start, students need to determine if all the shapes are polygons. Refer students to the shapes above Question 1. Ask students to look at the shapes and to discuss Question 1 with a partner.
As students are talking, circulate and ask:
- Why is [Shape 3] a polygon? (Possible response: It is a shape with straight sides.)
- Why is [Shape 9] not a polygon? It has straight sides. (Possible response: The sides cross; the shape really has 6 sides and too many vertices touch in the middle.)
- Why is [Shape 7] not a polygon? (Possible response: it does not have straight sides that meet at the corners.)
Have several students share their definitions with the class.
Invite responses to each definition presented.
- Does your definition include Shape 8? This is not a polygon. (Possible response: I need to change my definition. The shape is not closed and is not a polygon. A polygon must be a closed shape.)
- Does Shape 2 fit your definition? (Possible response: It is a closed shape with straight sides and only two sides meet at each corner.)
- Draw another shape that is a polygon. Does this shape fit your definition?
- Draw another shape that is not a polygon. Why is this shape not a polygon?
Polygon. A polygon is a two-dimensional connected figure made of line segments in which each endpoint of every side meets with an endpoint of exactly one other side. Ask students to work with a partner to write down a definition of polygons they can agree on.
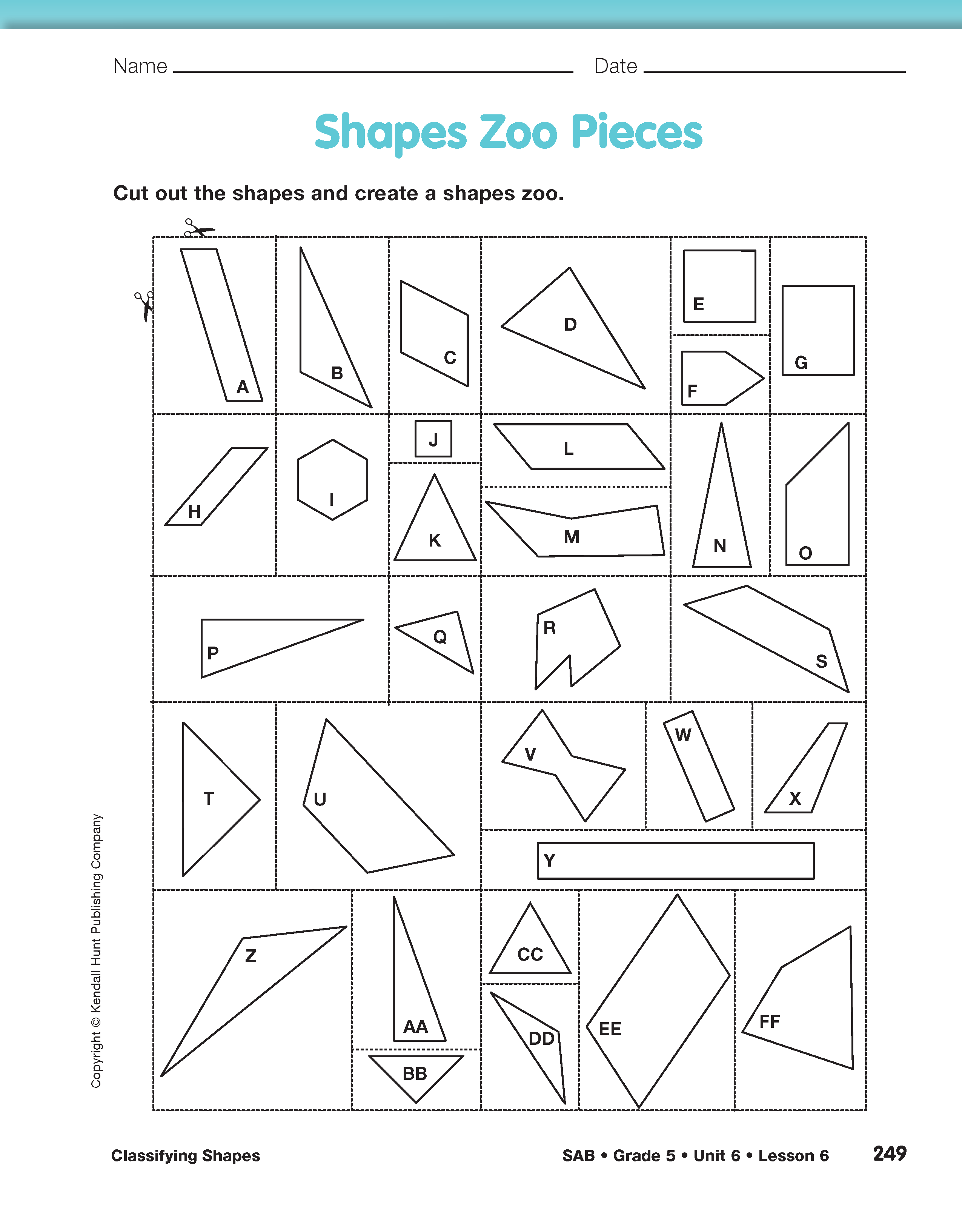
In Question 2, students sort the Shapes Zoo Pieces into two piles: polygons and shapes that are not polygons. Give each student scissors, tape, and a large piece of paper. Students will draw the shape zoo on the paper as the lesson progresses. For now simply have students sort the shapes.
- Is Shape V a polygon? (yes) How do you know? (It has straight sides, two sides meet at each corner, and the shape is closed.)
- Look at the shape you drew that is not a polygon. Are any of the Shapes Zoo Pieces not polygons? (No, all the shapes are polygons.)
- What should Professor Peabody do with the shapes that are not polygons? (Possible response: Find a new home for them. Only polygons can go into the polygon zoo.)
- How should Professor Peabody organize the shapes in the zoo? (Possible response: I think he needs to put similar shapes together just like a zoo. For example, I think the shapes with three sides should go together.)

Complete mastery of the concept of classification of shapes and of giving a precise definition for a kind of shape can only be expected of students at higher van Hiele levels. For example, students at van Hiele level 0 (visualization) will have difficulty with a question that asks if every square is a rectangle. However, grappling with these ideas helps students move to higher cognitive levels.
Ask students to read Question 3.
- Do you think this is a good way to sort the shapes?
- What is a quadrilateral? (Possible response: A quadrilateral is a polygon with 4 sides.)
Give students a few minutes to sort and discuss the shapes that are in the three piles: quadrilaterals, triangles, and neither.
As students are working, ask:
- How do you know that shape is a quadrilateral?
- Ask your neighbor to look at where you placed your shape. Do they agree?
Direct students' attention to Question 4. Students are asked to draw a Triangle section and a Quadrilateral section of the zoo. Students can simply draw large rectangular sections on the paper and place each group of shapes in the appropriate section. Tell students to place the shapes in the “Neither” pile to the side for now. They will be addressed later in the lesson.
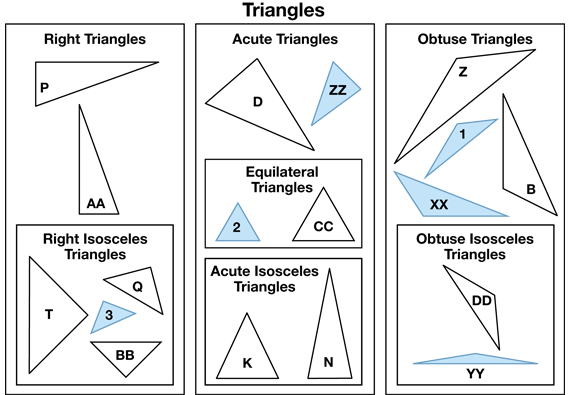
Sort and Classify Triangles. Display all the triangles: Shapes B, D, K, N, P, Q, T, Z, AA, BB, CC, and DD.
- What properties do all these shapes have in common? (Possible response: They all have three sides.)
- What are some properties that the triangles do not have in common? (Possible response: Some have right angles, some have sides that are the same length, and some have small or acute angles.)
Ask students to read Question 5.
- How are you going to figure out which triangles are right triangles? (Possible response: Look for a right angle. Shape AA is a right triangle because one of the angles is 90 degrees.)
- What is an acute triangle? (It is a triangle that has angles all smaller than a right angle or 90 degrees.
Shape K is an acute triangle.)
- What is an obtuse triangle? (It is a triangle with an angle that is larger than 90 degrees.)
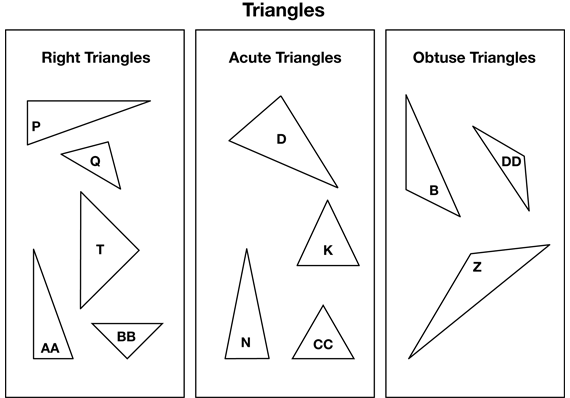
See Figure 1 for a sort of the triangle Shapes Zoo Pieces.
As students are sorting the shapes, circulate, observe, and ask:
- Why did you put [Shape B] with the obtuse triangles?
- What other shapes are [acute]?
- How did you find the right angles? (Possible response: I used the corner of a sheet of paper.)
As students complete sorting of the shapes, ask them to discuss Question 6 with a partner. Display the right triangles: shapes P, Q, T, AA, and BB and discussion Questions 6A–C.
- What is a right isosceles triangle? (Possible response: It is a right triangle with two sides that are the same length or congruent.)
- How can you check if a shape has congruent sides or sides that are the same length? (Possible response: Measure and compare them.)
- What is an equilateral triangle? (It is a triangle with 3 congruent sides.)
- Can a right triangle have 3 sides that are the same length? (no) Why or why not? (All the angles are the same size in an equilateral triangle. They cannot be the same in a right triangle because one angle is 90 degrees. The sum of the other two is 90 degrees.)
Once students have sorted the right triangles, ask them to complete Question 6D. See Figure 2. Students should not attach the triangles to the paper yet. That will be done after all the shapes have been sorted and classified.
Ask students to discuss Questions 7–8 with a partner. See Figure 2 for possible responses and organization of the zoo.
As students work, circulate and ask:
- How did you check if the sides are equal?
- Let me see the shape you drew for [Question 8E]. What section of the zoo does this shape belong in?
- Look at your neighbor's zoo. Are the shapes in your zoo organized the same way?
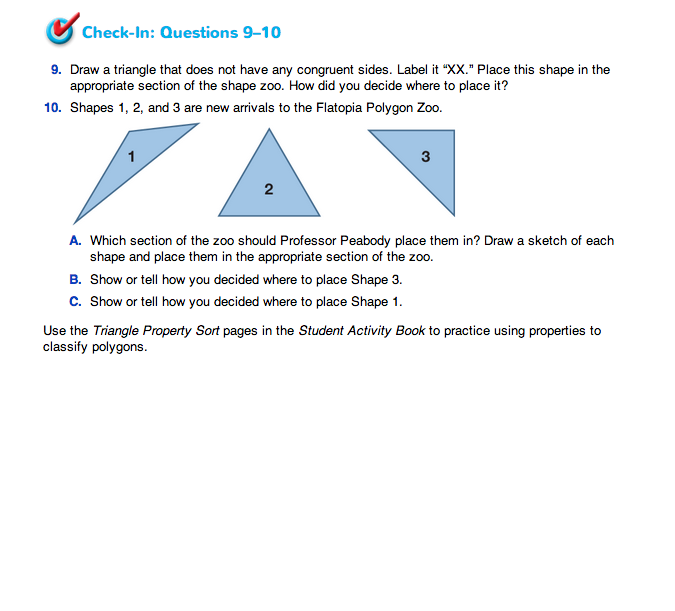
Ask students to complete Questions 9–10 independently.
Students should attach the triangles with tape or a glue stick so their work can be stored to continue work another day.
Use Check-In: Questions 9–10 in the Student Guide to assess students' abilities to identify and describe twodimensional shapes [E4]; classify two-dimensional shapes in a hierarchy based on properties [E5]; and justify conclusions using geometric properties [E7].
Assign the Triangle Property Sort pages in the Student Activity Book for homework.
Scalene Triangles. Scalene triangles are triangles where each side is a different length. They are unusual in that they are defined by what they are not. A scalene triangle has no congruent sides nor equal angles. These triangles are neither isosceles nor equilateral. This label could be added to the zoo but does not need to be.
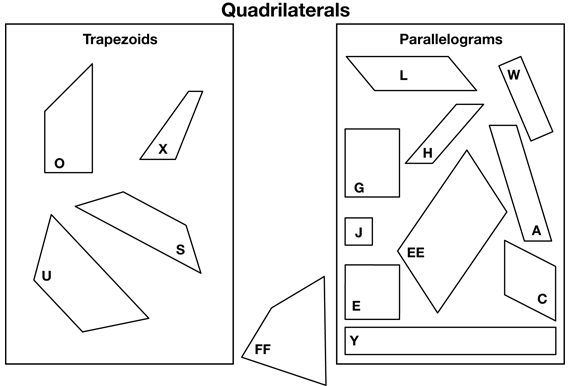
Sort and Classify Quadrilaterals. The zoologist tells Professor Peabody to separate the quadrilaterals into groups. Ask students to discuss Question 11 with a partner. Then have a few groups share their sorting strategy.
- What attributes did you use to sort the quadrilaterals? (Possible response: number of right angles, number of parallel sides, parallelograms and trapezoids)
List these attributes on the board. Then ask students to discuss Questions 12–13 with a partner. As you circulate, try to identify definitions of a trapezoid and parallelogram that can further the discussion of the attributes of these shapes.
- What is a [trapezoid]?
- Does this shape match your definition?
- Does this shape not match your definition?
- Is Shape 6 in Question 12A a trapezoid? (no) Why or why not? (None of the sides are parallel.)
- Is Shape 4 in Question 12A a trapezoid? (yes) Why or why not? (One set of sides is parallel.)
- Is Shape 9 in Question 13A a parallelogram? (yes) Why or why not? (The shape has parallel sides.)
- Is Shape 11 in Question 13A a parallelogram? (no) Why or why not? (The shape has 6 sides so it is not a quadrilateral.)
Have a few different pairs share the definitions for parallelograms and trapezoids. Choose a few shapes to challenge or support each definition. Once students have agreed upon a definition for each type of shape, ask them to complete Question 14 with a partner. See Figure 3. Ask a student to share how they sorted the shapes into trapezoids, parallelograms, and neither.
- Why do you think that shape is a trapezoid? (Possible response: It has four sides and one set is parallel.)
- Why do you think that shape is a parallelogram? (Possible response: It has four sides and both sets of sides are parallel.)
- Is a rectangle a parallelogram? (Yes, because it is a shape with two pairs of parallel sides.)
- Is a square a parallelogram? (Yes, because it is a shape with two pairs of parallel sides. A square also has four sides that are congruent or the same length.)
- Can a parallelogram be a trapezoid? (No, a trapezoid has only one set of parallel sides and a parallelogram has two sets of parallel sides.)
- Do you think this is a good way to sort the quadrilaterals?

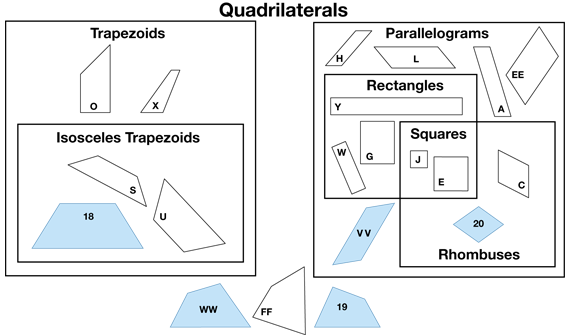
Trapezoid. A trapezoid is a polygon with only one set of parallel sides. Some mathematicians use a different definition of a trapezoid: at least one set of parallel sides. Using this definition, a parallelogram is also a trapezoid. In Math Trailblazers, the more broadly accepted definition of a trapezoid is used: only one set of parallel sides.
Parallelogram. A parallelogram is a quadrilateral with two pairs of parallel sides.
Ask students to complete Question 15 and then discuss Questions 16–17 with a partner.
- What attribute did you decide to use to sort the trapezoids? (Possible responses: isosceles trapezoids; I did not sort them into smaller groups.)
- What attribute did you decide to use to sort the parallelograms? (Possible response: rectangles and non-rectangles; squares and rectangles and parallelograms)
Review student responses to Questions 17B–D.
- What do parallelograms and rectangles have in common? (Possible responses: Both are quadrilaterals that have opposite sides parallel. Rectangles have right angles; parallelograms do not have to have right angles.)
- Why is a square always a rectangle? (A square is always a rectangle because a square will always have 4 right angles like a rectangle.)
- Is a rectangle always a square? (No, a rectangle won't always be a square unless all of its sides are equal.)
- Could Professor Peabody put the square in one of the other piles? (Yes, he could have put the square in the parallelogram pile because a square has opposite sides parallel just like a parallelogram.)
- Are all squares parallelograms? (Yes, because they have opposite sides parallel.)
- Why is a square included as a rhombus? (Possible response: A square has all 4 sides equal. It is a special rhombus because it has all 4 sides equal and has 4 right angles.)
- How can you sort the shapes then?
Read Question 18. The zoologist designs a section of the zoo to accommodate the overlap in the attributes between the parallelograms. Students will draw a similar section on their zoo and place the shapes in the appropriate sections. See Figure 4.
As students complete the sort of the shapes, ask them to add sketches of the shapes shown or described in Questions 19–21. Use the display set of the Shapes Zoo Pieces to display a way to organize the zoo. Ask students to share the shapes they drew in Questions 20–21 and place them in the appropriate section of the zoo.
- Why does that shape belong in that section of the zoo?
- What attributes does that shape share with those other shapes?
- Does this shape share any attributes with another shape?
- What does it mean for a shape to be regular? (Possible response: Regular shapes have sides that are all the same length. For example, a square is a regular rectangle.)
Ask students to complete Questions 22–23 and then discuss student responses. Students can attach the quadrilaterals to the zoo so it can be stored to continue work if needed.
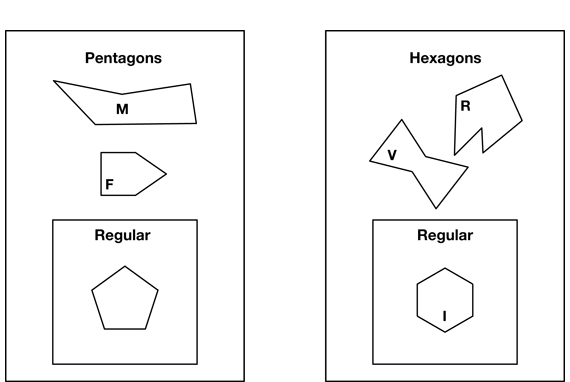
Regular Polygon. A polygon is a regular polygon if it is a two-dimensional shape with closed lines, the shape's sides are all the same length, and all the angles are equal. A regular triangle is an equilateral triangle, and a regular quadrilateral is a square. If all angles of the polygon are equal and all sides are equal, then it is a regular polygon, otherwise it is an irregular polygon.
Sort and Classify Shapes with Many Sides. Display Shapes F, I, M, R, and V, and ask students to take out these shapes from their sets as well.
- What attribute can you use to sort the shapes? (Possible response: Number of sides seems the most obvious.)
Ask students to add these sections to their zoo by completing Questions 24–25. See Figure 5.
Assign the Parallelogram Classification Challenge pages in the Student Activity Book for students to complete independently.
Use the Parallelogram Classification Challenge pages with the Feedback Box in the Student Activity Book to assess students' abilities to identify and describe two-dimensional shapes [E4]; classify two-dimensional shapes based on properties [E5]; justify conclusions using geometric properties [E7]; and show thinking [MPE5].
Assign the Homework section in the Student Guide.