Reading a Map of Alabama. Direct students' attention to the Reading a Map pages in the Student Guide. Display the map on the first page. These pages highlight the use of ordered pairs in the context of a map. Highway maps often number or letter the spaces, not the lines. Scientists and mathematicians number the lines because it is a more precise way of specifying locations. Remind students that locating a city on a map is similar to finding a coordinate on a grid.
To set the stage for the activity, read the story of Suzanne and her family trying to find the town of Fisk, Alabama on a map.
- What do you notice about the grid of Alabama that is similar to the coordinate graphs you have been studying? (Possible responses: it has an origin at (0, 0); it has an x-axis and a y-axis just like the graphs we have been studying.)
To better orient students to the use of the coordinates on this map of north central Alabama, ask students to complete Questions 1–3.
- Where is Athens? (2, 4)
- Where is Union Grove? (6, 1)
- Estimate the distance between Athens and Union Grove. (Possible response: I measured the distance between the two cities to be about 8 cm. 8 cm × 10 miles = 80 miles.)
- Is that the route you would take if you drove from Athens to Union Grove? (no)
- Who would like to show the route they would use to drive from Athens to Union Grove?
Ask a student to use the display of the map to trace the route.
- Did you travel in a straight line? (No, the path was not straight.)
- In the previous lesson you estimated the distance between locations using a ruler and map. How is this different? (Possible response: In the previous lesson the path was straight. Here the path follows the roads or streets.)
- Do you think you can still use the scale to estimate the distance? (Possible response: Yes, I just need to measure the driving path and multiply by the scale.)
Emphasize that sometimes you want to know how far it is from one location to another traveling on the streets, roads, or paths. Other times you want to measure distance “as the crow flies.” If the distance is measured “as the crow flies,” it is measured as a straight line between the two places.
Sometimes a coordinate falls between two lines. Students can either represent this location with .5 or 1/2 to show it is approximately halfway between two coordinates or choose the closest whole-number intersection.
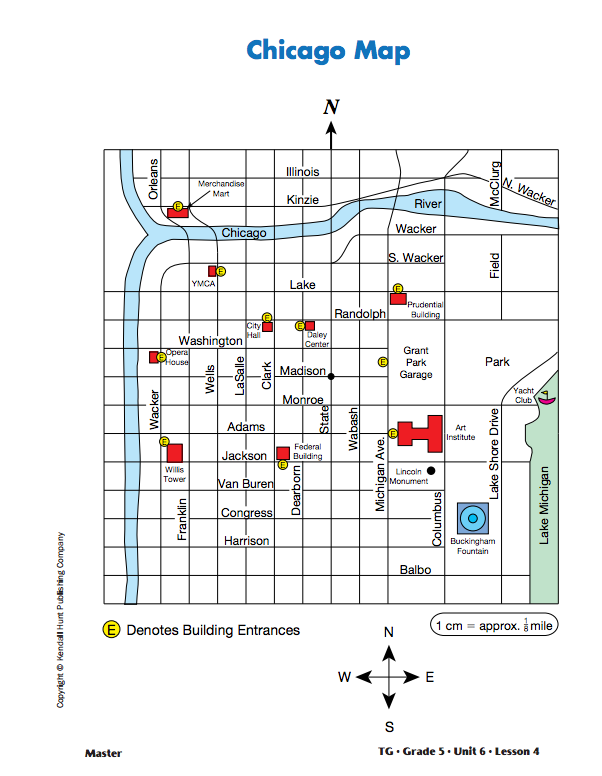
Reading a Chicago Map. Display the Chicago Map Master and give a copy to each student. Explain that the map is set up like a four-quadrant grid. All the addresses in Chicago are given in relation to the corner of State Street and Madison Street, with that corner considered the point of origin (0, 0). Explain that the grid shows the locations of the streets.
The map scale shows that 1 cm = 1/8 mile. Ask:
- What is the point of origin on the Chicago Map? (the corner of State and Madison)
- What ordered pair represents the origin? (0, 0)
- Which street is on the x-axis? (Madison Street)
- Which street is on the y-axis? (State Street)
- Is every grid line shown on the map? (No, some are open areas and do not have grid lines.)
Overlay the Chicago Grid Master over the Chicago Map Master or use the Chicago Map with Grid Master. Ask students to use a ruler to draw the x- and y-axis on the Chicago Map through the intersection of Madison and State.
- What landmark is located at (–1, 2)? (Daley Center)
- Name the coordinates of the Opera House. (–6, 1)
- How far is it from the Opera House to Willis Tower? (about 3 cm, or 3/8 of a mile, straight south on Wacker)
- How did you solve the problem? (Possible response: I used repeated addition. Since it was 3 cm and I knew 1 cm = 1/8 mile, I added 1/8 + 1/8 + 1/8 = 3/8 of a mile.)
- What building is located between (–5, 6) and (–6, 6)? (Merchandise Mart)
- What are the coordinates for the Federal Building? (–2, –)
- What is the location of the Prudential Building? (2, 3)
- How far is the walk between these two buildings if you walk along the streets? (about 10 cm or 11/4 miles)
- How far is the Federal Building from the Prudential Building “as the crow flies”? (about 71/2 cm or a little less than a mile)
- Sam is standing at the corner of Dearborn and Van Buren. He needs to go to the Prudential Building. In what directions and how far does he need to walk? (Possible response: Sam needs to walk 3 blocks east to Michigan Avenue, then 7 blocks north to the Prudential Building for a total of 10 blocks or 11/4 miles.)

Not Quite Chicago. The map is not an exact map of Chicago's downtown area. Not all of the streets are represented. Because city blocks can vary in length, the distances students are asked to calculate should be viewed as approximations.
Solve Distance Problems. Display the sheets of chart paper you prepared. Each chart paper lists two places on the Chicago Map. Organize students into pairs or small groups. Assign two places to each group. The follow-up discussion will be more efficient if two groups are assigned the same set of places.
Tell students to use their map to estimate the distance as if they were walking and “as the crow flies.” Tell students to be prepared to share how they solved each problem. While student groups are working, circulate asking one group of students for each location to record their work on the chart paper you have displayed.