Plot and Sort Triangles. Have students discuss Questions 8–9 in the Student Guide. The questions set the stage for describing properties to sort triangles and quadrilaterals. Emphasize that a property is something about a shape that helps identify it. Some examples of triangle properties would be: size of the angles, right angles or no right angles, or congruent sides. Students will develop these descriptive properties as they sort shapes and describe the properties that guided the sort.
This lesson is an informal inquiry of identification and description of shapes. It sets the stage for a more formal classification hierarchy in Lesson 6. Students using Math Trailblazers have been developing this descriptive language throughout the earlier grades. Students spent a considerable amount of time in Grade 4 describing the properties of polygons and classifying shapes based on their properties.
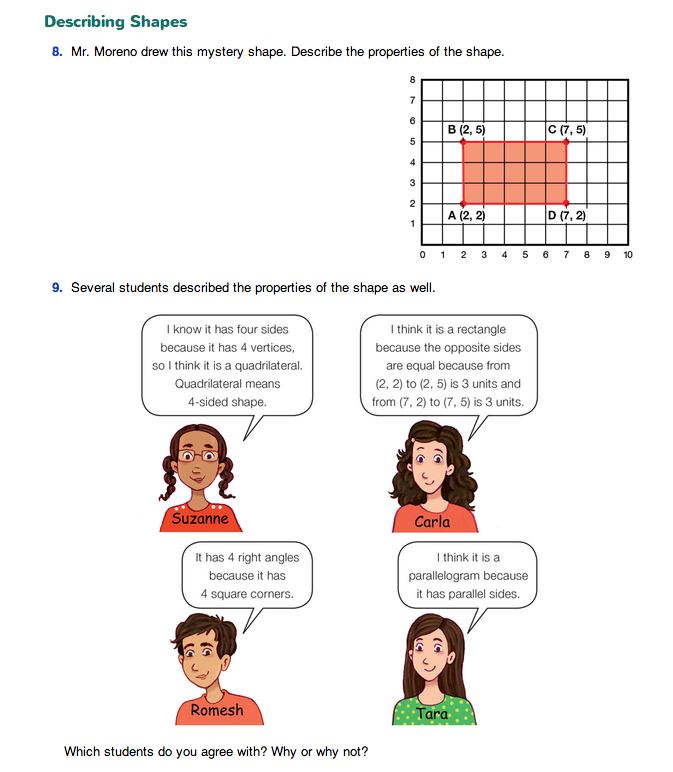
In Question 10 students locate the vertices of triangles described as ordered pairs on the Shape Sort Cards: Triangles pages in the Student Activity Book. Encourage students to use a ruler to connect the vertices. Remind students to label the vertices and color or shade in the shape.
After students have completed all the shapes, ask:
- What did you notice about the coordinates of the shapes?
- Which sets of coordinates made a right angle?
- Which sets of coordinates make obtuse angles?
- Can you name three coordinates that will not make a triangle? (Possible response: As long as the points are different, a triangle can be made.)
As directed in Question 11, ask students to cut the cards apart so the shapes on the eight cards can be sorted into two piles: triangles with right angles and triangles without right angles. Give one pair of students the display set of the cards to sort on the display.
As students are working, circulate and ask:
- How did you decide that a triangle had a right angle? (Possible response: I used the corner of a sheet of paper; the angle looks like the corner of the square grid.)
- Which shapes have right angles? (the shapes on cards 1, 2, and 6)
- Which shapes do not have right angles? (the shapes on cards 3, 4, 5, 7, and 8)
- What sets of coordinates make a right angle? (Possible response: The coordinates (2, 2), (12, 8), (12, 2) make a right angle.)
- Which sets of coordinates make obtuse angles? (Possible response: the coordinates (8, 2), (17, 2), (0, 7))
As students complete the sort, direct them to answer Questions 11 A–E. When most students have completed these questions, discuss student responses.
- What do you notice about the coordinates of the right triangles? (Possible response: the ordered pairs share some of the same numbers. For example: (2, 2), (2, 4), (4, 2) will make a right angle and right triangle.)
- Is the triangle on card 3 a right triangle? (no)
- How do you know? (Possible response: I used a right corner to check.)
- How can the ordered pairs help you decide? (Possible response: The ordered pairs do not share numbers so the sides are not following the grid lines. It is not a right angle.)
Direct students to Questions 12–13. In these questions, students use the cards on the Blank Sort Cards pages to write ordered pairs for triangles.
Ask a few students to share the shapes and the coordinates that they chose.
- How do you know if a triangle is obtuse? (Possible response: This angle is obtuse.)
Now ask students to complete Question 14. Students sort the triangle shapes using a different property.
As students are working circulate and ask:
- What does congruent mean? (the same)
- What if a triangle has three congruent sides? What is this triangle called? (equilateral triangle)
- What if a triangle has two congruent sides? What is this triangle called? (isosceles triangle)
- What if a triangle has no congruent sides? What is this triangle called? (scalene triangle)
Tell students to save these shape cards for activities later in the lesson.
Plot and Sort Quadrilaterals. In Questions 15, students locate the vertices of quadrilaterals described as ordered pairs on the Shape Sort Cards: Quadrilaterals pages in the Student Activity Book.
Before students start plotting the shapes, ask:
- Look at the ordered pairs for each shape. Which shapes do you think have right angles? (Possible response: Shape 10, shape 12, shape 13, shape 15, shape 16, and shape 19 all have right angles.)
- How did you decide? (Possible response: I looked for ordered pairs that shared numbers or each set followed the axis.)
Direct students to plot the shapes and, as directed in Question 16, cut apart the cards and sort them into two piles: shapes with right angles and shapes that do not have right angles. As students complete the sort ask them to answer Questions 16A–C. Focus the discussion on Question 16C.
- What do you notice about the coordinates of the shapes that have right angles? (Possible response: The coordinates have some of the same numbers.)
- Is this set of coordinates for a shape with a right angle: (5, 5), (8, 2), (8, 7)? (Possible response: Yes, the right angle is turned but it is a right angle because a right corner fits.)
Direct students' attention to Question 17. Students use the cards on the Blank Sort Cards pages to write ordered pairs for a different quadrilateral. Ask a few students to share the shapes and the coordinates that they chose. Ask students to place this new shape into the appropriate pile from Question 16.
After this general sort is complete, ask:
- Looking at the group of quadrilaterals with right angles, what do they all have in common? (They all have 4 sides, they all have at least 1 right angle.)
- Look at the shapes that have right angles. What are some ways to sort this group of cards into two piles? (Possible response: all right angles/not all right angles; 4 right angles/2 or less right angles)
Display the shapes on cards 10, 12, and 15.
- Look at these shapes. What are these shapes called? (These shapes are all rectangles. Shape 12 is also called a square.)
- Describe a rectangle. (Possible response: A rectangle is a quadrilateral with four right angles.)
Display the shapes on cards 13, 16, and 19.
- Look at these shapes. What are these shapes called? (These shapes are all trapezoids.)
- Describe a trapezoid. (Possible response: A trapezoid is a quadrilateral with one set of parallel sides. These trapezoids also have two right angles.)
- Do you think all trapezoids have two right angles? (Possible response: I am not sure because I think shape 9 is also a trapezoid but it does not have a right angle.)
Tell students to leave the quadrilaterals with right angles sorted as they answer Question 19. In this question, students sort the shapes that do not have right angles into two groups.
- Look at the shapes that do not have right angles. What are some ways to sort this group of cards into two piles? (Possible response: Both sets of sides are parallel/one set of parallel sides.)
Display the shapes on card 11, 14, 17, and 20.
- Look at these shapes. What are these shapes called? (These shapes are all parallelograms.)
- Describe a parallelogram. (Possible response: A quadrilateral with two sets of parallel sides.)
Add shape card 15 to the cards already displayed.
- Look at these shapes. Is this shape a parallelogram too? (Possible responses: I am not sure because it is a rectangle; yes, because it has two sets of parallel sides.)
- Find all the parallelograms in your quadrilateral cards. (Possible response: Shapes 10, 11, 12, 14, 15, 17, 20 are all parallelograms.)
- Look at the shapes that are not parallelograms. Is there a property they all have in common? (Possible response: They all have 1 set of parallel sides.)
- What are these shapes called? (These shapes are all called trapezoids.)
After discussion, ask students to complete Question 20.
- Look at the shape you plotted in Question 20A. Is this shape a trapezoid? (No, because it does not have a set of parallel sides.) Is this shape a parallelogram? (No, because it does not have a set of parallel sides.)
- What do you think the shape is called? (Possible responses: I do not think it has a special name other than quadrilateral.)
- Look at the shape you plotted in Question 20B. Is this shape a trapezoid? (No, because it does not have a set of parallel sides.) Is this shape a parallelogram? (No, because it does not have a set of parallel sides.)
- What do you think this shapes is called? (Possible response: I do not think it has a special name other than quadrilateral; It looks like a kite.)
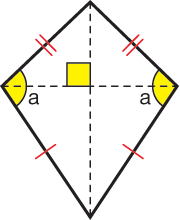
Kite. A kite is a polygon that has two pair of adjacent sides that are congruent. The diagonals of a kite intersect perpendicular to each other and therefore form right angles.