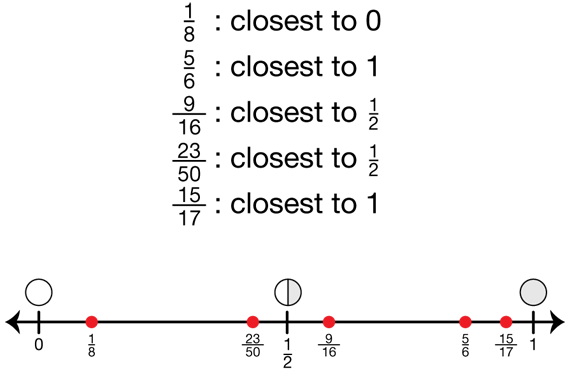
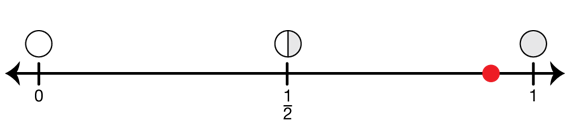
Estimate Fraction Size. Estimation is one of the most effective ways to build understanding with fractions. See Content Note. Students begin the lesson with exercises that strengthen their understanding of the size of fractions. Display the Benchmark Fractions Number Line Master. Ask students to use the number line to help them determine whether the following fractions are closest to 0, 1/2, or 1 and to explain their reasoning. See Figure 1.
1/8, 5/6, 9/16 , 23/50 , 15/17
Estimation and Fraction Number Sense. Devoting time to estimation and fraction number sense is key to developing students who are able to flexibly and confidently approach fraction problems. Estimation is an important part of learning to add, subtract, multiply, or divide fractions. Estimation helps students focus on the meaning behind the operations and helps them assess the reasonableness of their computations. Spending time developing estimation and number sense gives students access to many ways to solve fraction problems. Often a standard algorithm is not needed. Be sure to validate and encourage mental math and invented strategies.
Estimate and Find Fraction Differences. Next, students use benchmark fractions and number sense to estimate fraction sums and differences.
- Find two fractions with a sum that is between 0
and 1. (Possible responses: 1/3 + 1/2; 2/8 + 4/8; 1/5 + 2/10)
- Find two fractions with a difference that is between 0 and 1. (Possible responses: 7/12 − 1/2; 4/5 − 2/10; 3/3 − 2/3)
- Find two fractions with a sum that is between 1/2 and 1. (Possible responses: 2/5 + 2/5; 6/7 + 1/20; 1/2 + 1/8)
- Find two fractions with a difference that is between 0 and 1/2. (Possible responses: 1/10 − 1/25; 4/8 − 2/8; 2/10 − 1/10)
Then display this subtraction problem:
2/4 − 1/3
- What do you notice about the denominators of these fractions? (They are different from each other.)
- What does it mean when two fractions have different denominators? (Possible response: It means the unit whole is divided into different-sized pieces for each fraction.)
- When fractions have unlike denominators, how does it affect the way you add or subtract them? (We can't just add or subtract the numerators since each fraction is made from different-sized divisions of the unit whole.)
- Estimate about where each of these fractions is on the number line and explain why you think so. (Possible response: 2/4 is the same as 1/2, and 1/3 is between 1/4 and 1/2, closer to 1/2. )
- Is the difference going to be greater than or less than 1/2? (less than 1/2 )
- Is the difference going to be closer to 0 or to 1/2?
(closer to 0)
- How can you use the number line to estimate the difference? (Possible response: I consider the lengths of 2/4 or 1/2 and 1/3. I think 1/2 minus 1/3, with 1/3 being a little less than 1/2. So I have a difference that is close to 0.) [See Figure 2.]
Ask students to talk with a partner about how to use mental math or a few written notes to subtract the two fractions.
After a couple of minutes, ask:
- What answer did you come up with? (1/6)
- How did you solve the problem? (Answers will vary. See solutions in the Sample Dialog and Figures 3 and 4.)
If students thought about the problem by picturing fraction circle pieces, have them demonstrate their thinking using the display fraction circle pieces. Students may come up with any number of explanations for how they subtracted. See Content Note.

Develop Conceptual Knowledge. Be sure students develop the concepts and number sense needed to understand the procedures before asking them to use formal paper-and-pencil algorithms for adding and subtracting fractions. It is important to spend ample time developing students' conceptual understanding of fraction operations before moving on to reliance on algorithms. Algorithms do not help students understand what the operations actually mean. When students follow steps they don't understand, the steps are quickly forgotten.
The activities in this lesson will strengthen and extend students' conceptual knowledge so that they can use the procedures with understanding and retain them longer.
Our research and the research of others suggest that students who develop paper-and-pencil procedures before they develop the necessary conceptual understanding and number sense about fractions often calculate without thinking and then cannot look back to see if their answers are reasonable or solve problems flexibly.

Use the Sample Dialog to guide a discussion about mental math strategies.
Teacher: Who wants to explain how they solved 2/4 − 1/3 using mental math?
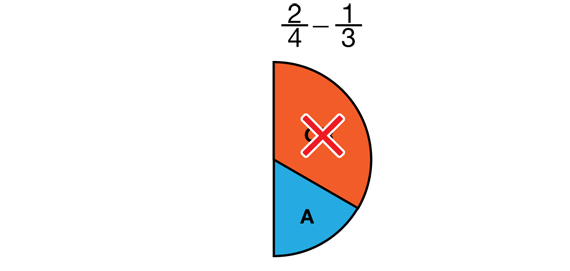
Jackie: We knew 2/4 is the same as 1/2. Then we pictured circle pieces. One pink minus one orange leaves one aqua. That's 1/6 . [See Figure 3.]
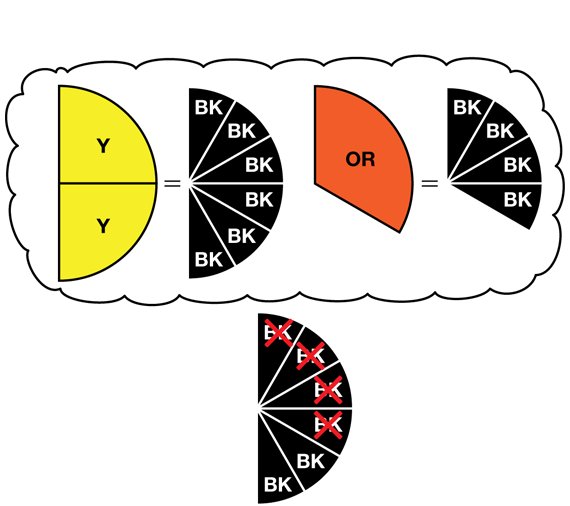
Romesh: We thought about circle pieces. We remembered that the black piece is the only piece that covers both the yellow piece and the orange piece evenly. 2 yellows cover 6 blacks. 1 orange covers 4 blacks. So 6 blacks minus 4 blacks is 2 blacks. That's 2/12 , but we simplified it to 1/6 . [See Figure 4.]
Teacher: Those are two good ways of thinking about the problem. Did anyone think about it another way using a few written notes?
Jessie: We found a common denominator. First we thought of some fractions that are the same as 2/4, like 1/2, 3/6, 4/8, and 6/12. Then we wrote down some fractions that are the same as 1/3 , like 2/6, 3/9, and 4/12 . We picked fractions that had the same denominator and subtracted them. So 3/6 − 2/6 = 1/6.
After students have shared their solutions, ask:
- How did estimating the difference on the number line first help you determine whether or not your answer was reasonable? (Possible response: I
knew that the answer had to be less than 1/2 and closer to 0, so I compared my calculation to where I estimated the answer would be on the number line to see if it was reasonable.)
Estimate and Find Fraction Sums. Display the following addition problem:
1/4 + 2/3
Ask questions to help students estimate the sum:
- Estimate about where each of these fractions is on the number line and explain why you think so. (See Figure 5. Possible response: 1/4 is right in the middle of 0 and 1/2, and 2/3 is between 1/2 and 1, closer to 1/2.)
- How can you use the number line to estimate about where the sum would lie? (Possible response: I look at how long the length from 0 to 1/4 is. Then I find 2/3 on the number line and add the 1/4 length on to it. I estimate that the sum is between 1/2 and 1.)
- Is the sum going to be closer to 1/2 or 1? (closer to 1)
Have students solve the problem with a partner and then ask volunteers to explain the way they solved it. Students should express a variety of ways to solve the problem such as using a fraction circle piece model, mental math, or an invented strategy. These strategies will add to their development and understanding of standard algorithms. Ask volunteers to explain whether or not their solution seems reasonable compared to the estimate they made on the benchmark fraction number line.