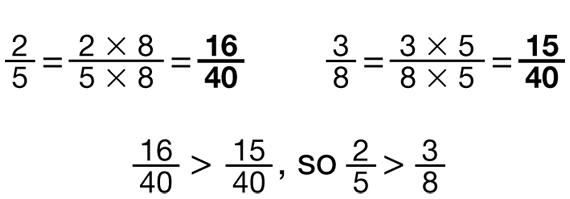Ask students to read the short vignette that precedes Question 9 about Jackie and Jerome putting fractions in order. In this section, students find common denominators to order fractions that are not easy to compare. The problem in the vignette involves putting the fractions 2/5, 1/3, and 1/4 in order from smallest to largest. See Content Note.

Comparing Fractions. When comparing fractions, encourage students to first use mental math strategies before moving to an algorithm for finding common denominators. They can use benchmarks of 0, 1/2, and 1, strategies for comparing fractions with common numerators, and visualizations of fraction circle pieces or the Fractions on Number Lines Chart in the Student Guide Reference section. Students should continue to use and develop their number sense about fractions even as they learn more formal algorithms for computation with and comparison of fractions.
For example, when comparing 1/3 and 1/4, students can reason about which pieces of the whole are smaller when dividing a circle into more pieces. Because the fractional pieces of 1/4 are smaller than they are for 1/3, 1/4 is the smaller fraction. When comparing 2/5 to 1/3, however, students may want to find a common denominator because both the numerators and denominators are different. Alternatively, by using mental math or imagining circle pieces, they may recall that 1/3 can be thought of as 2/6 and then easily compare 2/6 and 2/5. Since the numerators are now the same, “smaller pieces” reasoning shows that 2/6 is smaller than 2/5.

Using Simplest Form. Representing a faction in simplest form may help a student make sense of a fraction, but the simplest form may not help interpret the fraction in a given situation. For example:
There is 3/4 of a cake left. John and Julie each ate 1/8 of the cake. How much of the cake is now left?
3/4 − 2/8 = 6/8 − 2/8 = 4/8 or 1/2
Lily, Lorelei, Ian, and Sean each want a piece of cake, too. Can they each have the same size piece of cake as Julie?
In this example, students can easily see that 4/8 can be shared by four people and that each person can have 1/8 of the cake. This representation more easily represents the situation even though the fraction is not in simplest form. It depends on the context. Students are sometimes asked to respond with the simplest form and sometimes they are not.
Students continue working with partners to order fractions in Questions 9 and 10. Questions 11 and 12 are word problems that involve ordering fractions.
Upon completion, ask students to explain how they compared the fractions presented in Questions 11 and 12. Try to have a variety of methods presented. To compare 4/6 to 3/4 in Question 11, students may refer to the the Fractions on Number Lines Chart and the Fraction Chart from the Student Guide Reference section, use fraction circle pieces, or find and use common denominators. Be sure to ask a student volunteer to demonstrate using the common denominator 40 to compare 2/5 and 3/8 in Question 12. See Figure 2.