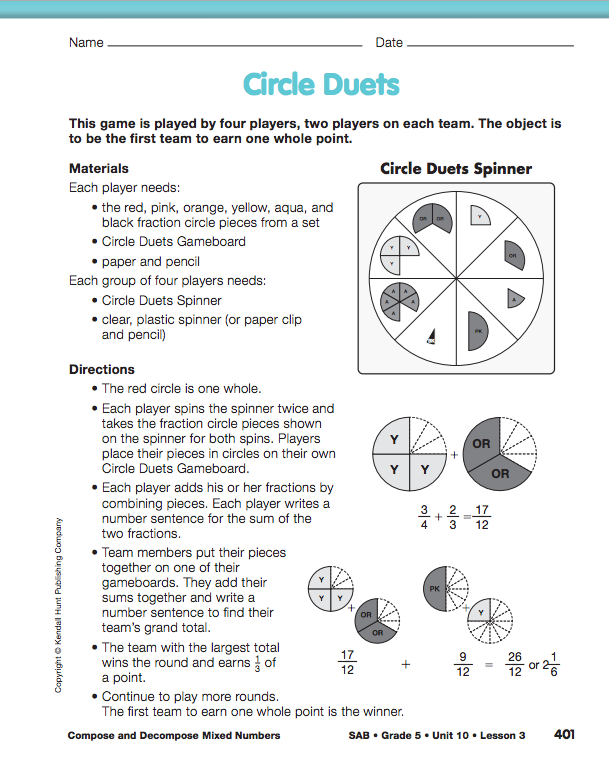
Introduce Circle Duets Game. For this lesson, the red circle is the whole. To play the Circle Duets game, organize students into groups of four—two teams with two players on each team. Use a display of the Circle Duets pages in the Student Activity Book to discuss the directions.
Before play begins, direct students to the Compose and Decompose Mixed Numbers pages in the Student Guide. Discuss Questions 1–3, which highlight two important aspects of the game: representing addition problems using circle pieces and writing number sentences from the resulting sums.
As you discuss Question 1, use the following prompts:
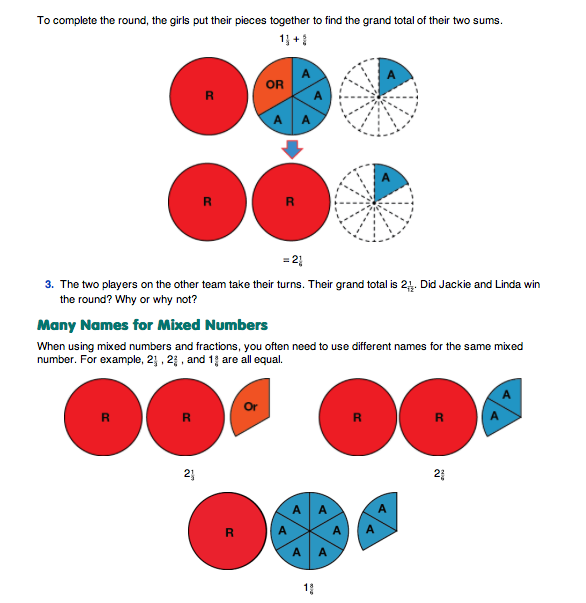
- What fraction circle pieces did Jackie trade?
(Possible response: First she traded the pink [1/2] piece for an aqua [1/6] and an orange [1/3] piece.)
- Why do you think she did that? (She needed a 1/6-piece to complete the first circle. If she took 1/6 away from 1/2, she would have 1/3 left over.)
- How do you know she made a correct trade? (I can put an aqua and orange piece on top of the pink. Together they are the same size as one pink.)
- Did she make another trade? (Yes, after she filled the first circle, she traded six 1/6-pieces for one whole circle piece [red].)
- Could she have made any different trades? (She could have traded the 1/2-piece for three 1/6-pieces.)
- What would have been her answer? (12/6)
- Is that the same as 11/3? (Yes, because 2/6 takes up the same space as 1/3. I can put two 1/6-pieces on top of the 1/3-piece to show they are the same.)
Ask similar questions to those above when you discuss Question 2.
- Is 21/12 more or less than 21/6? How do you know? (21/12 is less than 21/6. Possible response: The black pieces are 1/12 of the circle. They are smaller than the 1/6 [aqua] pieces.)
To clarify the rules, play a sample round of the game with three students using display circle pieces and the display game pages.
Play Circle Duets. As students play the game, they need not find common denominators to find the sums or reduce their answers to simplest form. They can simply use the circle pieces to add and make trades until they can represent the sum as a proper fraction or a mixed number. Instead of concentrating on procedures at this point, encourage students to focus on the reasonableness of the results and modeling the equivalent fractions.
As students add fractions in the game, circulate and ask:
- Should the sums be less than one or more than one? Less than two or more than two?
Discuss Game Strategies. After students have had the opportunity to play Circle Duets, reconvene as a class to discuss some of the strategies students used during the game. Encourage students to share their invented strategies and use their fraction circle pieces to model the following problems. Have a set of display fraction circle pieces and the display of the Circle Duets pages ready if students need them to explain their solutions.
- Linda spun 3/4 and 1/3 and Jackie spun 1/6 and 2/3 playing Circle Duets. Estimate to see if you think their team total will be more than 1 or less than 1.
(Possible response: I think their team total will be a lot more than 1.)
- Will their team total be more than 2 or less than 2? (Possible response: I think their team total will be less than 2.)
- Who would like to explain how they estimated the total? (Possible response: I know 1/3 + 2/3 is one whole. 3/4 + 1/4 would make another whole, but Jackie only spun 1/6, so that would make less than one whole. I think the team total is close to 2.)
- Work with a partner to find each girl's total. One partner should find Linda's total and the other should find Jackie's total. What is each girl's total? (Linda's total is 3/4 + 1/3 = 13/12 . Jackie's total is 1/6 + 2/3 = 5/6.)
- Who would like to show how to add the improper fraction 13/12 to 5/6 to find their exact team total? (Possible response: To find 13/12 + 5/6, I found a fraction equivalent to 5/6 with a denominator of 12, 10/12 . 13/12 + 10/12 = 23/12 , or 111/12 .)
- Is that sum reasonable? How do you know? (Possible response: Yes; I estimated the sum to be close to 2, and 111/12 is very close to 2.)
- Did anyone add the mixed number 11/12 to 5/6? Show us how. (Possible response: I used fraction circle pieces. I know 1 red circle is the same as 12/12 or 12 black pieces, and then I had one more black piece. I knew I had to trade the 5 aqua pieces for 10 black pieces so I would have pieces of all one color. 12 + 1 + 10 black pieces is 23/12 .)
- Did anyone solve 11/12 + 5/6 differently? (Possible response: At first, I only thought about 1/12 + 5/6. I rewrote 5/6 as 10/12 . 1/12 + 10/12 = 11/12 . Then I added 1 + 11/12 = 111/12 .)
Have students save the game materials, or collect the pages to save for Lesson 6. They will have another opportunity to play Circle Duets during the Workshop.