Multiply Fractions by a Whole

Est. Class Sessions: 2

Developing the Lesson

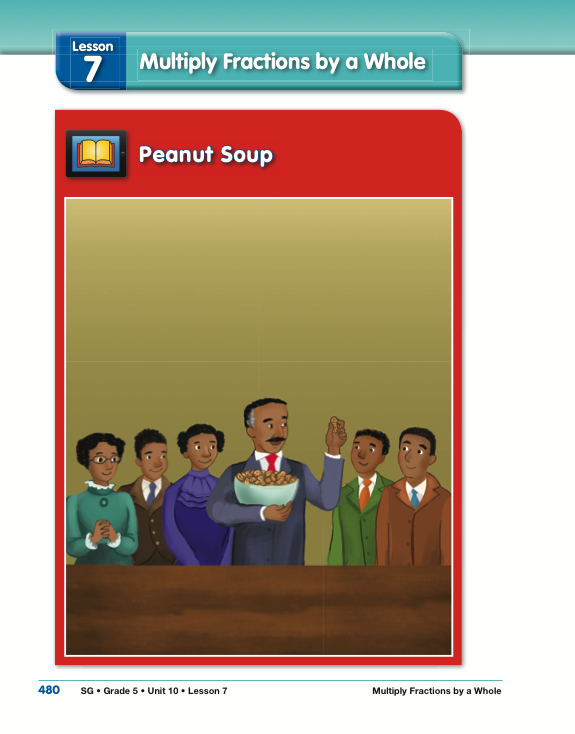
Read Peanut Soup. Students begin the lesson by reading the story “Peanut Soup” in the Multiply Fractions by a Whole pages in the Student Guide. In the story, George Washington Carver shows his students at Tuskegee Institute the many food and nonfood products that he has been able to derive from peanut products in his lab. Carver and his students demonstrate the versatility of peanuts in a dramatic way by inviting a group of skeptical businessmen to a luncheon of dishes that contain peanuts. The meal is a great success, and Carver convinces the businessmen that supporting peanut farmers will be a good investment.

Explain that the story is based on more than one true incident in George Washington Carver's career in Tuskegee. To stage presentations of his work with the peanut, sweet potato, or cowpea, Carver delighted in serving meals made entirely with dishes containing these items. He waited until after the guests had finished their meal to tell them what they had eaten. He took the opportunity to demonstrate other nonfood uses of the legume as well and won over many skeptics in this way.

Have student volunteers read the story aloud. Pause to use the following discussion prompts to lead a class discussion. Be sure to discuss the multiplication problems presented in the story, 1/20 × 70, 4 × 31/2, and 12 × 1/4 . Encourage students to use any strategy or model that makes sense to them such as repeated addition, invented strategies, fraction circle pieces, number lines, or drawings when solving these problems.

Tuskegee Normal and Industrial Institute was founded in 1881 by Booker T. Washington as a school where African-Americans could learn to use science in practical ways. Its students were of diverse ages and economic backgrounds; some lived at the school, and some lived nearby. In addition to their studies, students worked at the school by farming the gardens, tending the animals, helping in the kitchens, or constructing new buildings. The Tuskegee Archives contain records of African American history since 1896. Today Tuskegee Institute and the Carver Foundation continue research in the natural sciences.

Page 482

Ask:

What had Professor Carver been working on so hard in his lab? (He had been developing products made from peanuts.)
What kinds of products did Carver make from peanuts? (shoe polish, face cream, milk, shaving cream, linoleum, house paint)

Page 483

Ask:

What are legumes, and how do they affect the soil?
What was Carver's promise to the farmers? What did he do to try to keep it? (Carver promised the farmers that they could make a profit selling peanuts. He experimented and found many new uses for the peanut.)

Legumes are a family of plants including peas, beans, soybeans, peanuts, and clover. Legumes play a very important role in the process of farming. Nodules on the roots of legumes contain special bacteria capable of transforming unusable atmospheric nitrogen into a form of nitrogen which is usable by living organisms. This process is called nitrogen fixation.

Page 484

Ask:

Why did Carver want the businessmen to know the many uses of the peanut? (so they would buy the farmers' peanut crops and open factories to make peanut products)
What was Louis's idea? (to have a big dinner of their favorite peanut dishes for the businessmen in order to impress them)

Page 486

Ask:

Why did Eugene get too much flour for Alberta? (He followed a recipe exactly without considering the number of people it would serve.)

Page 487

Ask:

What is a ratio? Give an example from the story. (A ratio is a comparison of quantities, often expressed as a fraction. The ratio involved here is the number of people served at the luncheon compared with the number of people served by Alberta's recipe (12 people/240 people).)

Page 488

Ask:

How would you find 1/20 of 70 pounds of flour? (Answers will vary. See Figure 1 for a possible solution.)

Page 489

Ask:

If there are about 4 cups of flour in a pound, how many cups do you need for 31/2 pounds? How would you solve this problem? (14 cups; Solutions will vary. Alberta changed 31/2 pounds to 7/2 pounds and then multiplied 7/2 by 4. Another strategy is to multiply 4 × 1/2 by multiplying 4 × 3 = 12 and 4 × 1/2 = 2. Then 12 + 2 = 14 cups.)
How many tablespoons are in a quarter-cup (one-fourth cup)? (4 tablespoons)
How many times will Josephine have to refill the quarter-cup to measure 12 tablespoons? (3 times; She needs 3/4 cup of flour.)

Page 490

Ask:

Why did Carver want to have greens with the meal? Why did he want several different kinds? (According to the story, a mix of greens tastes better than a single type of green by itself. Also, the greens provide nutritional balance.)

George Washington Carver wrote bulletins about the
medicinal and nutritional properties of wild plants and vegetables. During the first World War, his bulletins helped people locate, harvest, and prepare wild greens that were not only good to eat, but also good for them. One such green was the pokeweed as shown here.

Page 491

Ask:

Were the guests surprised to learn that all the dishes contained peanuts? Was the luncheon a success? (Yes. The businessmen enjoyed all the dishes and were amazed to find that there were peanuts in all the dishes. They agreed that peanuts might be profitable.)

Multiply to Change Recipes. After the story, display and direct students' attention to the Peanut Butter Cookie Recipe Master. Explain that this recipe makes 1 dozen cookies.

Ask:

How can you change this recipe so that it will make 4-dozen cookies? (Multiply each ingredient's amount by 4.)
Work with a partner and change the amount of each ingredient so that the recipe yields 4-dozen cookies.

After students have had some time to use invented strategies, repeated addition, fraction circle pieces, drawings, mental math, number lines, and other strategies to multiply fractions by 4, ask a few to share their strategies.

Next, direct their attention to the Multiply to Change Recipes section of the Multiply Fractions by a Whole pages in the Student Guide. Discuss the vignette at the top of the page. Professor Carver's student, Alberta, converts a recipe that makes 1-dozen cookies to one that makes 4-dozen cookies. Discuss the variety of strategies Alberta uses to multiply fractions by a whole number.

Show students a set of measuring cups and measuring spoons. This helps students not familiar with the vocabulary to visualize what is going on in the problems on the Multiply Fractions by a Whole pages in the Student Guide.
For students having trouble getting started with converting the recipe in Question 2, ask them to first imagine they are simply doubling the recipe. This may help these students better understand the problem.
Some students may get frustrated with multiplying 11/4 × 3 in Question 2. Let students invent strategies and ways of thinking about this problem. Some students may apply the distributive property and break this problem into 1 × 3 + 1/4 × 3 making 11/4 × 3 = 33/4. Others might think of this problem as 11/4 is 5/4, and then 5/4 + 5/4 + 5/4 = 15/4 = 33/4.

Assign Questions 1–2 to student pairs. In Question 1, students should remember that changing the order of the factors in a multiplication problem does not change the result. Fraction circle pieces are used to model 4 × 3/4 as repeated addition, and students use them to show that 3/4 × 4 yields the same product. Students should see that 3/4 of 4 will be less than 4 because they are finding a part of 4.

In Question 2, students use any strategy they like to multiply fractions by a whole and convert a recipe that serves 4 to one that serves 12. Circulate as students work and observe the strategies students choose to solve the problems.

Upon completion, try to select students who can demonstrate a variety of solution strategies and discuss Question 2.

Ask:

How does the recipe need to change in order to serve 12? (The amount of each ingredient needs to be multiplied by 3.)
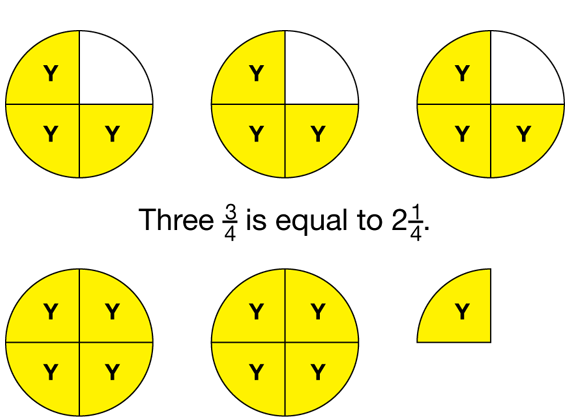
Who can show how to use fraction circle pieces to multiply 3/4 - cup of milk by 3? (3 yellow pieces cover 3/4 of a red circle. 9 yellow pieces pieces cover 2 whole circles and 1/4 of another one. 21/4 cup milk is needed to serve 12. See Figure 2.)
When you multiply 3/4 by 3, is the product greater than or less than 3? Why? (The product is less than 3 because you are only taking a part, 3/4, of 3.)
Who would like to show how to use a number line to multiply 2/3 - cup of salsa by 3? (3 hops of 2/3 is 6/3 or 2. 2 cups of salsa are needed to serve 12. See Figure 3.)
Did anyone use repeated addition or a multiplication strategy? Show us. (Possible response: For the chicken broth, 1/2 + 1/2 + 1/2 = 3/2 or 11/2 cups.)
Show how to use a different strategy to check this answer. (Possible response: For the chicken broth, you can use mental math to check your answer. Think about fraction circle pieces. Add a pink half + a pink half to get 1 red circle, and then add on another pink half to get 11/2.)
How did you determine how much cheese was needed to serve 12? Did anyone break the fraction apart? (Possible response: I broke the fraction into two parts, 1 and 1/4. 3 × 1 = 3 plus 3 × 1/4 = 3/4. 3 + 3/4 = 33/4 cups of cheese.)
Did anyone think of 11/4 as an improper fraction when solving 11/4 × 3? Show us. (Possible response: 11/4 is 5/4. If you have 5 fourths, and you need 3 times that, you would need 3 × 5 fourths, or 15 fourths.)
What is 15/4 in simplest form? (33/4)
Do you think it makes more sense to say 15/4 cups of cheese or 33/4 cups cheese? (Possible response: It may be easier to measure 3 whole cups and 3/4 cup more cheese rather than fifteen 1/4 - cups of cheese.)
Which is easier to understand: 15/4 hours or 33/4 hours? (33/4 hours; Sometimes it makes more sense to talk about things in simplest form.)
Is it reasonable that the product of 11/4 × 3 is greater than 3? Why or why not? (It makes sense because 11/4 is greater than 1. You multiply the 3 by 1 and then by a little more.)

Assign Questions 3–8 to student pairs and then discuss students' answers upon completion. In Question 3, students can use a diagram to help them multiply fractions by whole numbers. They are being asked to find a fraction of a whole, for example, 1/4 of a dozen or 1/4 of 12. This type of diagram or set model makes sense in this situation because students can see and count the number of cookies in each serving. The commutative property states that these numbers can be switched, but it is important that students understand this problem context is different from 12 groups of 1/4. An example of this “find wholes of fractions” context is presented in Question 5 when students multiply 1 × 3/4, 2 × 3/4, 3 × 3/4, etc.

Help students understand the effects of factors less than and greater than 1 on the product of fractions. Multiplying fractions that are greater than 1 (e.g., 524 , 624 ) will result in a product greater than 12 (Question 3G). Multiplying 12 by fractions less than 1 (e.g., 124, 224, 324 ) will result in a product less than 12 (Question 3H).

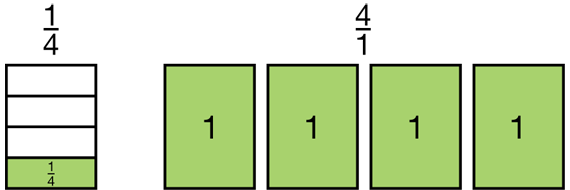
In Question 4, students are asked to explain the difference between the meanings of 1/4 and 4/1. For the fraction 1/4, there are 4 equal parts and we are interested in 1 of the parts. For the fraction 4/1, the 1 in the denominator tells us that all of the items in the whole set are in one group. The 4 in the numerator means that we are interested in 4 whole groups, so 4/1 is equivalent to 4 whole groups. See Figure 4.

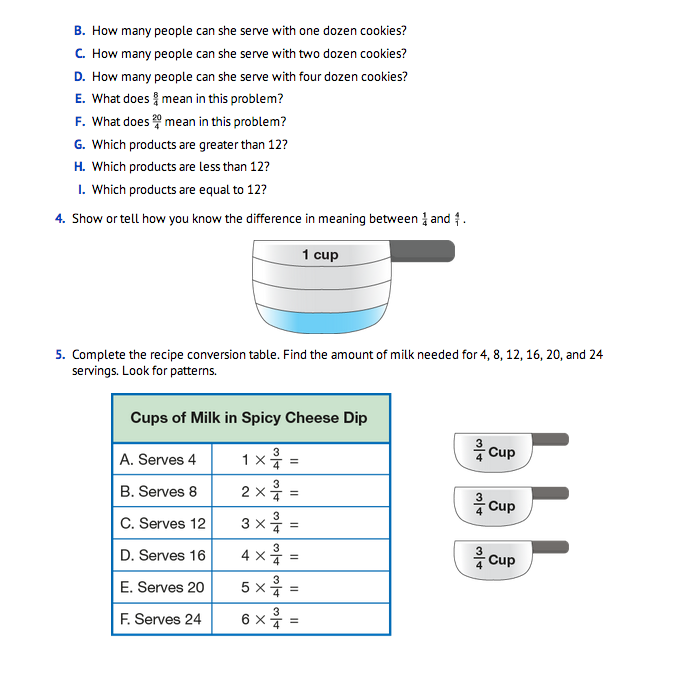
In Question 5, students look for patterns in the multiplication sentences in a table. These problems can be solved by repeated addition; for example, 3/4 × 3 is 3/4 + 3/4 + 3/4 = 9/4. Some students may begin to see that they if they rename each whole number as an improper fraction (e.g., 4 = 4/1), they can multiply the numerators of each fraction together and multiply the denominators of each fraction together to solve the problem. Others may see that they can simply multiply the whole number factor by the numerator.

In Questions 6–8, students are presented with more ways to multiply fractions by whole numbers. A partitioning strategy is presented in Question 6. In Question 7, students begin practicing Luis's paper-and-pencil method for solving 3/4 × 5. He multiplies the numerator 3 times the whole number 5 to find 5 times three-fourths and finds 15/4. Remind students that Luis is multiplying 5 times 3 parts, and the kind of parts is fourths. In Question 8, students are shown a solution using rectangle models.

Solve Party Problems. After discussing students' responses to Questions 3–8, assign Questions 9–16. Students solve word problems involving multiplication of fractions by whole numbers. Encourage students to use any strategy that makes sense to them when solving the problems.