Discuss students' solutions to some of the problems in Questions 4–18. Ask a student to demonstrate how he or she found the area of one of the rectangles in Question 4B or 4C. It is likely that students will use a rectangle model.
- Why did you pick this strategy? (Possible response: I used a rectangle model because I could not do the calculations in my head. It was easier to see what I needed to calculate.)
- Were there some questions you could answer by estimating? Which ones? How did you know?
(Questions 10, 11C, 14B, 16B, 17; there were clues in the question like “about” and “closer to.” Some of the questions did not provide exact amounts or measurements, so I could not find an exact answer.)
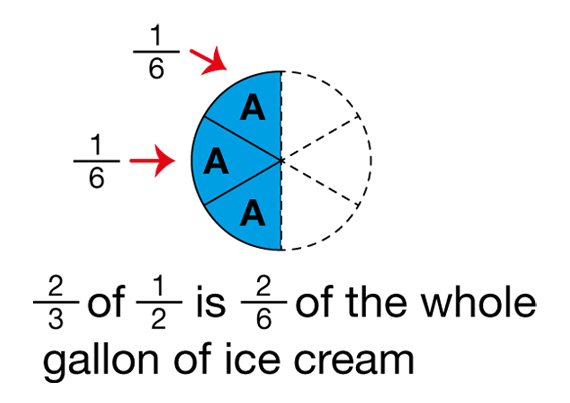
- Show how you solved the problem in Question 11A, 2/3 × 1/2. (Possible response: I used fraction circle pieces. 3 aqua pieces divide a pink half into thirds. 2 aqua pieces show 2/3 of 1/2. Since 6 aquas cover the whole, 2 show 2/6 or 1/3.) [See Figure 3.]
- Did someone use a different strategy to solve the problem in the Question 11B? (Possible response: I reasoned that one-half of a purple tenth would be one-twentieth. I used paper and pencil to check 1/2 × 1/10 = 1/20.)
- Why did you pick this strategy? (Possible response: I could picture the model in my head. It was easier and more efficient to reason and use paper and pencil than to use fraction circle pieces or fold paper.)
- Did the problem in Question 12 require an exact calculation or an estimate? (exact)
- How did you solve it? (Possible response:
I knew 1/4 of 24 is 6, so I multiplied 6 three times to get 3/4 of 24 equals 18.)
- How do you know that a product of 18 makes sense? (Possible response: It makes sense because one-half of 24 is 12, so 3/4 of 24 should be a little more than that.)
- Did anyone solve 3/4 × 24 a different way? (Possible response: Since I knew the whole was 24 and that I could divide 24 into fourths, I sketched a diagram.)
[See Figure 4.]
- How do the multiplication problems differ in Question 11 and Question 12? (In Question 11, I had to multiply two fractions together and in Question 12, I had to multiply a fraction by a whole number.)
- Do your multiplication strategies change based on the problem? Is there a strategy that you prefer?
It is likely that students will be moving toward a paper-and-pencil procedure at this point. Some may still feel more comfortable modeling the problem. While fraction circle pieces are limited, rectangle models are very versatile representations. Students can move from paper folding to simply sketching and dividing a rectangle.
Direct students' attention to Check-In: Questions 19–21. Before students begin working, display and direct their attention to the Math Practices page in the Student Guide Reference section.
To focus their attention on MPE1, 2, 3, 5, and 6 ask:
- What does it mean to “know the problem” [MPE1]? (Possible response: It means you have read the problem carefully so you know what you need to figure out and what questions to answer. You need to know what information in the problem is important and what kind of operation to perform to get the answer.)
- What kinds of strategies can you use to solve fraction multiplication problems [MPE2]? (Possible responses: draw pictures, fold paper, sketch rectangles, use fraction circle pieces)
- How can estimation help you check for reasonableness [MPE3]? (Possible response: I can estimate the product and compare my answer to my estimate. If my answer doesn't make sense, I can try again.)
- How can you clearly show your work [MPE5]?
(Possible response: I can clearly show the steps I took to solve the problem. I can draw a picture and include number sentences.)
- Why is important to use labels [MPE6]? (Possible response: It's important to include labels in our work and answers to show what the numbers mean.)
Assign Check-In: Questions 19–21 for students to complete individually.
Use Check-In: Questions 19–21 on the Solving Fraction Multiplication Problems pages in the Student Guide with the corresponding
Feedback Box in the Teacher Guide to assess students' abilities to solve word problems involving multiplication of fractions [E5]; represent multiplication of fractions with number sentences, drawings, and stories [E3]; multiply fractions [E4]; explain the effects of factors less than and greater than 1 on the product of fractions [E6]; choose appropriately from among estimation and computation strategies [E7]; know the problem [MPE1]; find a strategy [MPE2]; check for reasonableness [MPE3]; show work [MPE5]; and use labels [MPE6].
Use the Workshop in Lesson 11 to provide targeted practice.