Assign Check-In: Questions 10–15 to provide practice renaming mixed numbers and improper fractions. Some can be modeled with fraction circle pieces and others cannot. After students have had a chance to show the fraction in simplest form, discuss Question 11. Ask students to find other ways to show 117/8 using the circle pieces or a circle model.
See Figure 5.
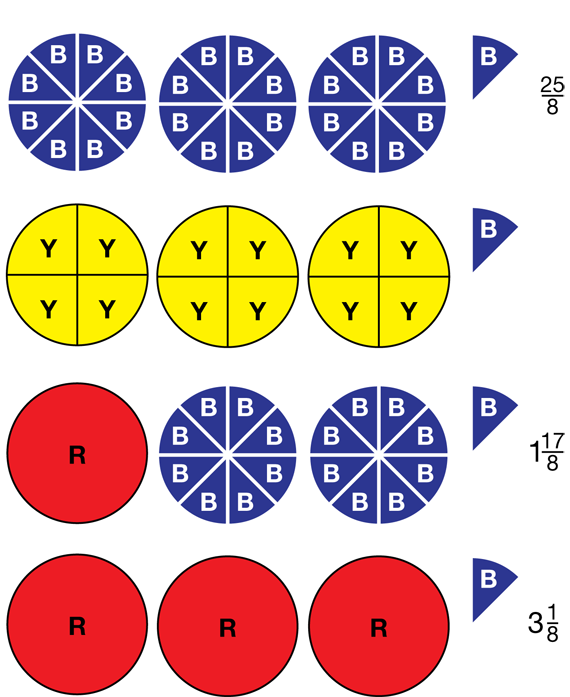
- How do you know these are all equal to 117/8? (They all cover the same amount of space.)
- How do you know which of these representations is in lowest terms? (31/8 uses 2 colors and the fewest pieces.)
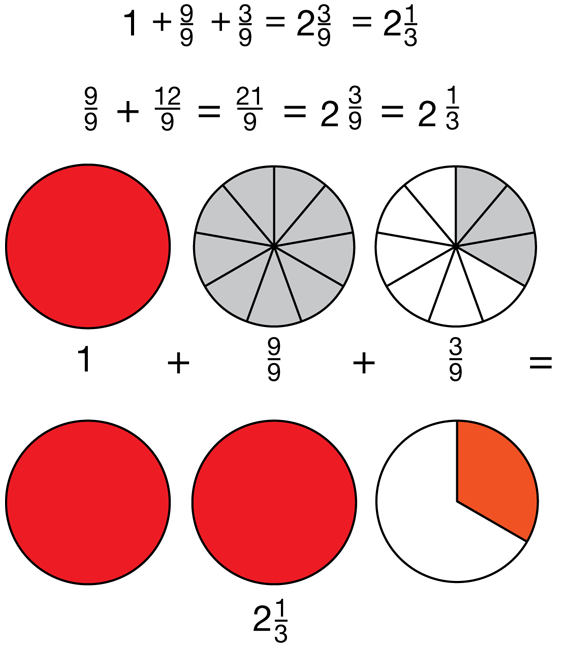
Discuss students' strategies for Question 13, which is a problem that cannot be represented by the fraction circle pieces. Students should have a variety of strategies for this problem. See Figure 6 for ways students might represent 112/9 by drawing a circle model.
Explain to students that it is helpful to be able to rename mixed numbers so that you can add them easily. This will help them learn to use paper-and-pencil methods to add mixed numbers.
- Imagine a Circle Duets game with fractions like 5/7 and 8/9 on the spinner. Can you model these fractions with fraction circle pieces? (no)
- Can you make a ninth by putting an aqua [sixth] piece together with an orange [third] piece? Does this make sense? (No, because ninths are even smaller than sixths or thirds.)
- Can you make a seventh by putting a yellow [fourth] piece together with an orange [third] piece? Explain why you think so. (Possible response: No, because a piece of a circle cut into 7 equal shares would be smaller than a piece of a circle cut into either 4 or 3 equal shares.)
- Imagine you wanted to find a team total and had to add 15/7 + 8/9. Can you think of a strategy to help you rename these mixed numbers without using circle pieces? (Possible response: When I added fractions with unlike denominators, I found common denominators by multiplying the denominators together. 63 is the common denominator. 145/63 + 156/63 = 2101/63 or 3 38/63.)
In the next lesson, students will continue to practice renaming mixed numbers with fraction circle pieces and other strategies as they learn to use paper-and-pencil methods to add mixed numbers.
Use Questions 10–15 on the Compose and Decompose Mixed Numbers pages in the Student Guide to assess students' abilities to find equivalent fractions for mixed numbers [E1]; represent and identify the simplest form of a fraction [E2]; name and represent fractions greater than one as mixed numbers and improper fractions [E3]; add mixed numbers using fraction circle pieces [E8]; show work [MPE5]; and find a strategy [MPE2].
The Workshop in Lesson 6 provides targeted practice.