Use a Variety of Strategies. Ask students to read the problem about Jackie and Jerome's mosaic in the Using Common Denominators pages in the Student Guide.
- Where have you seen mosaic patterns? (Answers will vary. Possible response: artwork in museums, public murals, tile patterns on floors, walls, or ceilings)
- What shapes do you often see in mosaic patterns? (Possible response: squares, rectangles, triangles, polygons, circles)
Assign Questions 1–8 to student pairs. Students begin by estimating the fraction sum in Jackie and Jerome's problem. They show their estimates on a number line (Question 1).
As students discuss their estimates with their partners, probe students' thinking using prompts similar to those in the Sample Dialog and the following:
- Where is 3/4 on the number line? (halfway between 1/2 and 1)
- Where is 1/6 on the number line? (a third of the way between 0 and 1/2)
- Where do you think 3/4 + 1/6 would be on the number line? (close to 1)
- Do you think the sum will be greater than 1/2? Why?
(Yes, because 3/4 is more than 1/2.)
- Will the sum be closer to 1/2 or to 1? (1)
- Will the sum be closer to 3/4 or to 1? (1)

Use this dialog to discuss Question 1 in the Student Guide.
Teacher: Where do you think 3/4 + 1/6 would be on the number line?
Grace: I think it would be between the 1/2 and the 1.
Teacher: Why do you think so?
Grace: Because the first number is 3/4. That is halfway between the 1/2 and the 1. Then 1/6 is just a little more.
Teacher: What do you think, Nicholas?
Nicholas: I think that's right.
Teacher: Do you think it should be very close to where 3/4 is, or closer to 1?
Nicholas: I think right by 3/4, maybe just a little further.
Teacher: Further in which direction?
Nicholas: This way. [points to the right]
Teacher: Why do you think it should be there?
Nicholas: Because it's like Grace said. You already have 3/4, and then 1/6 is just a little more to the right.
Teacher: What if you thought about circle pieces?
Grace: Oh. I guess it would be closer to 1 and not as close to 3/4.
Teacher: Do you agree, Nicholas?
Nicholas: Yeah, I think so. [grabs an aqua piece] This is pretty big. It makes it closer to 1. So the answer should be about here. [points to location a little to the right of halfway between 3/4 and 1]
Students find an exact answer to the problem in Question 2. Encourage them to use any method they find efficient to arrive at an exact answer. They may calculate by finding a common denominator numerically, by using the one-color method with fraction circle pieces, or by using a variation on either of these methods as they were developed in Lesson 1.
Have students work in pairs to read Jerome, Jackie, and Ana's methods for finding an exact answer for the fraction sum. Jerome uses a numerical method to find a lowest common denominator and to add the fractions. Jackie uses the one-color method with fraction circle pieces. Ana uses a multiplication facts chart to help her find equivalent fractions.
In Question 3, students compare Jackie's and Jerome's methods and make connections between them. Questions 3C and 3D ask students to use fraction circle pieces to explain parts of Jerome's procedure for finding a common denominator. These explanations may be challenging for students, but it is important that they be able to make connections between the model and the computational procedure. In Questions 4 and 5, students explore the common denominator method and its connection to the one color method for a subtraction problem. Questions 6–8 provide more practice with these skills and concepts. See Content Note.

Question 6E and 6F involve addition and subtraction problems with three terms. For these types of problems, encourage students to look for flexible and efficient strategies. With three denominators, it can be difficult for students to find one common denominator since they must find a common multiple of three numbers instead of two. It may be inefficient to multiply all three denominators together if that is the method they are used to. Encourage them to look for lower common denominators to keep the arithmetic simpler, if possible. In Question 6E, for example, multiplying all three denominators together would result in a common denominator of 200, making the rest of the computation complicated. Encourage students to check multiples of the largest denominator to see which is also a multiple of the other two. By this method, students will quickly discover the lowest common denominator of the three fractions to be 20.
Other efficient methods include adding or subtracting two of the fractions that are easy to calculate first, then combining the first result to the third term. This often avoids large common denominators. For example, for Question 6E, students will likely be able to identify 10 as a common denominator for 5ths and 10ths: 1/5 + 3/10 = 2/10 + 3/10 = 5/10. Since 5/10 simplified is 1/2, they can then easily add 1/2 to 1/4 to get 3/4.
Discuss Strategies and Models. Upon completion of Questions 1–8, discuss the connections between the conceptual model (circle pieces) and the computational procedure (finding a common denominator) that students are learning. Have a display set of fraction circle pieces ready and display the addition problem discussed in Question 3:
3/4 + 1/6
- Show how Jerome found the lowest common multiple of 4 and 6. (Possible response: He wrote some of the multiples of 4: 4, 8, 12, 16, 20, and 24. Then he wrote some of the multiples of 6, 6 and 12, until he found a common multiple. 12 is the lowest common multiple of 4 and 6.)
- What did Jerome do with the 12? (He used the 12 as the common denominator for fractions equivalent to 3/4 and 1/6.)
- Show how Jerome rewrote the fractions 3/4 and 1/6 using the common denominator, 12. (Jerome multiplied both the numerator and denominator in 3/4 by 3 and got 9/12 . Then he multiplied both the numerator and denominator in 1/6 by 2 and got 2/12 .)
- Is 9/12 equivalent to 3/4? Show us with fraction circle pieces. (Yes; 9 black pieces cover the same amount as 3 yellow pieces. It is the same area,
just cut up into different parts. Instead of 4 parts, it is 12 parts total.)
- What single color of the fraction circle pieces did Jackie use to cover both 3/4 and 1/6 exactly? (black)
- How many black pieces cover the red circle? (12)
- How many black pieces are needed to cover each yellow piece? (3 black pieces are needed to cover each yellow piece.)
- How many black pieces are needed to cover 3 yellow pieces? (9 black pieces cover 3 yellow pieces.)
- Think about Jerome multiplying both the numerator and denominator of 3/4 by 3. Instead of 4 parts, he has 12 parts total. Why did Jerome multiply the numerator and denominator of 3/4 by 3? (Possible response: He has 12 parts now instead of 4. A black piece is a twelfth of the red circle and a yellow piece is a fourth of the red circle. Since there are 3 twelfths in every fourth, he multiplied 3 × 3 = 9 and 4 × 3 = 12 to get 9/12 .)
- Is 2/12 equivalent to 1/6? Show us with fraction circle pieces. (Yes; 2 black pieces cover the same amount as 1 aqua piece.)
- Think about Jerome multiplying both the numerator and denominator of 1/6 by 2. Instead of 6 parts, he has 12 parts total. How many black pieces are needed to cover every aqua piece? (2 black pieces are needed to cover every aqua piece.)
- Why did Jerome multiply the numerator and denominator of 1/6 by 2? (Possible response: He has 12 parts now instead of 6. A black piece is a twelfth of the red circle and an aqua piece is a sixth of the red circle. Since there are 2 twelfths in every sixth, he multiplied 1 × 2 = 2 and 6 × 2 = 12 to get 2/12 .)
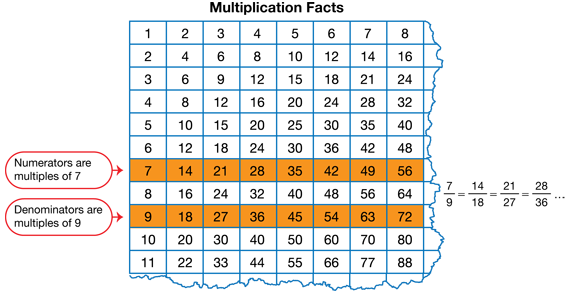
Distribute and display the chart on the Multiplication Facts Master. Students can write on these copies as needed. Students can also look at the identical Multiplication and Division Facts page in the Student Guide Reference section. Discuss Ana's strategy for finding equivalent fractions. Remind students that this is similar to one of the methods they used in Lesson 1 when they listed equivalent fractions until they found ones with common denominators.
- Who would like to show how Ana used a multiplication facts chart to find equivalent fractions? Explain how she found fractions equivalent to 3/4. (Possible response: Ana found the row with the multiples of 3 because 3 is the numerator, and the row with the multiples of 4 because 4 is the denominator. The equivalent fractions are 3/4, 6/8, 9/12 , 12/16 , and so on.)
- Explain how Ana used the multiplication facts chart to find fractions equivalent to 1/6. (Possible response: Ana found the row with the multiples of 1 because 1 is the numerator, and the row with the multiples of 6 because 6 is the denominator. The equivalent fractions are 1/6, 2/12 , 3/18 , 4/24 , and so on.)
- How did she choose fractions with a common denominator? (Ana saw that both 9/12 and 2/12 have a common denominator of 12.)
- The Fractions on Number Lines Chart can help you find equivalent fractions, but ninths are not listed on that chart. Who would like to explain how to use a multiplication chart to find fractions equivalent to 7/9? (See Figure 1. Find the multiples of 7 row and the multiples of 9 row on the chart. The equivalent fractions are 7/9, 14/18 , 21/27 , 28/36 , and so on.)
Display the Benchmark Fractions Number Line Master from Lesson 1. Direct students' attention to Question 6C.
- Who would like to show how to use common denominators to solve 2/5 + 3/8? (Possible response: I listed equivalent fractions for each fraction and chose fractions with 40 as a common denominator. I rewrote 2/5 + 3/8 as 16/40 + 15/40 = 31/40 .)
- Is this answer in simplest form? How do you know? (yes; I can't find a common factor to divide both 31 and 40 by in order to reduce the fraction.)
- Explain how you can find where 31/40 is on the fraction benchmark number line. (Possible response: 20/40 is 1/2, so 31/40 is more than 1/2.)
- Is 31/40 closer to 1/2, closer to one whole, or right in between the two? (Possible response: 1/2 is 20/40 and 1 is 40/40 , so 31/40 would be right in the middle of 1/2 and 1, like 3/4.)
Direct students' attention to Question 6D.
- Who would like to show how to use 48 as the common denominator when solving 7/8 − 5/6? (Possible response: You can multiply the denominators together and use 48 as the common denominator. 7/8 = 42/48 and 5/6 = 40/48 . 42/48 − 40/48 = 2/48 .)
- Is 2/48 in simplest form? (No, 2/48 is not in simplest form. See Content Note on simplest form.)
- Can you decide where 2/48 is on the fraction benchmark number line? (Possible response: I think of only 2 parts out of 48 parts, so 2/48 is very close to 0.)
- Did anyone use a lower common denominator in this problem? Explain. (Possible response: Yes; 24 is a lower common denominator. 21/24 − 20/24 = 1/24 .)