Students use a variety of models to explore fraction operations and are introduced to a variety of strategies to solve problems. Do not let this overwhelm you or your students. It is not expected that students become proficient in using all of the models. Students will gravitate toward and use what makes sense to them. Exposing students to many models and solution strategies will give them more ways to understand and solve complex problems.
Model the Multiplication. Throughout the lesson, students will model fraction multiplication. Begin by having students model the multiplication described in word problems. Modeling multiplication is important so that students can develop a good understanding of the concepts before they move on to standard algorithms. Models also help with estimation by showing that products can be quite a bit smaller than either of the fractions used, or if the fractions are both close to 1, that the product is then also close to 1. Present the following problem and ask students to solve it in pairs:
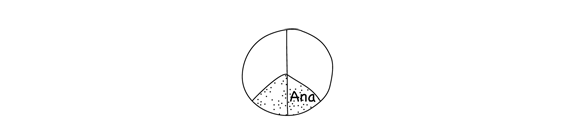
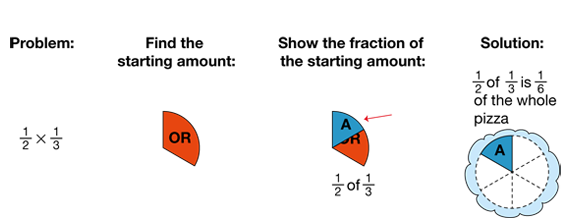
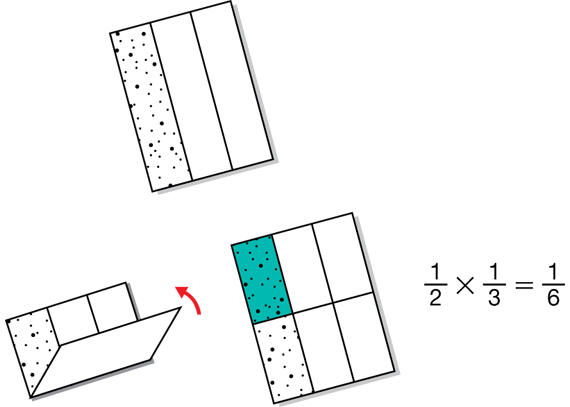
At the end of Luis's party, there is 1/3 of a pizza left. If he gives 1/2 of the leftover pizza to Ana, how much of the whole pizza will she get?
- Think about Ana's part of the whole pizza: 1/2 of 1/3. Will it be more than 1/2 or less than 1/2? Will it be more or less than 1/3? (Ana's share will be less than 1/2 and less than 1/3 of the whole pizza.)
- Think about the size of the product: 1/2 × 1/3. Will it be more than 1/2 or less than 1/2? Will it be more or less than 1/3? How do you know? (Possible response: I drew a picture to help me estimate. 1/2 × 1/3 will be less than 1/2 and less than 1/3.) [See Figure 1.]
Encourage student pairs to use whatever drawing or model will help them solve the problem. It is important for students to use strategies that make sense to them.
- Who would like to show how they solved the problem? (Possible response: I used fraction circle pieces. I put down an orange piece, 1/3 of a whole red piece, to represent the leftover pizza. Ana's share was 1/2 of the orange piece, an aqua piece, or one-sixth of the whole.) [See Figure 2.]
- Did anyone solve this problem a different way?
(Possible response: I used a strip of paper.)
[See Figure 3.]
If no one suggests it, use fraction circle pieces as shown in Figure 2 to model the problem before moving on to this next model.
- What is a number sentence that describes this problem? ( 1/2 × 1/3 = 1/6 )
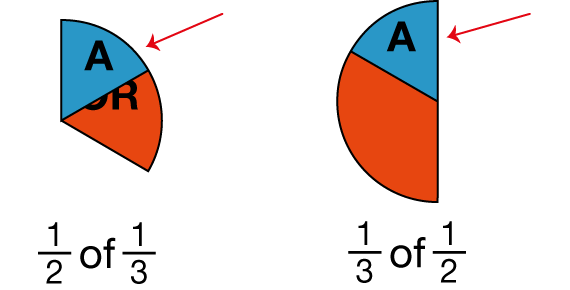
- Is 1/2 of 1/3 equal to 1/3 of 1/2? Is 1/2 × 1/3 = 1/3 × 1/2? How can you prove it? (See Figure 4 for a possible response.)
Fold Paper to Find Products. In this part of the lesson, students use paper folding to find the following products:
1/2 × 1/3
2/3 × 5/8
3/4 × 2/3
Explain to students that you are going to show them how to use paper folding to investigate the multiplication of fractions. Distribute several sheets of paper to each student. They will also need two colors of crayons or colored pencils. Demonstrate how to find the product of two fractions using paper folding as shown in Figure 5.
To multiply 1/2 × 1/3, instruct students to follow these steps:
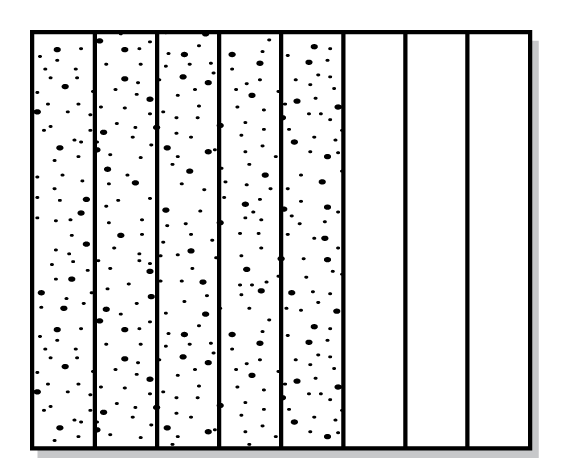
- Fold your paper in thirds lengthwise.
- Unfold the paper, trace the folds, and shade 1/3 using one color.
- Now fold the same paper in half horizontally.
- Unfold the paper, trace the fold, and use a different color to shade 1/2 of the colored 1/3 section.
- The fraction colored with both colors is 1/2 of 1/3.
When students complete the paper folding, ask:
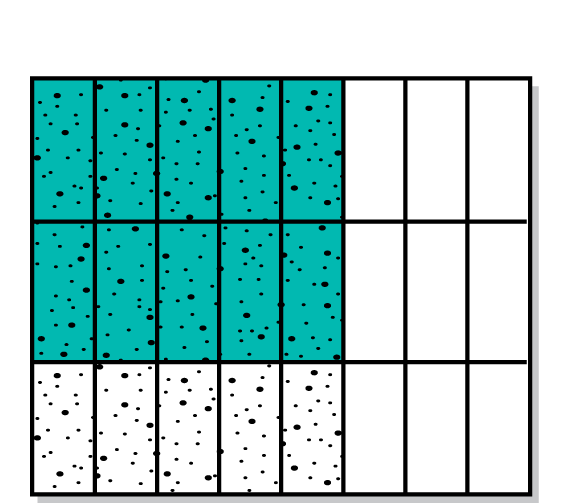
- How many parts is the whole paper divided into? (6)
- How many parts are shaded with both colors? (1)
- What fraction of the whole sheet of paper is 1/2 of 1/3? (1/6)
- What number sentence shows the product of 1/2 and 1/3? (1/2 × 1/3 = 1/6)
- Is 1/2 of 1/3 greater than or less than 1/3? Why? (less, because you are finding a part of 1/3)
To find 2/3 × 5/8, see Figures 6–7 and instruct students to follow these steps using a new piece of paper:
- Fold the paper into eighths lengthwise by folding it in half (2 parts), then in half again (4 parts), and then in half one more time (8 parts).
- Unfold the paper, trace the folds, and color 5/8. (See Figure 6.)
- Fold your paper into thirds horizontally.
- Unfold the paper, trace the folds, and color 2/3 of the 5/8 using a different color. (See Figure 7.)
- Count the total number of parts shown on the paper and count the number of parts that were colored twice. (24 total parts; 10 parts that are colored twice)
- What is a number sentence for the product of 2/3 and 5/8 ? Do not reduce the answer to simplest form. (2/3 × 5/8 = 10/24 )
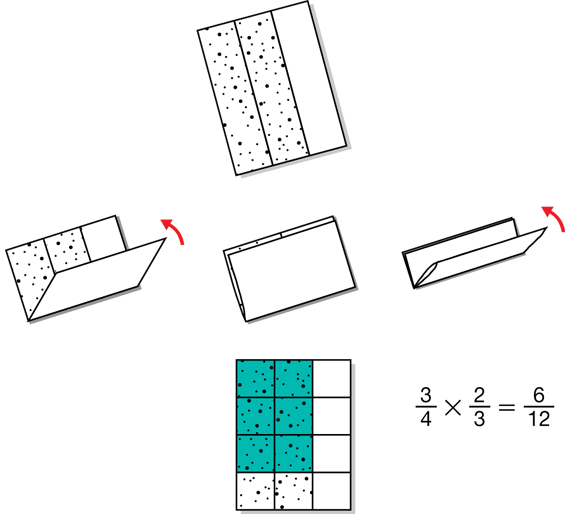
Continue to use paper folding to find 3/4 × 2/3. See Figure 8.
Instruct students to use another piece of paper and follow these steps:
- Fold your paper in thirds lengthwise.
- Unfold the paper, trace the folds, and shade 2/3 using one color.
- Fold your paper in half horizontally, then in half again to make fourths.
- Unfold the paper, trace the folds, and use a different color to shade 3/4 of the colored 2/3 section.
- Count the total number of parts shown on the paper and count the number of parts that were colored twice. (12 total parts; 6 parts that are colored twice)
- What is a number sentence for the product of 3/4 and 2/3 ? Do not reduce the answer to simplest form. (3/4 × 2/3 = 6/12 )
Display the number sentence 3/4 × 2/3 = 6/12 and ask:
- Is the product 6/12 reasonable? How do you know? (Yes, because the product 6/12 is equivalent to 1/2, which is less than 2/3. It should be less because I am only finding a part of 2/3.)
Write the resulting number sentences without reducing the answers to simplest form:
1/2 × 1/3 = 1/6
5/8 × 2/3 = 10/24
3/4 × 2/3 = 6/12
Ask questions such as the following:
- Do you see any patterns in the number sentences?
- Is this a pattern that is true for the other examples?
- Is there a pattern for how the number of parts (the numerator) is found?
Some students will begin to see that to multiply fractions, you can multiply the numerators and denominators as shown here:
3/4 × 2/3 = 3 × 2/4 × 3 = 6/12
Connect Models and Procedures. Display and direct students to the Multiply Two Fractions pages in the Student Guide. Discuss the problem and each solution strategy for solving 3/4 × 2/3 as presented in detail on the page. Nicholas models and solves the problem using fraction circle pieces. Discuss Question 1, which focuses on using estimation to check the reasonableness of a product.
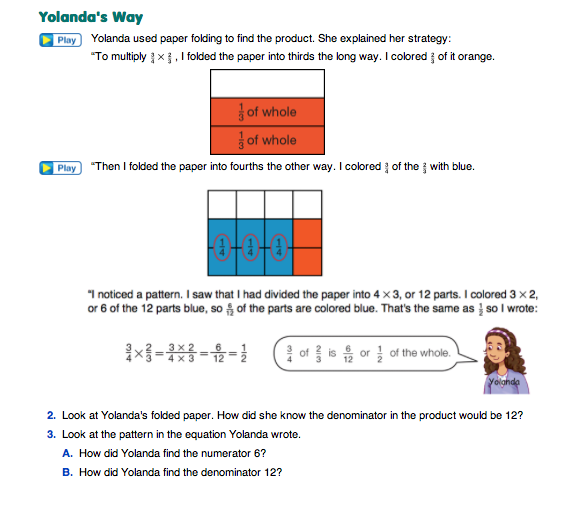
Yolanda uses paper folding. She explains that the paper is divided into 4 × 3 or 12 parts. 3 × 2 or 6 of those parts are colored twice. The discussion connects the paper folding with a paper-and-pencil procedure for multiplying fractions. Discuss Questions 2–3 and how the numbers in the paper-and-pencil procedure connect to the parts in the paper model.
Roberto sketches a rectangle model and uses a strategy like Yolanda's. Point out to students that even if their drawings do not have perfectly equal shares, they can still be used to count the parts and solve multiplication problems. Discuss Question 4 to help students make connections between the rectangle model and the paper-and-pencil procedure. In each situation, emphasize that the product of 3/4 × 2/3 is 6/12 (or half) of the whole circle or rectangle.
After discussion, assign Questions 5–8. Students solve problems using a variety of ways. As students work, they may notice that it is possible to multiply numerators and denominators to find the product before writing the answer in simplest terms. Using area models to solve these problems allows students to make connections to the numbers in the standard algorithm and create a deeper understanding of the paper-and-pencil procedures. As they begin using paper-and-pencil procedures, remind students to use estimation or to solve the problem a second way to check the reasonableness of their answers. Encourage students to use fraction circle pieces, drawings, paper folding, or any other model that will help them find and check the products. Encourage reasoning. For example, in Question 8F, students may reason that since 1/3 of 3 is 1, 1/3 of 3/10 is 1/10. When the class discusses solutions to the problems, ask them to discuss strategies for determining the reasonableness of their answers.
Share Solutions and Strategies. When most students have completed the questions, discuss their solutions for the problem in Question 7. Be sure to make connections between the different procedures and models.
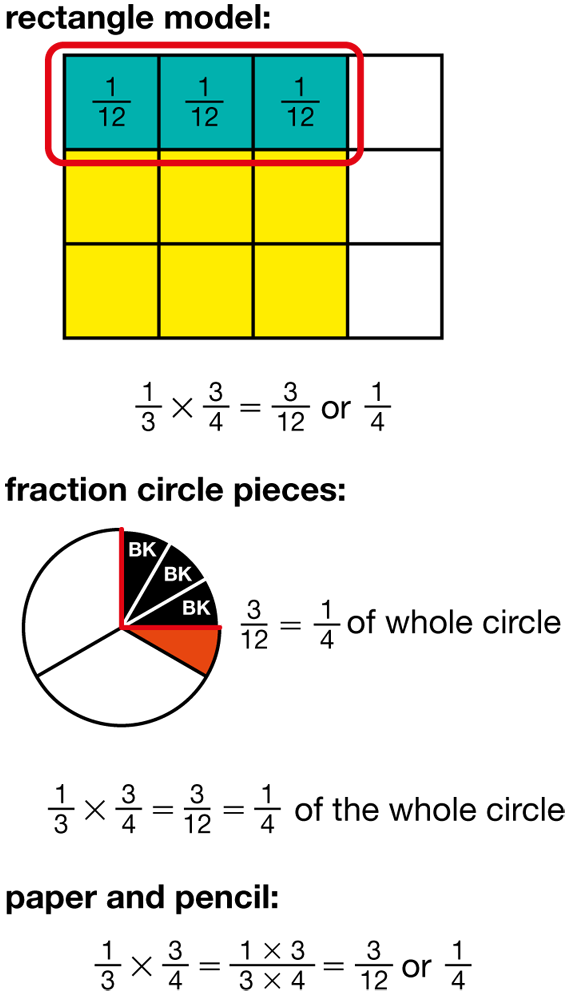
- How did you estimate the product of 1/3 and 3/4 ? Is it greater or less than 1/3? Is it greater or less than 3/4? (Possible response: The answer is less than 3/4 because we are finding a part of 3/4. Since we know that 1/3 × 3/4 = 3/4 × 1/3, the answer will also be less than 1/3 because we are finding a part of 1/3.)
- Who can show how to use a rectangle to solve 1/3 × 3/4? (See Figure 9.)
- Is this answer reasonable? How do you know?
(The answer is reasonable because 3/12 is 1/4 and that is less than 1/3 and less than 3/4.)
- Did anyone use fraction circle pieces? Show us.
(See Figure 9.)
- Who would like to show how to use paper and pencil to multiply 1/3 × 3/4? (See Figure 9.)
Give students a new problem and ask them to use a paper-and-pencil procedure. As students focus on using patterns and learn to use the algorithm, be sure to emphasize the meaning of what they are doing.
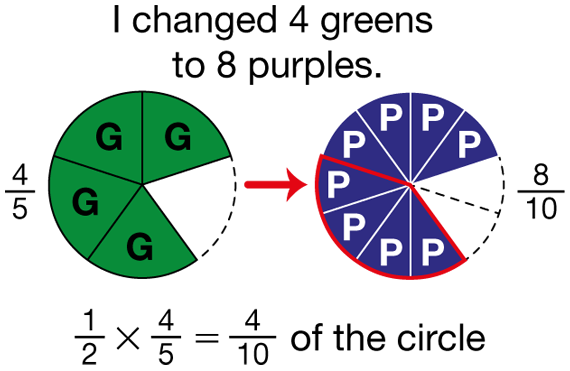
- Who would like to demonstrate how to use a paper-and-pencil procedure to solve 1/2 × 4/5? Show us. (Multiply the numerators, 1 × 4 = 4, and multiply the denominators, 2 × 5 = 10. 1/2 × 4/5 = 4/10.)
- Who would like to show how to solve the problem another way so that we can check the answer? (Possible response: Using fraction circle pieces, 10 purples cover a whole, so 5 purples cover a half. 4/5 of a pink half is 4 purples. 4 purples are 4/10 of the whole. 1/2 × 4/5 = 4/10.) [See Figure 10.]
- Is there another way to solve and check 1/2 × 4/5? (I used a number line.) [See Figure 11.]
Use Check-In: Question 9 on the Multiply Two Fractions pages in the Student Guide to assess students' abilities to represent multiplication of fractions with area models, number sentences, or drawings [E3]; multiply fractions using area models or paper-and-pencil procedures [E4]; and check for reasonableness [MPE3]. Use the Workshop in Lesson 11 to provide targeted practice.