Solving Fraction Multiplication Problems

Est. Class Sessions: 2

Developing the Lesson

Model the Multiplication. Present this word problem to students:

One-half of the guests at Luis's party were relatives. Three-fifths of the relatives were cousins. What fraction of his guests were cousins?

Ask:

Think about the size of the product. Will it be more or less than 1/2?
Will it be more or less than 3/5?

Help students understand and visualize the multiplication in the problem by modeling it. To find 3/5 of 1/2, first display a pink half.

Demonstrate the process as you ask:

What “half” is referred to in the word problem? (One-half of the guests at Luis's party were relatives.)
If this pink piece represents half, what piece represents the whole? (1 red circle)
What is the whole being referred to in the word problem? (the guests at Luis's party)
What are you trying to find 3/5 of? (3/5 of 1/2 of the guests)
How can I show 3/5 of 1/2? What pieces can I use to divide the pink piece into fifths? (Purples will divide the half into 5 equal parts. 3 purples show 3/5 of the half.)

Place 5 purple pieces onto the pink piece, and then remove 2 purple pieces to show 3/5.

Think back to the whole. Three purple pieces are what fraction of the whole? (3/10)
What number sentence can you write to describe this problem? (3/5 × 1/2 = 3/10)
What does an answer of 3/10 mean in this word problem? (3/10 of all the guests at the party were cousins.)
Does this answer make sense? How do you know? (Yes; the product of 3/5 × 1/2 is 3/10. Three-tenths is less than 3/5 and is also less than 1/2 since you are finding a part of a fraction.)
Can anyone solve 3/5 × 1/2 a different way? (Possible response: 3/5 is 1/5 + 1/5 + 1/5. Half of that is 1/5 + 1/10. 2/10 + 1/10 = 3/10.)

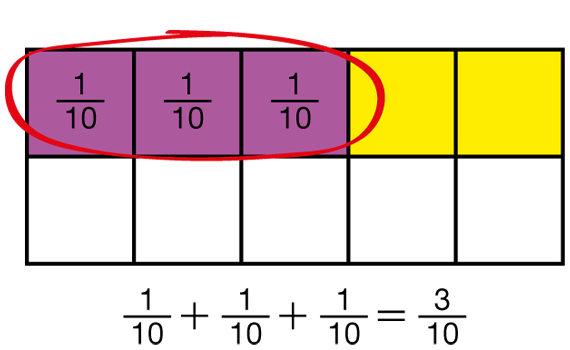
Ask a student to demonstrate how to check the problem by solving it with a rectangle model. See Figure 1.

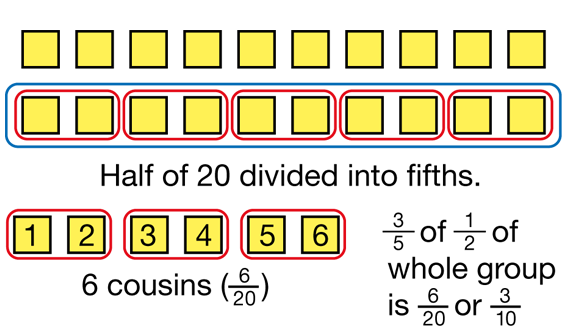
Model with Counters. Multiplication of fractions such as 3/5 × 1/2 can be modeled with connecting cubes or any counters; however, students may need help finding ways to determine the whole. Tell students a similar problem in which the whole is given:

There were 20 guests at Luis's party. Remember, one-half of the guests were relatives. Three-fifths of the relatives were cousins. What fraction of his guests were cousins?

Guide student pairs as they use 20 connecting cubes to model the problem. Demonstrate the process using a display set of connecting cubes. See Figure 2.

Ask:

One-half of the guests were relatives. Show 1/2 of the cubes. How many cubes are in one-half? (10 cubes)
Now divide this half (10 cubes) into five equal groups (fifths). How many cubes are in one-fifth of one-half of the whole group? (2 cubes)
How many cubes are in three-fifths of one-half? (6 cubes)
What fraction of the whole group is 6 cubes? What fraction of the guests were cousins? (6/20)
What is 6/20 in simplest form? (3/10)

Display the number sentence 3/5 × 1/2 = 3/10. Take the problem further by asking students to review multiplying a fraction by a whole number.

Ask:

If 3/10 of 20 guests are cousins, how can you figure out how many of the guests were cousins? (3/10 × 20 = 60/10 ; 6 of the 20 guests were cousins.)
In your opinion, which is easier to understand or picture: 3/10 of the guests are cousins or 6 of the guests are cousins? (Possible response: 6)
How did the counters help you “see” the 6 guests? (I can see the 6 counters. Each counter represents one cousin.)
Could we solve this same problem with another strategy or tool? (yes, with paper folding or fraction circle pieces)
Can you “see” the 6 as easily with the other strategies? (no; the product is 3/10 of the group is cousins. We know the fraction but in order to see that it is 6 people, we have to solve 3/10 of 20.)

Remind students that some strategies are more appropriate for some problems than others. A goal is to have many ways to understand and solve problems so that you can choose appropriately from the variety of strategies.

Solve Fraction Multiplication and Area Problems. Display and direct students to the Solving Fraction Multiplication Problems pages in the Student Guide. The following problem is presented:

The Happy Birthday sign at Luis's party was 21/4 feet long and 7/8 feet wide. What is the area of the rectangular sign?

Assign Questions 1–3. In Question 1, students work with a partner to find the area of the sign. Upon completion of the questions, discuss a few students' solution strategies. Remind students to use square units when reporting area. Using a display of Question 2 the Solving Fraction Multiplication Problems page, discuss Mark's solution. He partitions a rectangle, computes the partial products, and finds the area of the rectangular sign.

Discuss Question 3 and ask:

Do you have to find an exact product for Question 3, or can you answer the question with estimation? Explain. (Possible response: I can estimate. 131/32 sq. ft. is very close to 2 square feet. With 6 square feet of paper, Luis's sister can make 3 signs.)

Assign Questions 4–18. In Question 4, students find the area of small rectangles like Mark did in the example problem. In Question 5, students solve equations involving fraction multiplication. Students solve fraction multiplication word problems in Questions 6–18 using any strategy they like. Some problems simply require estimation. Encourage students to draw pictures, use fraction circle pieces, fold paper, sketch rectangles, or use a paper-and-pencil method to find products. Remind them to include number sentences and labels in their answers.