Lesson 4

Measure with Unusual Units

Est. Class Sessions: 3

Developing the Lesson

Part 1: Measuring with Different Units of Measure

X

Measurement Error and Mistakes. Any measurement in the real world is an approximation because any measuring instrument has a limit to its accuracy. For example, a centimeter ruler can only measure to the nearest tenth of a centimeter, so it cannot be used to measure an object accurately to the nearest hundredth of a centimeter. On the other hand a mistake usually refers to an error that arises because of human carelessness, inattention, or misunderstanding.

When teaching, it is important to be aware of this distinction. Measurement error will occur, i.e., different students measuring the same object with the same unit will sometimes reach slightly differing results, even when using correct procedures. On the other hand, if two students get widely differing measurement results, it is most likely the result of a mistake, i.e., misunderstanding or using incorrect procedures. In these instances, it is necessary to draw attention to the possible causes of the mistake so that the errors in method or understanding may be addressed.

Review Measurement Advice. Ask students how they can measure the length of an object using different measuring tools.

For example, ask:

X
  • How can you measure a pencil using paper clips?

Display a pencil and paper clips. Prompt the discussion by leaving gaps between the paper clips, using large and small paper clips, and arranging the paper clips in a zig-zag fashion.

Ask:

X
  • What's wrong with this way of measuring? (Possible responses: There is space between the paper clips; they are not in a straight line; the paper clips are not the same size.)
  • What will happen if I measure this way? (You will not get an accurate measurement.)
  • Why do you think so?

Display the Measuring Advice chart from Lesson 2. Review the suggestions already posted. Add to the list as different points come up in the discussion.

Guide the discussion to focus on these central ideas:

  • Measurements need to be reported as both the number of units and the kind of unit (e.g., 7 small paper clips).
  • Measurements should be made with units that are all the same; switching from large paper clips to small paper clips, for instance, is not a good idea.
  • Units should be placed end to end—no overlaps or gaps.
  • Units should be placed, as nearly as possible, in a straight line.
  • Sometimes a measurement includes a part of a unit. Let students decide how they will handle such measurements. Some may prefer "between 7 and 8 paper clips," while others may say "closer to 8 paper clips" or "almost 8 paper clips."

Measure a Desk with Unusual Units. Display the Measuring with Unusual Units chart you prepared prior to the lesson. See Materials Preparation. Show students you have listed the four nonstandard units of measure on the data table. Distribute two different sets of nonstandard units you prepared to each student group. Make sure that each group receives two containers of measuring objects that are of noticeably different size, such as a box of connecting cubes and a box of clothespins. The difference in measurement should be easy to identify. Each group will measure the length of a desk using these two different objects, once using the smaller unit of measure and once using the larger unit of measure. Give each student group two self-adhesive notes on which they will record their two measurements.

X

If the desks in the classroom vary in size, make sure groups measure desks of the same size or choose another common length (e.g., length of a book, floor tile, or table).

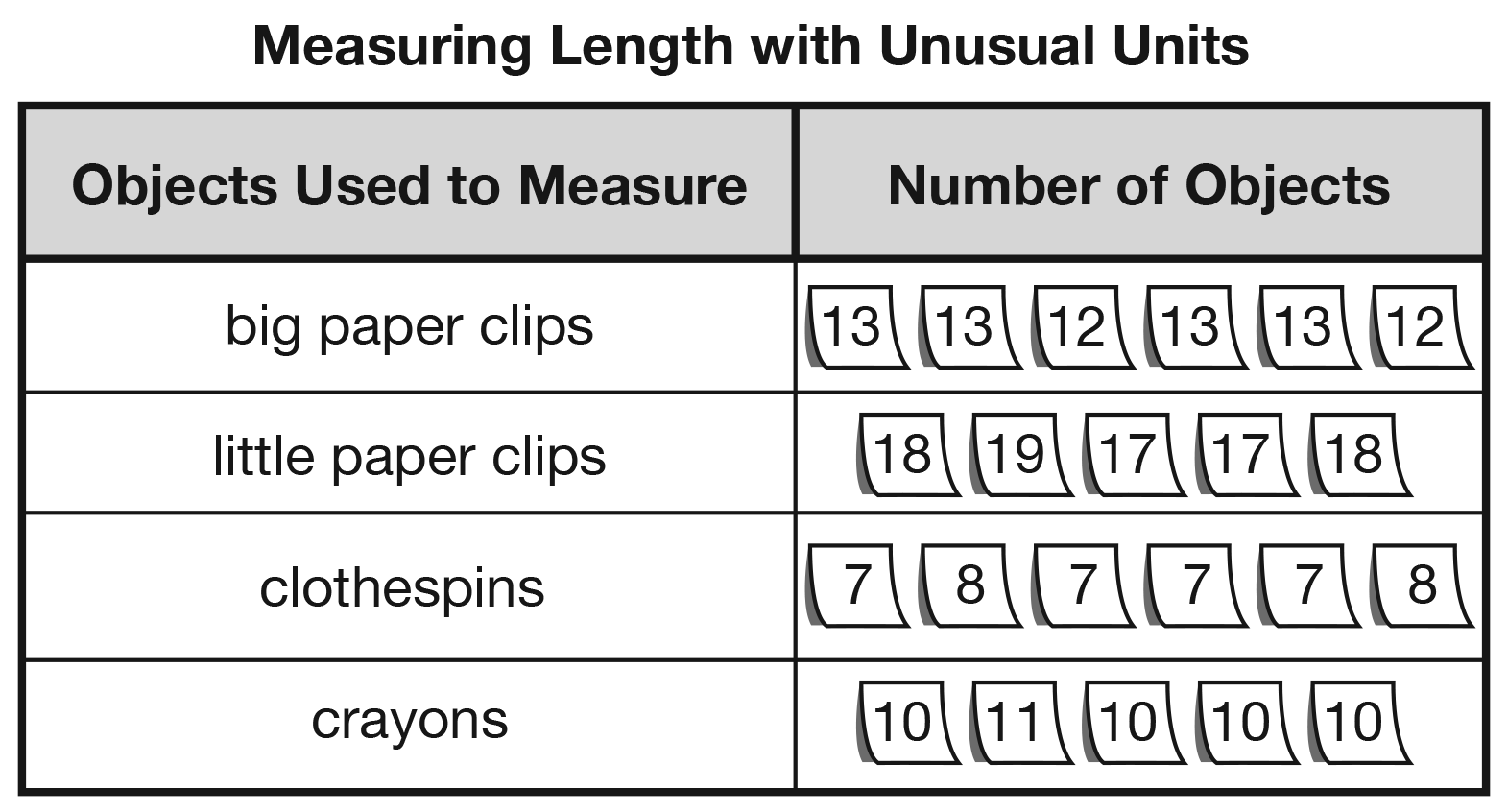
Record Data on Chart. After each group measures the length of a desk twice, have them place their selfadhesive notes in the Number of Objects column next to the appropriate object on the Measuring Length with Unusual Units chart. See Figure 3 for an example chart.

The groups that measured the desk with the same unit of measure should have the same or very close results. If this does not happen, ask how the differences might be handled. Students might suggest measuring again. Others may point out that different groups dealt differently with partial units. If there are significant differences in measurements using the same unit, it may be necessary to refer back to the Measuring Advice chart to correct erroneous techniques and understandings. Before beginning the graph, decide on one measurement for each object used.

Ask:

X
  • What is the most common measurement when [big paper clips] were used? How did you decide?

Remove all the self-adhesive notes and record the one agreed-upon measurement for each of the four objects used to measure in the Number of Objects column.

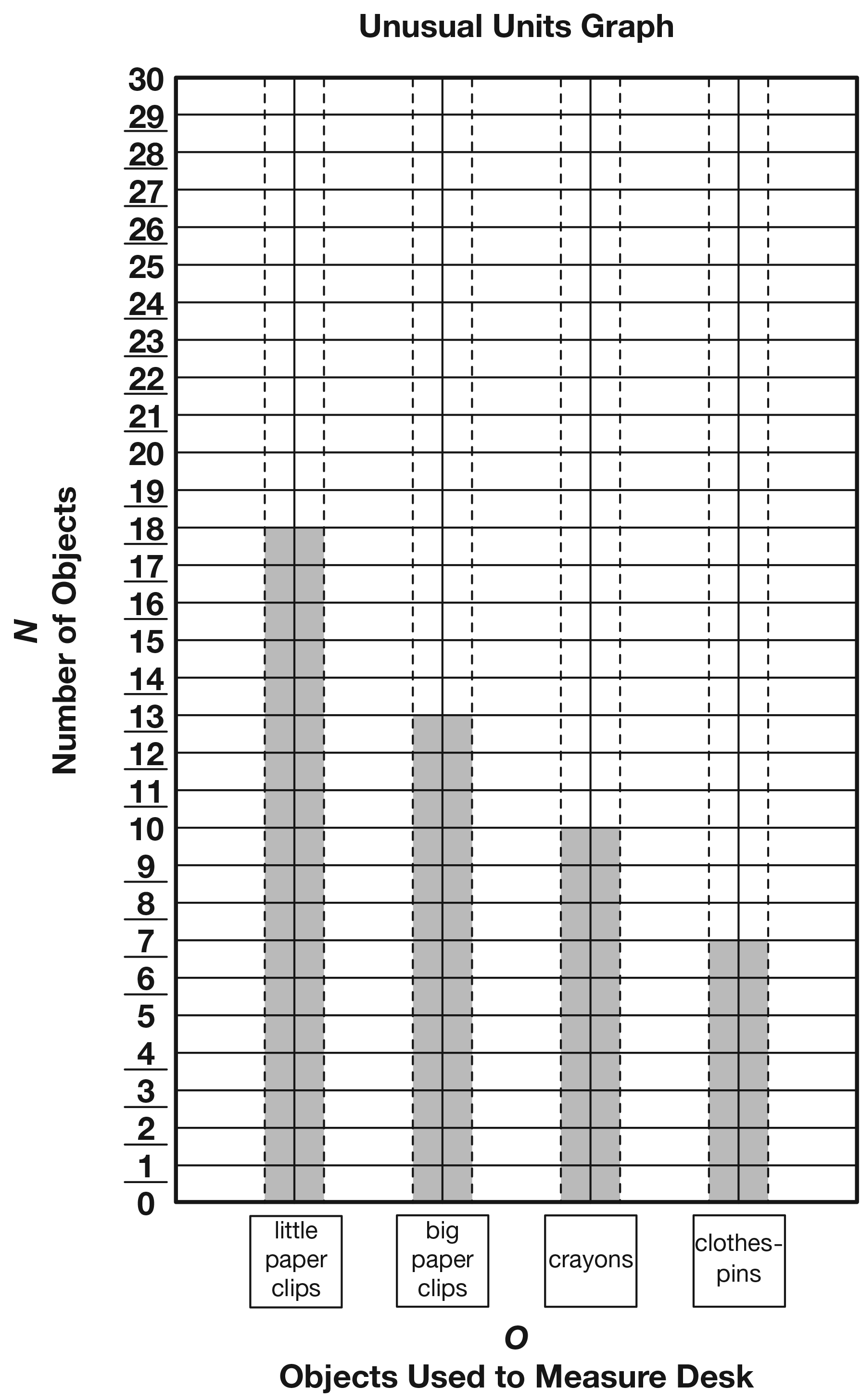
Display the Unusual Units Graph Master. List the objects used as measuring units from shortest to longest along the horizontal axis of the graph.

Ask:

X
  • What do you notice about the numbers on this graph? (The vertical axis is numbered by fives. The other numbers are missing.)
  • This axis is like a number line with some numbers missing. Count by ones as I touch each line on the vertical axis.
  • Where would you find 11 on this axis? 17? 4? (Have volunteers point to the line on the graph.)

Have student volunteers assist you by filling in the bars on the graph. See Figure 4 for a sample graph.

X

If you feel that students' understanding and involvement would benefit from their having their own graph, make copies of the completed class graph you created on the Unusual Units Graph Master for each student.

Adventure Book:
Student Activity Book:
Master:
Example of collecting class data on chart
X
+
Sample graph
X
+