Z. Planet Gzorp 


The drawings show the growth of a creature from Planet Gzorp.

- Use square-inch tiles or grid paper to build models or draw pictures of this creature up to at least age 6. As you add squares to each year of age, record the data in a table. Put Age in Years (A) in the first column and Size in Squares (S) in the second.
- Draw a 4-year-old creature. Name your creature.
- Graph your data. Use graph paper or a computer.
- At what point does the line or curve meet the vertical axis? What does it mean about your creature when it was born?
- Look at the table and graph. Describe any patterns you see. Think about going down the columns and across the rows.
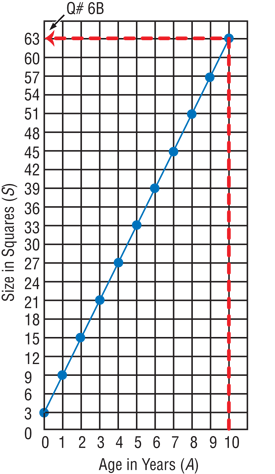
- How many squares (S) does the creature have when it is the following ages (A)? Show or tell how you find each age in years.
- 7 years
- 10 years
- 20 years
- 25 years
- Describe a rule in words for finding the size in squares (S) for a creature of any age (A). Write a formula using symbols.
- Use your formula to find the size of the creature when it is 25 years old. Is the answer the same as 6D?
- How old is the creature when it has 603 squares? Show or tell how you know.