Assessment in this unit
Key Ideas, Expectations, and Opportunities
Using Assessment to Meet Individual Needs
The explicit Expectations and assessment tasks in this unit
describe what it means to "get it." Providing feedback on these
Expectations helps identify students who need to access the
content another way, need further practice opportunities, or are
ready to extend or deepen their understanding of a concept.
Instructional opportunities that help support the varied needs of
students also need to be identified. These opportunities provide
models that can be replicated or used multiple times and can be
used in a variety of settings (e.g., home, transitions, support
classroom, as a center).
The Assessment Program serves the
following purposes:
- It provides information to teachers about what students
know and can do. This information is used to guide instruction.
An activity may help teachers answer questions about whole-class
instruction: What do I do next? In the next minute? Next lesson?
Next class? Next unit? Other assessments may help teachers decide
how to support individual students, including those who struggle
with a concept and those who are ready to be challenged.
- It communicates the goals of instruction to parents and
students. What teachers choose to assess communicates to the
class what they value. For example, if teachers want students to
work hard at communicating problem-solving strategies, then it is
important to assess mathematical communication.
- It provides feedback to students and parents about
student progress. This includes teacher evaluation of student
progress as well as students' assessment of their own progress.
Key Mathematical Ideas
The mathematical content in Math Trailblazers is organized
around a set of Key Ideas. These Key Ideas are based on the National
Council of Teachers of Mathematics (NCTM) Standards for the
grade band as well as current thinking in the mathematics education
community, e.g., Charles (2005), NCTM (2000), Van de Walle (2013).
There is a set of Key Ideas for each content strand: Number, Algebra,
Geometry, Measurement, and Data. They are based on "big ideas" in
mathematics and describe what students should be able to do within
each strand. The Key Ideas are shown in the table in Figure 1.
| 1. Number Sense:
Understand the base-ten number system, recognize relationships
among quantities and numbers, and represent numbers in multiple
ways. |
2. Operations: Understand the meaning
of numerical operations and their application for solving
problems. |
3. Computation and
Estimation: Use efficient and flexible procedures to compute
accurately and make reasonable estimates. |
|
| 1. Identifying Patterns:
Identify and describe patterns and relationships, including how a
change in one variable relates to a change in a second variable. |
2. Tables and Graphs:
Represent patterns and relationships with graphs, tables, and
diagrams. |
3. Symbols:
Represent patterns and relationships with symbols (includes using
variables in formulas and as unknowns in equations). |
4. Using
Patterns: Apply relationships, properties, and patterns to solve
problems, develop generalizations, or make predictions. |
| 1. Shapes: Identify, describe, classify,
and analyze 2- and 3-dimensional shapes based on
their properties. |
2. Orientation and Location: Use
coordinate systems to specify locations and describe spatial
relationships. |
3. Motion: Apply transformations (slides,
flips, and turns) and use symmetry to analyze mathematical
situations. |
4. Geometric Reasoning: Use
visualization, spatial reasoning, and geometric modeling to solve
problems. |
| 1. Measurement Concepts:
Understand measurable attributes of objects or situations (length,
area, mass, volume, size, time) and the units, systems, and
processes of measurement. |
2.
Measurement Skills: Use measurement tools, appropriate
techniques, and formulas to determine measurements. |
| 1. Data Collection: Select, collect, and
organize data to answer questions, solve problems, and make
predictions. |
2. Data Representation: Select and create
appropriate representations, including tables and graphs, for
organizing, displaying, and analyzing data. |
3. Data Description: Describe a data set
by interpreting graphs, identifying patterns, and using
statistical measures, e.g., average and range. |
4. Using Data: Apply relationships and
patterns in data to solve problems, develop generalizations, and
make predictions. |
Figure 1: Key Ideas for Math
Trailblazers (Key Ideas
addressed in Unit 6 are shaded.)
Expectations
To monitor students' growth across and within grades, there are
a set of Expectations that describe what students are
“expected” to do within each content strand. Expectations
show the growth of the mathematical content within the Key Ideas for
each strand.
| EXPECTATIONS |
|
Use this list of Expectations to assess students on the
key concepts and skills in this unit. |
| E1* |
Represent two-digit and three-digit numbers using base-ten
pieces, number lines, and symbols. |
| E2* |
Compose and decompose numbers using ones, tens, and
hundreds. |
| E3* |
Show and recognize different partitions of numbers using
different representations (base-ten pieces, number lines, number
sentences). |
| E4 |
Make connections between place value concepts and
representations of numbers (e.g., base-ten pieces, number lines,
number sentences, symbols). |
| E5* |
Recognize that different partitions of a number have the
same total (e.g., 50 + 4 = 40 + 14). |
| E6 |
Estimate a quantity using 10 and 100 as benchmarks. |
| E7 |
Use words and symbols (e.g., <, >, =) to show comparisons
of quantities. |
| E8 |
Compare and order three-digit numbers using base-ten
pieces and a number line. |
| E9 |
Tell and write time from an analog clock to the nearest
five minutes. |
| E10* |
Demonstrate fluency with the addition facts in Groups C (1 + 9, 2 + 7, 2 + 8, 2 + 9,
3 + 6, 3 + 7, 3 + 8, 4 + 6, 4 + 7, 5 + 5, 5 + 6)
and Group D (3 + 3, 3 + 4, 4 + 4, 4 + 5, 6 + 6, 6 + 7, 7 + 7, 7 + 8, 8 + 8,
10 + 4, 10 + 10). |
| E11* |
Determine the unknown number in an addition or subtraction
sentence relating three whole numbers for the facts in Groups C
and D. |
Targeted Practice
This unit provides opportunities for additional targeted
practice for some of the Expectations. See the chart in Figure 3 and
the descriptions that follow. These opportunities connect directly to
assessment tasks, so the practice can be tailored to the current
level of student progress.
- For students who are struggling with the Expectation,
practice is targeted toward the foundational concepts and skills
involved and often provides a different way to access the content.
- For students who are making significant progress toward the
Expectation, practice is designed to help move toward proficiency
and autonomy.
- For students who are already meeting the Expectation,
opportunities are provided to deepen or extend understanding.
| Expectation |
Opportunities for Targeted Practice |
| E1*. |
Represent 2-digit and 3-digit numbers using base-ten
pieces, number lines, and symbols. |
|
| E2*. |
Compose and decompose numbers using ones, tens, and
hundreds. |
|
| E3*. |
Show and recognize different partitions of numbers using
different representations (base-ten pieces, number lines, number
sentences). |
|
| E4. |
Make connections between place value concepts and
representations of numbers (e.g., base-ten pieces, number lines,
number sentences, symbols). |
|
| E5*. |
Recognize that different partitions of a number have the
same total (e.g., 50 + 4 = 40 + 14). |
|
| E6. |
Estimate a quantity using 10 and 100 as benchmarks. |
|
| E8. |
Compare and order three-digit numbers using base-ten
pieces and a number line. |
|
| E10*. |
Demonstrate fluency with the addition facts in Groups C (1 + 9, 2 + 7, 2 + 8, 2 + 9, 3 + 6, 3 + 7,
3 + 8, 4 + 6, 4 + 7, 5 + 5, 5 + 6) and Group D (3 + 3, 3 + 4, 4 + 4, 4 + 5,
6 + 6, 6 + 7, 7 + 7, 7 + 8, 8 + 8, 10 + 9, 10 + 10). |
|
| E11*. |
Determine the unknown number in an addition or subtraction
sentence relating three whole numbers for the facts in Groups C and
D. |
|
Figure 3: Expectations for Unit 6 with
opportunities for targeted practice
Workshop
Much of the targeted practice is in Lesson 7 Workshop: Place
Value Concepts, which provides a menu of activities that revisit key
concepts and skills developed earlier in the unit. Based on students'
self-assessment of their confidence with Expectations, students
select activities from a Menu. See Figure 4. Teacher guidance can
help students find the appropriate level of practice.
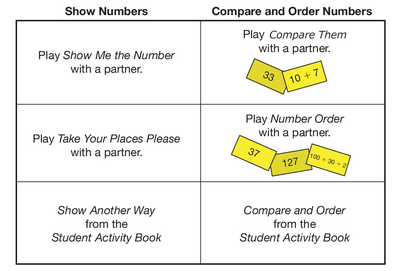
Figure 4: Workshop Menu from Lesson 7
) on the Unit 6
Key Assessment Opportunities Chart. See Figure 2. In this unit,
students will also become better acquainted with the Math Practices
Expectations by discussing them in the context of a specific problem
and receiving feedback.