Place Value
Developing Place Value
This unit continues students' work with place value of three-digit numbers by … read more
Developing Place Value
This unit continues students' work with place value of three-digit numbers by using the base-ten pieces. Activities lay conceptual groundwork for performing addition and subtraction. Two-digit addition and subtraction methods are developed in upcoming units.
In Unit 5, students snapped cubes together to make groups of ten. The act of snapping them together helped students become familiar with the idea of trading with the base-ten pieces. They used cubes to partition numbers, specifically into groups of ones, tens, and hundreds. They represented their partitions using number sentences.
In this unit, students revisit partitioning using base-ten pieces to further develop number sense. Base-ten pieces are used extensively to provide a concrete representation of the relationship between a digit's position and its value. This helps students understand how different digits in a number are used to represent different quantities.
Base-Ten Pieces
The base-ten pieces representing ones, tens, and hundreds are introduced here. … read more
Base-Ten Pieces
The base-ten pieces representing ones, tens, and hundreds are introduced here. In Grade 3, students will also work with the base-ten piece that represents one thousand. Each piece is given a nickname so that students and teachers can refer to the concrete materials separately from the numbers. See Figure 1. This eliminates confusion when distinguishing base-ten pieces from the written number they represent, e.g., three "skinnies" from three in the tens place. Using nicknames also provides flexibility to change the values of pieces when decimals are introduced. In grades 3 and 4, the flat is used as one whole, the skinny as one-tenth, and the bit as one one-hundredth.
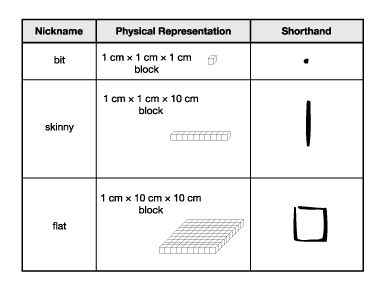
Figure 1: Base-ten pieces
A shorthand for drawing the blocks is shown in the table in Figure 1. The shorthand allows both teachers and students to sketch the pieces quickly. Students are introduced to the shorthand in Lesson 2.
The physical appearance of base-ten pieces is particularly well-suited for developing an understanding of the base-ten system (National Research Council, 2001). The ratios of the blocks' sizes are the same as the ratio of their corresponding values in the base-ten system. Working with base-ten pieces helps students visualize our number system's ten-for-one equivalencies. Each piece, once assigned a value, retains this value. The value of the piece is immediately known from its appearance.
Throughout the unit, in both class discussions and small group activities, students work with tables that show partitions of numbers and corresponding number sentences. See Figure 2.
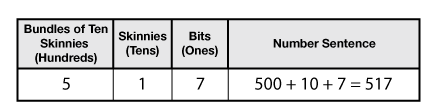
Figure 2: Recording the hundreds, tens, and ones
For example, by recording 2 in the skinnies column, students begin to understand that this 2 is different from recording 2 in the bits column. This 2 indicates two 10s, or 20. This develops the notion of the values of the places. When students have formed the connection between the blocks and numbers, they can easily form mental pictures of the blocks when solving problems. By recalling the blocks, students can make sense of regrouping when adding and subtracting. Then they can figure out for themselves the steps involved. Subsequently, they make fewer mistakes and regard mathematics as a subject that should and does make sense. Research shows that students who learn to add and subtract using base-ten pieces have a much greater understanding of place value than those who do not (Fuson and Briars, 1990).
Comparing Numbers
The relationship of the block sizes also makes base-ten pieces an ideal … read more
Comparing Numbers
The relationship of the block sizes also makes base-ten pieces an ideal tool for comparing numbers and developing number sense for larger numbers. Students can see that one or two of the large blocks will have many more units than the same number of smaller blocks. This visualization is especially powerful when used in conjunction with the number line. Students work with the concepts of equal to, greater than, less than and the corresponding notation ( =, >, and <).
Time
Students build on their previous work to develop strategies for telling time … read more
Time
Students build on their previous work to develop strategies for telling time to the nearest 5 minutes on the analog clock. Students explore the relationship and movement between the hour hand and minute hand as they develop these strategies.
Continue to frequently draw attention to the actual time on the classroom clock. As students go through their daily routines, make a point to note when activities start or end on the hour and half hour.
MATH FACTS and MENTAL MATH

Addition Facts
Daily Practice and Problems items in this unit can be used to… read more
Addition Facts
Daily Practice and Problems items in this unit can be used to assess students' fluency with the addition facts in Group C (1 + 9, 2 + 7, 2 + 8, 2 + 9, 3 + 6, 3 + 7, 3 + 8, 4 + 6, 4 + 7, 5 + 5, 5 + 6) and in Group D (3 + 3, 3 + 4, 4 + 4, 4 + 5, 6 + 6, 6 + 7, 7 + 7, 7 + 8, 8 + 8, 10 + 9, 10 + 10). The make ten strategy and the using doubles strategies are commonly used to solve these facts.
Related Subtraction Facts
Students have been connecting addition to subtraction and using the … read more
Related Subtraction Facts
Students have been connecting addition to subtraction and using the addition facts to solve subtraction problems. A student proficient with his or her addition facts can also find the related subtraction facts. Daily Practice and Problems items in this unit can be used to assess students' abilities to use the addition facts to solve the related subtraction problems for each fact in Group C and Group D.
Resources
- Fuson, Karen C., and D.J. Briars. “Using a Base-Ten Blocks Learning/Teaching Approach for First- and Second-Grade Place-Value and Multidigit Addition and Subtraction.” Journal for Research in Mathematics Education, 21 (3), pp. 180–206, 1990.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, (Eds.), pp. 181–229, National Academy Press, Washington, DC, 2001.
- Thompson, C.S., and J. Van de Walle. “A Single-Handed Approach to Telling Time.” Arithmetic Teacher, 28 (8), pp. 4–9, April 1981.
- Van de Walle, J.A., K.S. Karp, and J.M. Bay-Williams. Elementary and Middle School Mathematics: Teaching Developmentally Eighth Edition. Pearson Education, Inc., Upper Saddle River, NJ, 2013.












