lesson 4

Many Ways to Make a Number

Estimated Class Sessions: 2

Developing the Lesson

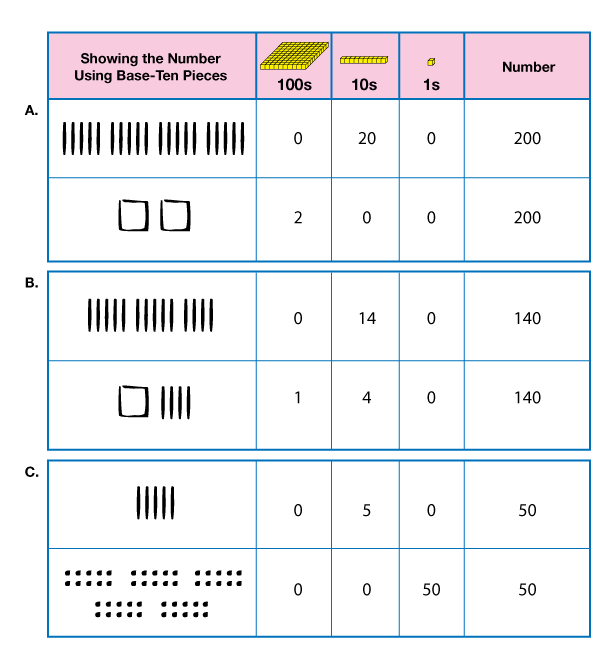
Represent Different Partitions of Numbers. Show a display of the Base-Ten Recording Sheet from the Student Activity Book. Present the problems given below one at a time, or make up similar ones. For each problem, student pairs build a model using their base-ten pieces. They use their models to make trades, fill in the Base-Ten Recording Sheet, and answer questions posed orally. As they answer, fill in the display of the Base-Ten Recording Sheet, using base-ten shorthand to draw the representation. Remind students about using a dot (•) to represent a bit, a vertical line ( | ) to represent a skinny, and a square ( ◻ ) to represent a flat. Work through the first problem as a class.

There is a small space between problems on the Base-Ten Recording Sheet to indicate when a new number is represented. See Figure 1 for an example. The problems gradually increase in difficulty.

Question A:

X
  • Take 20 skinnies. Draw them using base-ten shorthand.
  • Trade for flats. How many flats will you have? How many skinnies are left over? (2 flats, no skinnies left over)
  • How do you know? (10 skinnies make 1 flat; 20 is two tens, so 20 skinnies is 2 flats.)
  • Draw the flats. What will you write in the other spaces?
  • What number does 20 skinnies represent? How do you know? (200; counting by tens, I know that ten skinnies is 100; 100 + 100 = 200.)
  • What number do the 2 flats represent? How do you know? (200, 100 + 100 = 200)
  • Which representation of 200 shows the Fewest Pieces Rule, 20 skinnies or 2 flats? How do you know? (The two flats representation uses the fewest pieces. It uses only 2 base-ten pieces. When I had 20 skinnies, that was 20 pieces.)
  • What is a number sentence that matches the 2 flats? (100 + 100 = 200)
  • Circle the representation that shows the Fewest Pieces Rule. (two flats)

For the following problems, state the initial problem and give student pairs a few minutes to make their models. They work together to fill in the table for each problem. Then ask the remaining questions and ask students to fill in the table on the display. Have them circle the representation that shows the number using the Fewest Pieces Rule.

Question B:

X
  • Take 14 skinnies and trade for flats. How many flats will you have and how many skinnies left over? (1 flat and 4 skinnies left over; I trade 10 skinnies for the flat; 14 – 10 = 4; I cannot trade 4 skinnies for another flat so I have 4 skinnies left over.)
  • What number do you have? How do you know? (140; 1 flat is 100; skip counting by tens, 4 skinnies is 10, 20, 30, 40.)
  • Which representation shows the Fewest Pieces Rule, 14 skinnies or 1 flat and 4 skinnies? (1 flat and 4 skinnies)

Question C:

X
  • If you have 5 skinnies and you trade them for bits, how many bits would you have? How do you know? (50 bits; counting by tens on my 200 Chart, I count 10, 20, 30 ... five times and get to 50.)
  • Which representation shows the Fewest Pieces Rule, 5 skinnies or 50 bits? (5 skinnies)

Question D:

X
  • Take 11 skinnies and 4 bits. Trade 1 of the skinnies for bits. How many bits will you have altogether? How do you know? (14 bits; 10 + 4 = 14)
  • What is the number? (114) How do you know? (10 skinnies is 100; 100 + 14 = 114)
  • Which representation shows the Fewest Pieces Rule, 11 skinnies and 4 bits, or 10 skinnies and 14 bits? (Neither representation shows the Fewest Pieces Rule.)
  • Why? (More trades can be made in both representations.)

Question E:

X
  • Take 12 skinnies and 7 bits. Show this number using the Fewest Pieces Rule. What is the number? How do you know? (I trade 10 skinnies for 1 flat and I have 2 skinnies left over. With the 7 bits, I have 1 flat, 2 skinnies, 7 bits. I can't make any more trades, so I know I am using the Fewest Pieces Rule and it matches the number 127.)

Question F:

X
  • Take 7 skinnies and 16 bits. What trade can you make to show the fewest pieces? What is the number? How do you know? (I can trade 10 bits for 1 skinny. Then I have the fewest pieces. 8 skinnies and 6 bits or 86. 8 tens is 80 plus 6 more.)

Question G:

X
  • Take 1 flat, 12 skinnies and 15 bits. What trades can you make to show the Fewest Pieces? What number is this? (I trade 10 bits for 1 skinny and 10 skinnies for 1 flat. I have 5 bits, 3 skinnies, and 2 flats or 235.)

Connect Fewest Pieces to Place Value. Continue with similar problems for as long as seems appropriate or necessary so that your students have many opportunities to practice representing partitions of numbers and making trades. Help them to begin to see the advantage of representing a number using the Fewest Pieces Rule.

Ask:

X
  • When you show a number using the Fewest Pieces Rule, how do you know what number is shown? (The pieces tell me how many hundreds, how many tens, and how many ones are in the number because there are no more trades to make.)

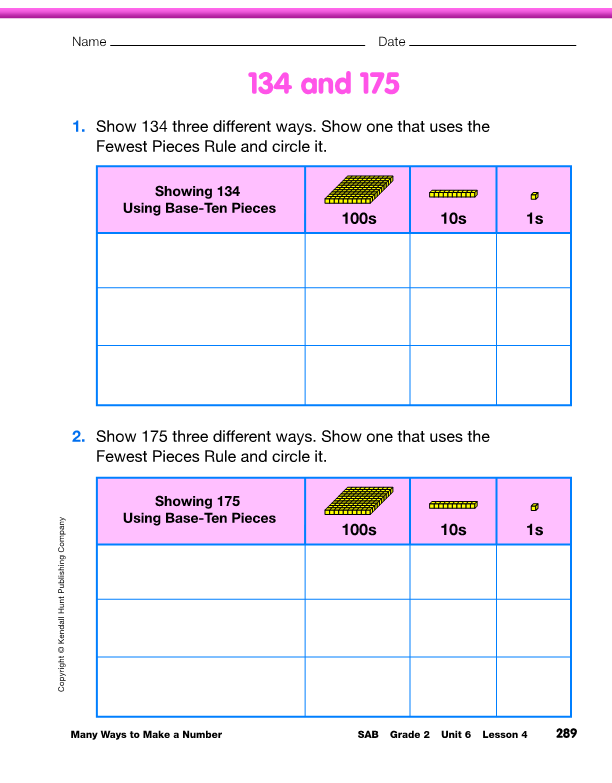
Represent 134 and 175. Have students complete the 134 and 175 page in the Student Activity Book in pairs. When they have completed the page, have them discuss their representations of the two numbers. See the Sample Dialog.

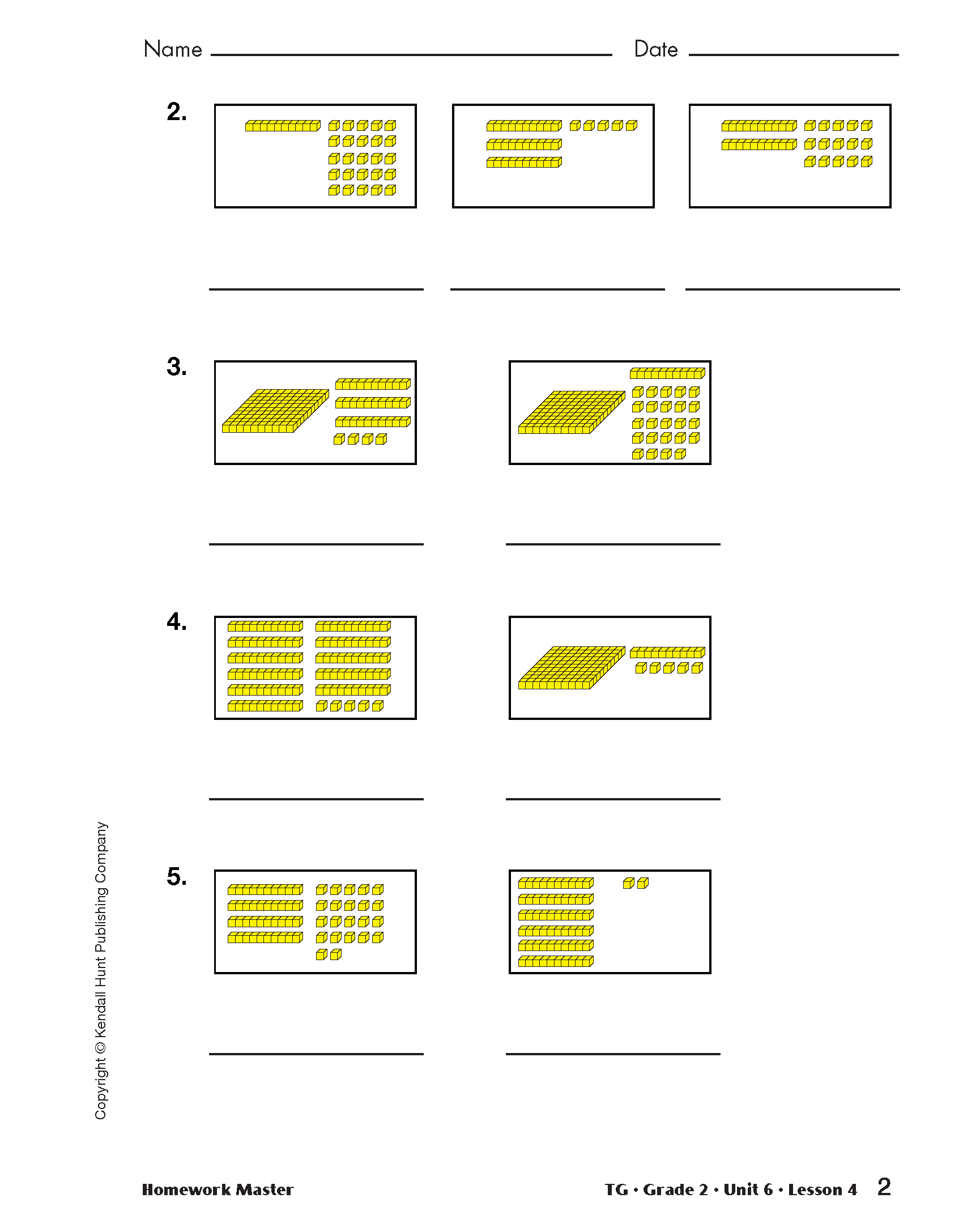
Assign the Base-Ten Pieces and Numbers Homework Masters.

X

Use this sample dialog to lead a discussion of the Fewest Pieces Rule with the 134 and 175 page in the Student Activity Book.

Teacher: How did you represent 134 on your Base-Ten Recording Sheet?

Maria: I used 13 skinnies and 4 bits.

Teacher: Who can record Maria's representation using base-ten shorthand on the recording sheet on the display? Maria, tell Keenya what you recorded.

Maria: You need to draw 13 sticks and 4 dots.

Teacher: Let's fill in the chart. How many flats should Keenya record? How many skinnies should she record? How many bits should she record?

Students: 13 skinnies and 4 bits.

Teacher: Did someone represent 134 a different way?

Josh: I had one flat, 3 skinnies, and 4 bits.

Teacher: Who can draw Josh's representation on the recording sheet? Josh, help David show your way.

Josh: Draw 1 square, 3 sticks, and 4 dots.

Teacher: How many flats, skinnies, and bits is that?

Josh: One flat, 3 skinnies, and 4 bits.

Teacher: Who can tell us another way to show 134?

Jackie: I did one flat, 2 skinnies, and 14 bits.

Teacher: Jackie, can you come draw your representation on the display?

[Jackie draws her representation and fills in the recording sheet.]

Teacher: Which one of these three representations uses the Fewest Pieces Rule?

Nila: The second one, Josh's, because he used a lot less pieces.

Teacher: Which one tells us the number?

Nila: Josh's tells the number. It has one hundred, 3 tens, and 4 ones, so it's 1–3–4,134.

Adventure Book:
Student Activity Book: 287 288 289
Answers
X
SAB_Mini
+
X
SAB_Mini
+
X
SAB_Mini
+
Master: BTP1 BTP2
Answers
X
SG_Mini
+
X
SG_Mini
+
Sample Base-Ten Recording Sheet showing different ways to partition 200, 140, and 50
X
+