Compare Numbers with Base-Ten
Pieces. Ask student pairs to display 37 and 73 with base-ten
pieces using the Fewest Pieces Rule.
- How do we know which number is greater? Are
there any clues that we get from the base-ten pieces? (Possible
response: Seven skinnies [tens] is more than 3 skinnies
[tens]. So, 73 is greater than 37.)
- What about the bits? Isn't 7 bits more than 3
bits? (But the 7 bits goes with 3 skinnies, and the 3 bits
goes with 7 skinnies. 70 is more than 30.)
- Can we count the number of pieces to know which is
greater? Why or why not? (No; They both have the
same number of pieces—10.)
- Are both of these numbers represented with the
Fewest Pieces Rule? That is, can I make any trades for more
skinnies? (All possible trades have been made.)

In discussing these and other examples, discussion points
that should be addressed are:
- Each representation uses the Fewest Pieces Rule.
- The total number of base-ten pieces does not determine
which number is greater.
- Use the names of the pieces and the place value of the
digits interchangeably. For example, a student may say, "I saw
that there were 2 flats in both numbers. One number had 5
skinnies and the other number had only 3, so I knew the one
with 5 skinnies was larger." You can respond, "So you knew that
the hundreds were the same and that 5 tens was more than 3
tens."
- When comparing numbers, encourage students to think of
the size of the pieces that represent the numbers so that they
create visual images of the numbers.
- If in 2 three-digit numbers, one number has more flats
than the other number, the one with the most flats is the
greater number.
- If in 2 three-digit numbers, the number of flats is the
same, the one that has the most skinnies will be the greater
number.
- If in 2 three-digit numbers, the number of flats and
skinnies is the same, the one with the most bits will be the
greater number.
A number sentence to show that 73 is greater than 37 can be
written as 73 > 37, read as 73 is greater than 37. The number
sentence can also be written as 37 < 73, read as 37 is less than
73. Note that in both cases, the opening of the arrow is on the
side of the greater number. Also, the arrow points to the smaller
number.
- Write a number sentence comparing 73 and 37
using the < , >, or = symbols. (37 < 73 or 73 > 37)
Pose a few more examples in which students compare two
2-digit numbers using base-ten pieces, then write and read a
number sentence using <, >, or =.
For each of the following pairs of three-digit numbers, ask
students to represent the numbers with base-ten pieces using the
Fewest Pieces Rule. Then ask them to decide which number is
larger and to write a number sentence using < or > to compare the
numbers. Possible responses are given.
- 105 and 123 (105 < 123)
- 313 and 245 (313 > 245)
- 212 and 219 (212 < 219)
- 199 and 207 (199 < 207)
For each set of numbers, ask questions similar to those
asked when comparing 73 and 37. Using the base-ten pieces will help students develop
mental images of the size of the numbers. Encourage students to
consider the size of the pieces that represent each number. For
example, when comparing 105 to 123, both numbers have one flat
(hundred), so students will need to compare the number of the
next largest piece, the skinnies (tens).
- Display 1 flat, 3 skinnies, 15 bits, and 1
flat, 4 skinnies, 5 bits.
In this example, the numbers are the same, but their
representations are different.
Ask students to work with a partner to answer the
following questions:
- Which set of base-ten pieces do you think
represents the larger number? Why?
- How can you find out?
Students may realize that since the number of flats
(hundreds) is the same that they need only compare the remaining
pieces. If they make trades until they represent the number using
the Fewest Pieces Rule, they will see that the two sets of pieces
represent the same number. Other strategies are possible.
- Is this a true statement: 100 + 30 + 15 = 100 + 40 + 5? Explain how you know.
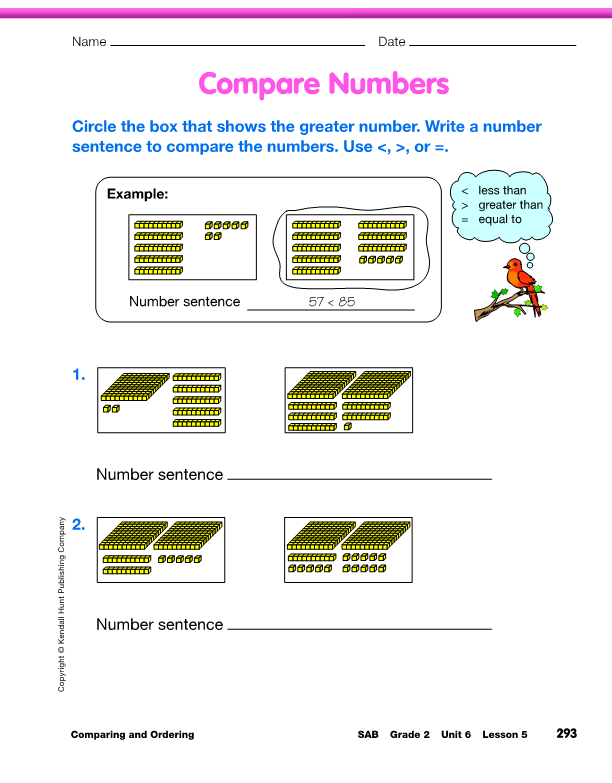
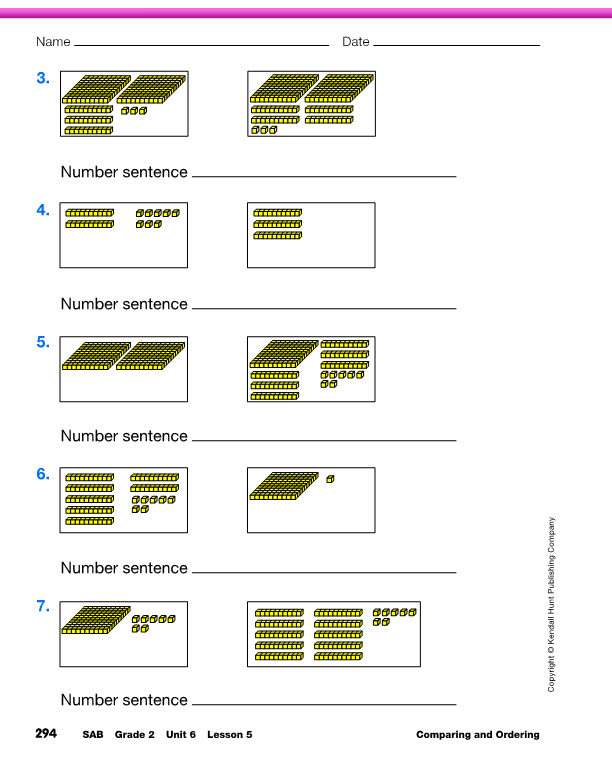
Assign the Compare Numbers pages in the Student
Activity Book. Students circle the number that is greater and
write a number sentence. If the numbers are equal, they should
not circle any of the numbers.
Order Numbers with Base-Ten
Pieces. Ask student pairs to show 54, 81, and 45 using base-ten
pieces.
Ask them to display them in order, from smallest to
greatest.
- How do you know which number is greatest? How
do you know which number is smallest? Are there any clues
that we get from the base-ten pieces? (The skinnies are the
larger piece, so the bits won't matter if you can't make any
more trades. So 45 is smallest because it has the fewest
skinnies, 81 is the greatest, and 54 is in the middle.)
- Did you notice that all the numbers have the
same number of base-ten pieces? Does the number of base-ten
pieces matter when we want to find the smallest or largest
number? (No, the number of base-ten pieces is not important.)
- Write 54, 81, and 45 in order from smallest to
largest. (45, 54, 81)
Ask student pairs to show 131, 122, and 113 using base-ten
pieces. Ask them to display them in order, from smallest to
largest. Each of these numbers is represented by the same number
of base-ten pieces. Each representation has one flat. The number
of skinnies that each number has determines its place in the
ordering.
Ask students to write 131, 122, and 113 in order from
smallest to largest (113, 122, 131).
Ask students to display 221, 122 and 131. Ask them to
display them in order, from smallest to greatest. Each of these
numbers can be represented by the same number of base-ten pieces
using the Fewest Pieces Rule. In this example, one number has
more flats than the other two numbers. That number would be the
greatest. The other two numbers each have one flat. These numbers
need to be compared by their skinnies.
Ask students to write 221, 122, and 131 in order from
smallest to largest (122, 131, 221).
Place Numbers on the Number
Lines.
Ask students to compare 103 and 130 with base-ten
pieces.
- Which is the greater number? How do you know?
(130 is greater than 103. They have the same number of flats,
but 130 has 3 skinnies and 103 has none.)
- Write a number sentence comparing 130 to 103.
(130 > 103)
- Look at the 103 and 130 on the number line. Describe their positions on the number line.
(103 goes before 130; 103 is closest to 100, 130 is farther from 100.)
Ask students to compare 57, 99, and 75 with
base-ten pieces.
- Which is the greatest number? How do you know?
(99 is greatest. It has the most skinnies.)
- Which is the smallest number? How do you know? (57
is the smallest number. It only has 5 skinnies.)
- Look at the numbers on the number line.
Describe their positions on the number line. (57 goes first,
then comes 75, and then comes 99.)
Draw a number line on chart paper or the board with the
friendly numbers or benchmarks of 0, 50, and 100. Use base-ten
shorthand to show each benchmark with base-ten pieces. See
Figure 1. Ask students to help you place the numbers 57, 99, and
75 on the number line.
- What number would you like to place first?
- Where should I put 57, before the 50 or after
the 50? How do you know? (57 goes after 50. I looked at the
class number line.)
- Is 57 closer to 50 or closer to 100? How do you
know? (57 is closer to 50. It is closer on the class number
line.)
- Is 57 closer to 50 or closer to 60? How do you
know? (57 is closer to 60. 57 is only 3 away from 60 but 7
away from 50.)
Move your finger or pointer to different places on the
number line. Ask students to raise their hands when they think
you are near where 57 should be. When most students have their
hands up, write a mark for 57 on the number line and write 57
under the number line.
- Where should I put 99, before 50 or after 50?
How do you know? (After 50. 99 is definitely larger than 50.)
- Is 99 closer to 50 or closer to 100? How do you
know? (99 is closer to 100. It is one smaller than 100.)
Move your finger back and forth on the number line. Ask
students to raise their hands when they think you are near where
99 should be. When most students have their hands up, write a
mark for 99 on the number line and write 99 under the number
line.
- Now we have to place 75 on the number line.
Where should I put it, before the 50 or after the 50? How do
you know? (75 goes after 50. I looked at the class number
line or 200 Chart.)
- Is 75 closer to 50 or closer to100? (75 is
between 50 and 100 like 75¢ is between 50¢ and 100¢.)
Move your finger or pointer to different places on the
line. Ask students to raise their hands when they think you are
near where 75 should be. When most students have their hands up,
write a mark for 75 on the number line and write 75 under the number line.
Repeat the above for more numbers. Examples are 15, 39, and
92; 23, 73, and 89; 29, 67, and 88. Draw more number lines as
shown in Figure 1.
Draw a new number line as shown in Figure 2. The friendly
numbers or benchmark numbers on this line are 0, 50, 100, 150,
and 200.
Ask students to help you place the numbers 27, 130, and 185
on the number line. Use the same questions and routine you used
previously.
- Where should I place 185? Is it closer to 100
or 200? (185 is closer to 200.)
- Where should I place 130? What two numbers is
it in between? Which is it closer to? (130 is between 100 and
150 but closer to 150.)
- Where does the 27 go? (27 is more than 0 but
less than 50. It is in the middle.)
- Which number is the largest? (185)
- Which number is the smallest? (27)
Ask students to complete the Walk the Number Line pages
in the Student Activity Book.
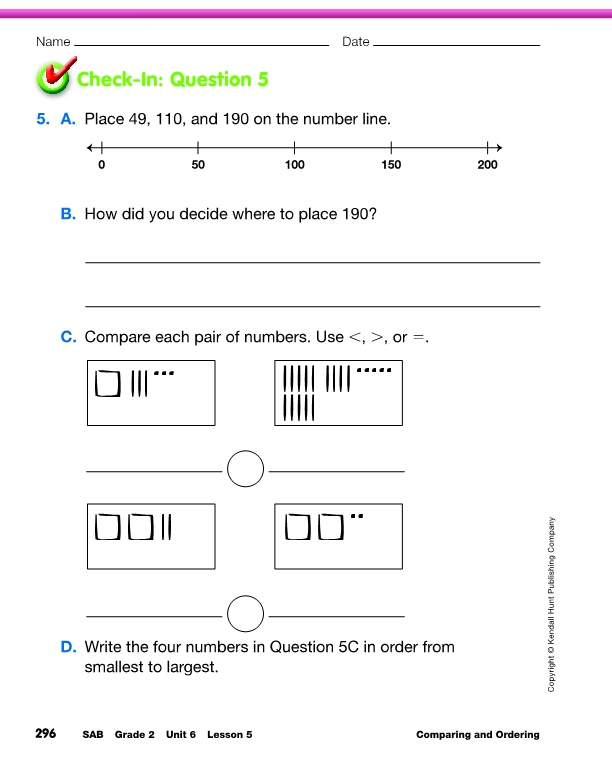
Use Check-In: Question 5 on the Walk
the Number Line pages in the Student Activity Book to
assess students' abilities to compare and order numbers using
base-ten pieces and a number line [E8]; use words and symbols to
show comparisons of quantities [E7]; estimate a quantity using
benchmarks [E6]; and show their thinking [MPE5].
The Workshop in Lesson 7 provides targeted practice with
these Expectations.