Base-Ten Hoppers Again

Est. Class Sessions: 1

Developing the Lesson

One of the goals of the lesson is to help students develop flexibility with numbers. Students have opportunities to express numbers in different ways on the number line, with base-ten pieces, and by writing number sentences. Although the base-ten hopper only makes hops of ones, tens, and hundreds, students should feel free to write, or say, a 30 for 3 tens in a number sentence, or to write 30 over 3 hops of ten. See Figures 1 and 2.

Review Base-Ten Hoppers.

Hold up a bit, a skinny, and a flat, one at a time. With each piece ask:

If a base-ten hopper goes this far, how far does it hop?

Review with students what a base-ten hopper can and cannot do on a number line. Make a list on a display.

Some points students might make:

The base-ten hopper can only jump by base-ten pieces such as ones, tens, and hundreds.
The base-ten hopper can move forward and backward.
The base-ten hopper can start and stop at any number on the number line.
The number above each hop tells how far the base-ten hopper moved.
If the hop has a plus (+) sign, the base-ten hopper moved forward.
If the hop has a minus (–) sign, the base-ten hopper moved backward.

Show a display of the Open Number Lines Master.

Hold up the bit, skinny, and flat all together and ask:

What number am I showing? (111)
How can the base-ten hopper hop on the number line to reach this number? Who can show me? (100 + 10 + 1)
[Student name] showed the hops by starting with the flat. Who can show me a different way? (Possible response: 1 + 10 + 100)

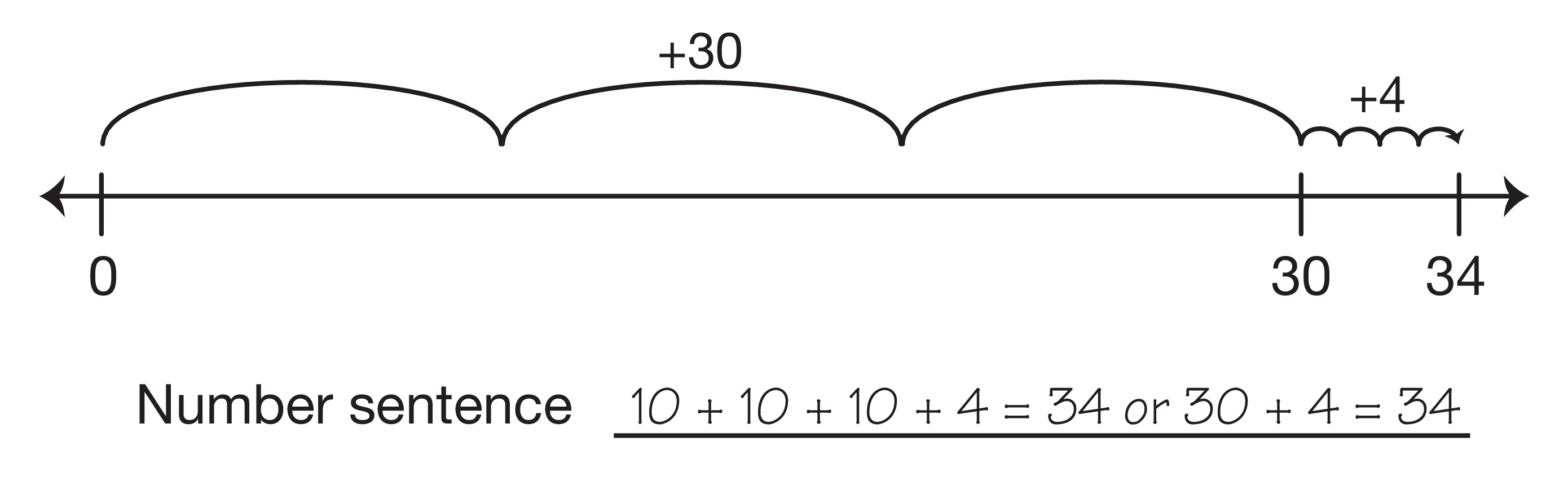
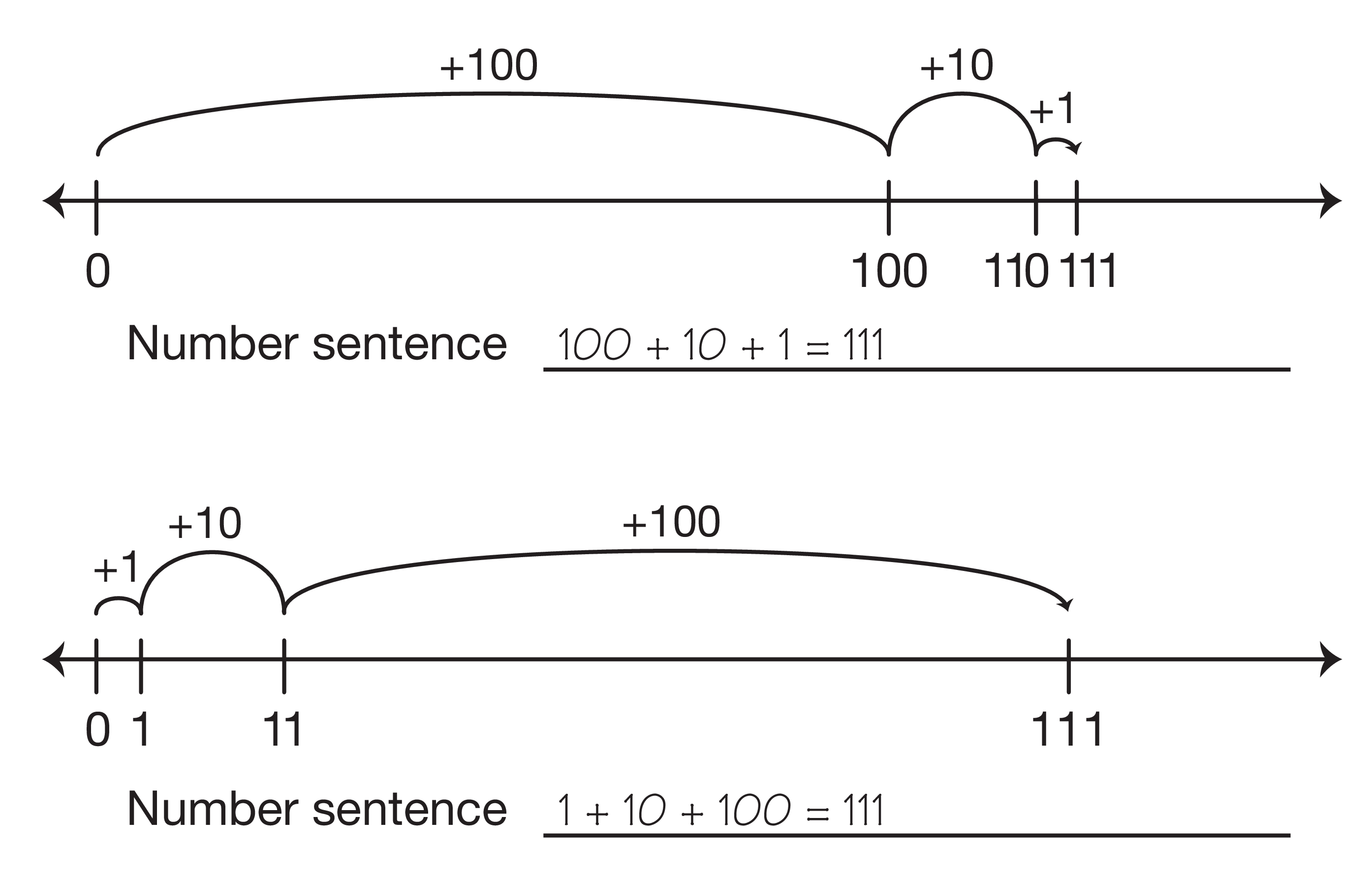
Have students draw the hops starting with different pieces. For example, if the first student draws hops starting with the flat (100 to 110 to 111), ask another student to show the hops starting with the bit, (1 to 11 to 111). See Figure 3. Leave both representations on display and ask students to tell you a number sentence to match each representation.

Hold up the same pieces as before and add another skinny. Ask students what number is represented. Have them draw the base-ten hopper's hops to reach the number (121). Ask a student to draw the hops; then have another student draw it a different way.

Compare Moves on the 200 Chart and Number Line. Leave both representations up and ask students to write number sentences. Ask students to show the same number sentences on a display of the 200 Chart. For example,
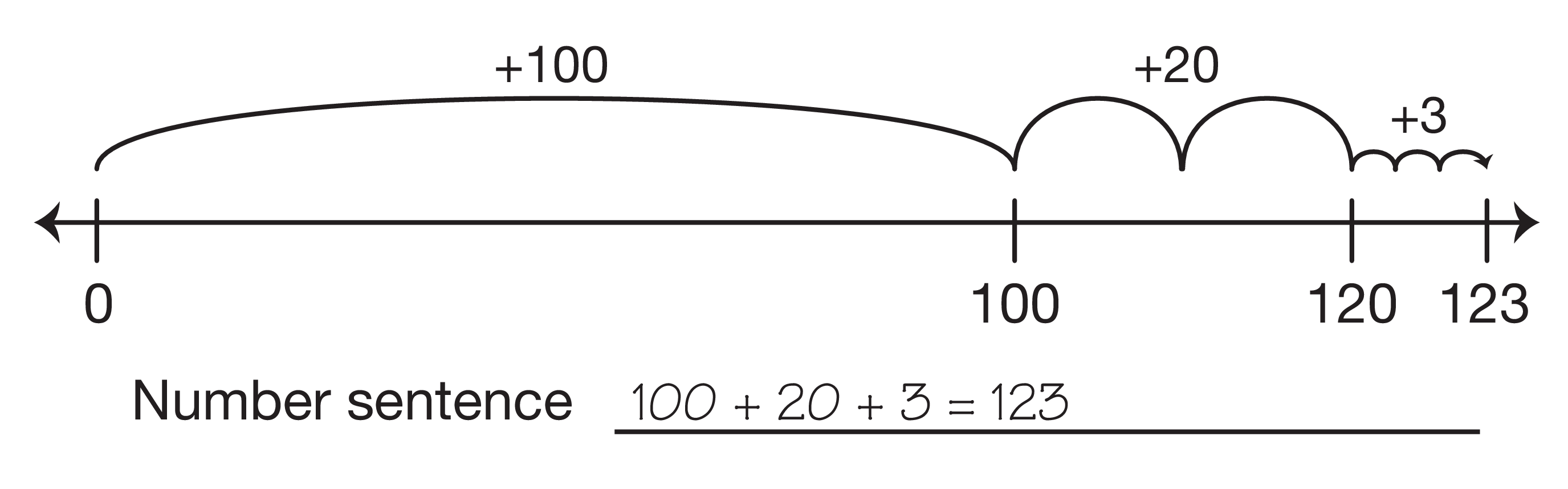
100 + 10 + 10 + 1 = 121 is one move from zero to 100, then moving down two rows to 110 and 120, then to the right 1 space, 121. A number sentence that matches starting with the bits (1 + 10 + 10 + 100 = 121) would be shown on the 200 Chart by moving from zero to 1, then down two rows to 11 and 21, then down 100 or ten rows to 121. As students make each move on the 200 Chart, ask them how it is like the number line or the base-ten pieces.

Show students a few more small collections of base-ten pieces and ask them to show the number on the number line with hops of the base-ten hopper. Have them show the hops different ways, that is starting with different pieces, to get to the same number. Ask students to tell you a number sentence for each representation.

If you show 99 (or 109) with base-ten pieces, some students may choose to show 99 on the number line as one long hop (100) forward and one small hop (1) backward (or 109 as a hop of 100, a hop of 10 forward and a hop of one backward). This can lead to a productive class discussion. Discuss the number sentence that matches and the advantages and disadvantages of each representation.

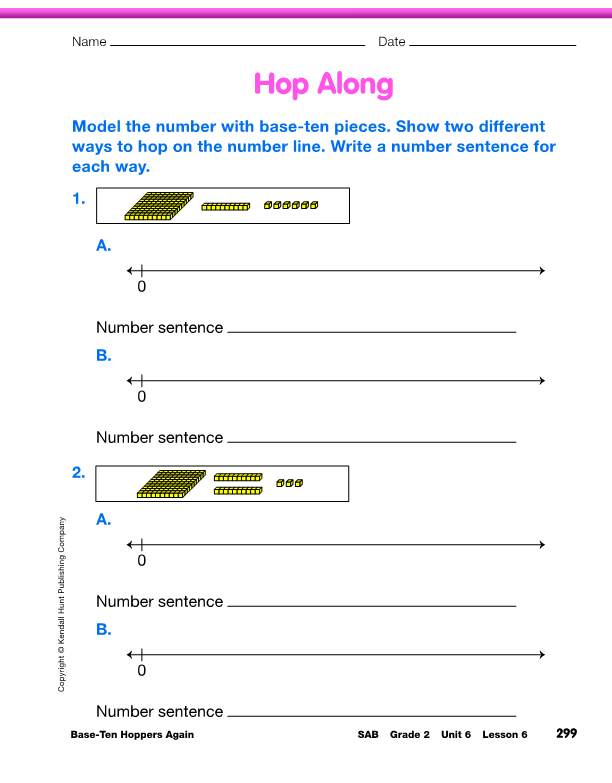
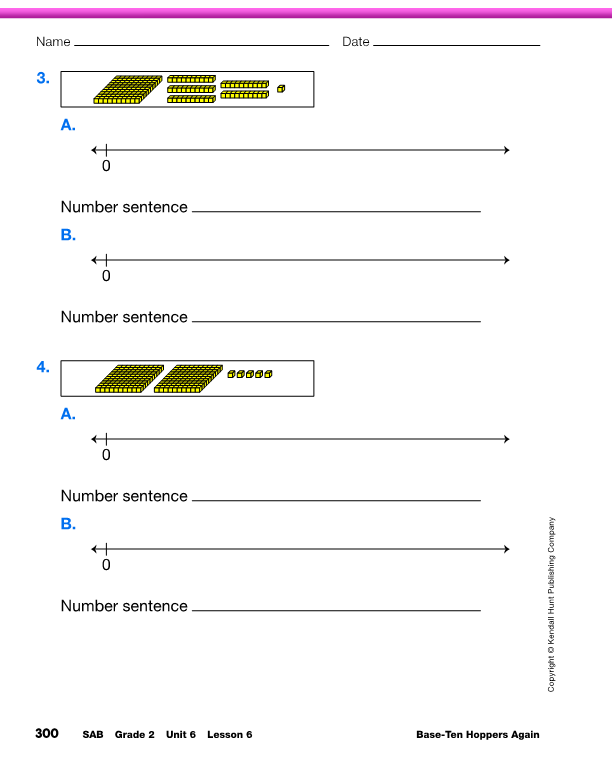
Connect Base-Ten Pieces to Hoppers and Number Sentences. Display and direct students to the Hop Along pages in the Student Activity Book. A number expressed in base-ten pieces is given. Students are asked to model the number with base-ten pieces, then show the number on the number line with hops of one, ten, and one hundred. They write number sentences to reflect their work.

Do the first problem with the class as a whole. The first picture shows one flat, one skinny, and 6 bits. One possible representation on the number line, starting with the flat, is to move forward with hops of one hundred, one ten, and six ones. A number sentence that matches is 100 + 10 + 6 = 116. If a student starts with the bits first, the hops are in reverse order and the addends in the number sentence are reversed. See the sample dialog for a discussion of Question 1. Ask students to work with a partner to complete the Hop Along pages.

Use this dialog as a guide to discussion of Question 1 on the Hop Along pages in the Student Activity Book.

Teacher: Is there another way the base-ten hopper can represent these blocks?

Irma: It could start with the skinny.

Teacher: Jerome, Irma says the base-ten hopper could start with the skinny. Can you show us the hops it would make?

Jerome: It would go to 10, then a big 100-hop, then 6 little one-hops. [Jerome draws the hops on the display and labels each hop correctly.]

Teacher: Nicely done, Jerome. Leah, what number sentence matches what Jerome has drawn?

Leah: 10 + 100 + 6 = 116. But he didn't have to do it that way. He could have done the 10-hop and then the 6 little one-hops next. Then his last hop would be the big 100-hop.

Teacher: Jerome, what do you think about what Leah said? Do you agree with her?

Jerome: I think so. I guess I could have done it that way.

Teacher: What is different about the way Leah said from the way Jerome said?

Roberto: Nothing. They both end at 116. It's just that Leah put the one-hops after the ten and Jerome put the 100-hop after the ten. But I think they are both right.

Teacher: What are the two number sentences, Roberto? Can you write them for us?

[Roberto writes 10 + 100 + 6 = 116 and 10 + 6 + 100 = 116.]

Teacher: How can you tell for sure if they are both right?

Roberto: The hops are the same—just in a different order—and it ends in the same place both times.

Upon completion, discuss how the different
representations—base-ten pieces, number line, and number sentence—are alike and different.

Ask students to reflect on their work and ask open-ended questions such as:

How are base-ten pieces, the hops on the number line, and the 200 Chart alike or different? For example, how is showing 100 each way alike or different? (Possible responses: They all show the same number. When you show 100 using the number line, it is one long hop. On the 200 Chart it is 10 rows. The flat is more like the 200 Chart because it is 10 rows of 10.)
How is showing 123 using base-ten pieces, hops on a number line, and on a 200 Chart alike or different? (Possible responses: They all have the same number sentences. You can show your moves in different orders with all three ways. For 123 on the 200 Chart, you show moves on the rows. Each row is like a skinny. When you show the 100 on the number line, it is in a long line.)
Which representation is most helpful to you? Why? Who agrees? Who doesn't agree? Why?
Which representation does not help you very much? Why?
When do you think it might be most helpful for you to use the base-ten pieces? The number line? A number sentence?
What about the 200 Chart? When do you think it might be most helpful to use the 200 Chart?

Adventure Book:

Student Activity Book: 299 300

Answers

Master:

Hopping 3 tens and 4 ones on the number line and writing a number sentence

Hopping 1 hundred, 2 tens, and 3 ones on the number line

Showing hops by the base-ten hopper to 111 two different ways

Unit 6

Unit Overview

Daily Practice and Problems

Lesson 1

Lesson 2

Lesson 3

Lesson 4

Lesson 5

Lesson 6

Lesson 7

Lesson 6

Base-Ten Hoppers Again

Developing the Lesson