From the Fish Hatchery

Est. Class Sessions: 2

Developing the Lesson

Part 2: Using Rectangles

Model Counting Squares. Display Question 1 on the first page of the Counting Squares pages in the Student Activity Book. Direct students to find the number of small squares in the rectangle for Question 1.

Ask:

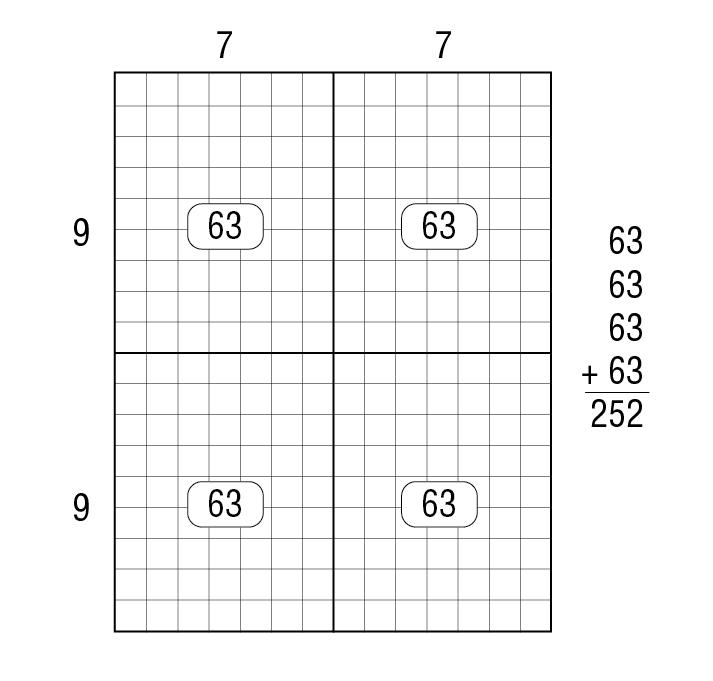
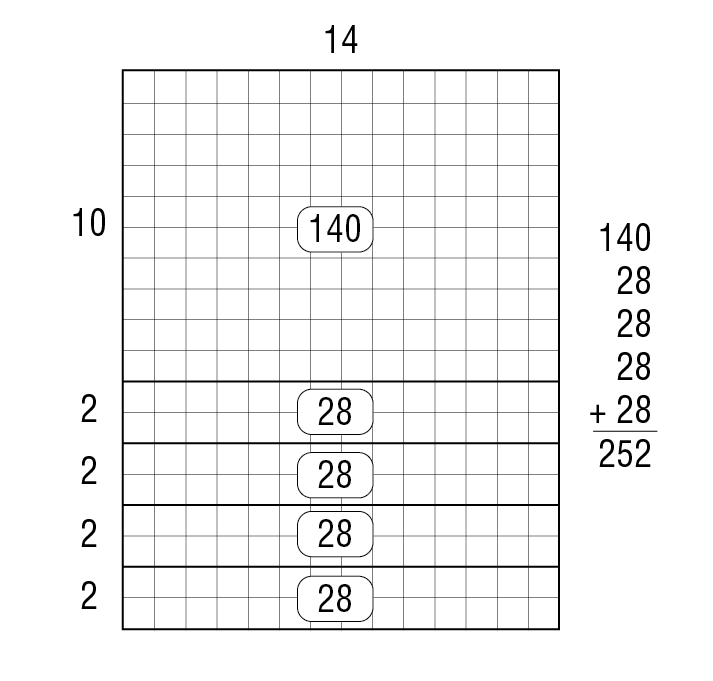
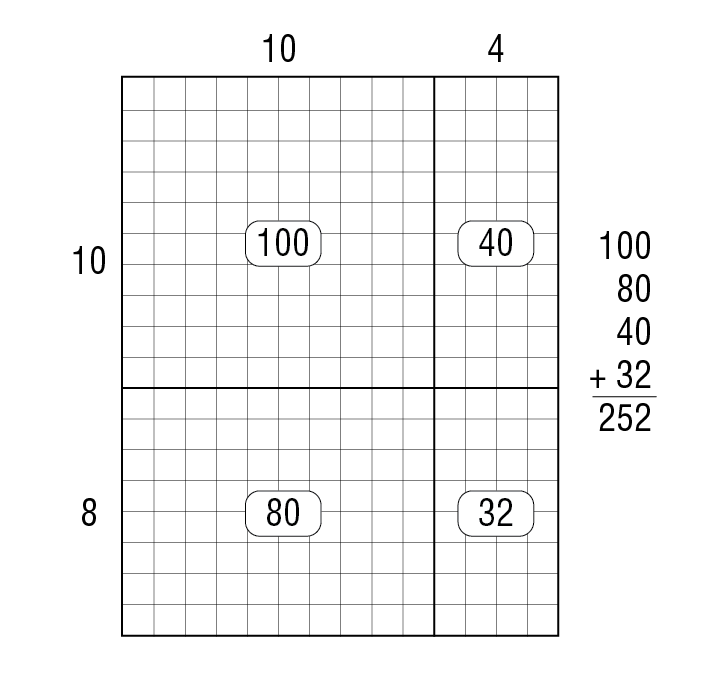
What multiplication problem does this rectangle represent? (18 × 14)
How do you know? (There are 18 rows and 14 columns.)

Allow students several minutes to solve the problem. Remind them to show their method. Pay attention to the strategies students use. Ask them to share how they figured the total number of squares in the rectangles. Make sure you include a student who solved the problem by partitioning the large rectangle into more manageable parts. Sample student responses for Question 1 are shown in Figures 3, 4, and 5.

Ask questions such as:

Who solved the problem by breaking the large rectangle into parts?
What parts did you divide your large rectangle into?.
Why did you choose those partitions? What were you thinking about?
How is your strategy different from [student name]'s strategy?
How is your strategy the same?
What did you multiply to get the numbers inside the rectangles?
How do the numbers inside the rectangles match the numbers in the addition problem?
Which partitions are easier to work with to solve the problem? Why?

If students do not offer the solution in Figure 5, ask:

How can you divide the rectangle using place value, that is, using tens and ones?

Ask a student to show how to divide the rectangle into tens and ones on a class display of the first Counting Squares page. Then explain the partial products.

Explore Ways to Count Squares. Ask students to complete Question 2 on the Counting Squares pages using a different method for dividing up the rectangle from the one they used for the previous problem. If students are having difficulty thinking of new methods on their own, suggest that they try one of the methods that was shared for the previous problem. After giving students several minutes to solve the problem, ask them to explain to a partner how they solved the problem. Then ask two or three students to explain their strategies to the class. Continue recording students' methods on a class display of Counting Squares Question 2 as different methods come up. Sample solutions that use place value are shown in Figure 6. Ask a student to show the class how to divide this rectangle into tens and ones.

Ask:

What do you multiply to get these partial products? Show me where they are on the rectangle. (Possible response using the first example in Figure 6: 10 × 10 = 100 twice, 10 × 3 = 30, 8 × 10 = 80 twice, and 8 × 3 = 24)
Are these partial products easy to multiply? Easy to add together?
What is another way to break apart 23 using tens and ones? (23 = 20 + 3)
What does the rectangle look like then? (See the second example in Figure 6. Ask a student to divide the rectangle this way.)
What do you multiply to get these partial products? Show me where they are on rectangle. (10 × 20 = 200, 10 × 3 = 30, 8 × 20 = 160, 8 × 3 = 24)
Are these partial products easy to multiply? Easy to add together?
Which of the strategies has fewer partial products to add together? (Using 23 = 20 + 3)

Using Rectangles. The vignette in the Using Rectangles section of the Student Guide begins the discussion of solving multidigit problems using paper-and-pencil methods.

A new multiplication problem is presented:

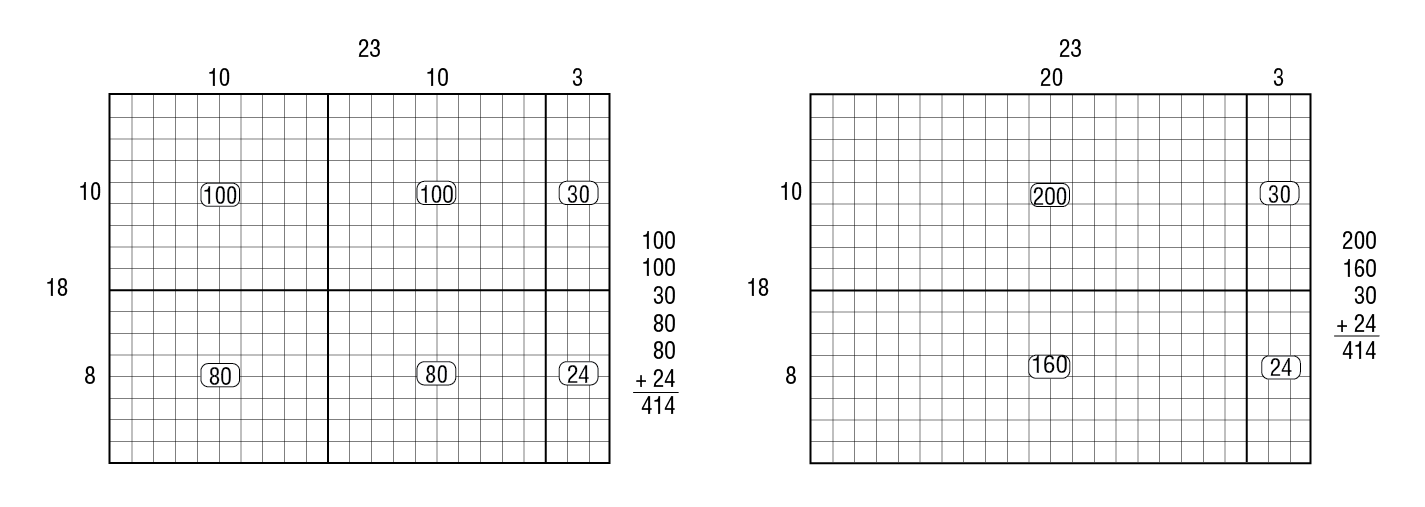
How much water is in 13 containers with 24 ounces of water each?

Discuss the two rectangles drawn by Grace.

Ask:

How did Grace break apart 13 and 24? (Grace divided 13 into 10 and 3. She divided 24 into 20 and 4.)
Where did the number sentences in each part come from? (Possible response: Grace found the area of each part by multiplying.)
Looking at the rectangle with the grid, are the number sentences correct? How do you know? (Possible response: Yes, I used what I learned to multiply multiples of 10.)
How do the number sentences in the rectangle parts relate to the addition problems written outside the rectangles? (Possible response: The addition sentence adds up all the answers to the multiplication sentences.)
How are Grace's two rectangles the same? (The rectangles both divide 24 and 13 into tens and ones.)
How are they different? (One rectangle shows all the squares. The other one can be drawn without grid paper and is quicker, but it is not drawn exactly to scale.)

When students are familiar with using rectangles to show break-apart products with tens and ones, have them work in pairs or small groups to answer Question 6 and discuss the vignette that follows in the Student Guide.

Ask pairs to work on Questions 7 and 8. Question 8 leads students to consider a method of estimation that flows from the rectangular array model. Students may respond that an estimate of 200 is not very close when the actual answer is 312. This model presents a visual demonstration of why the estimate is low (much of the product comes from the other three partial products).

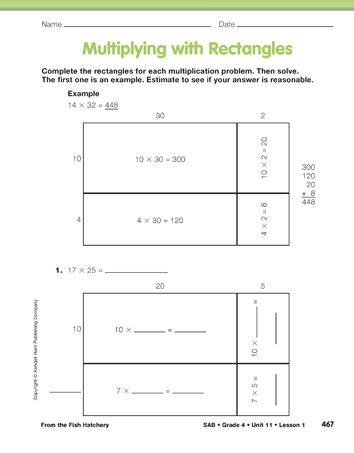
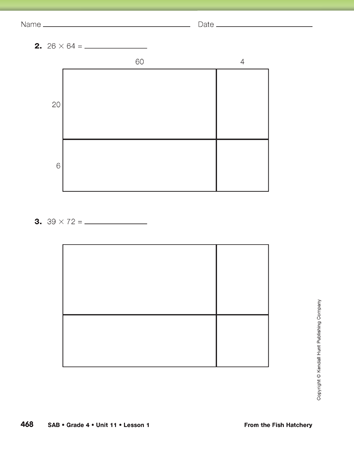
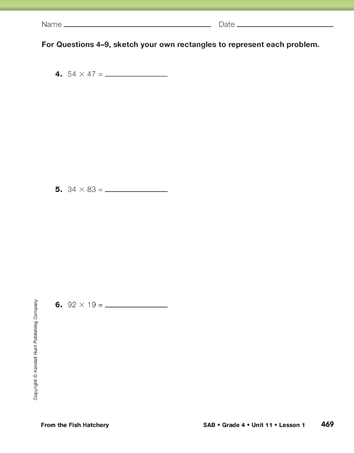
Ask students to complete the Multiplying with Rectangles pages in the Student Activity Book. As they solve the problems, have them compare partial products and answers with others in their small groups. Circulate as they work to see if students are able to extend their understanding of the rectangle model to 2-digit by 2-digit problems.

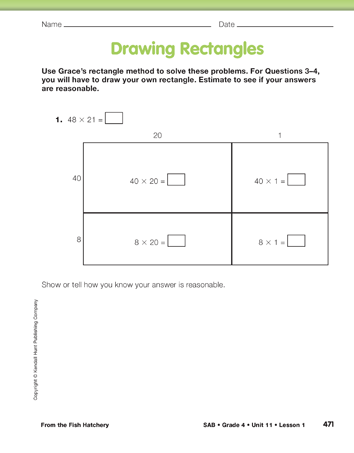
At this point, you may assign the Drawing Rectangles pages in the Student Activity Book as homework. Unfinished problems from the Multiplying with Rectangles pages in the Student Activity Book may also be assigned as homework.

If students are having trouble sketching their own rectangle models on blank paper, provide them with a copy of the Half-Centimeter Grid Paper Master. The grid will support their ability to draw a useful model of the multiplication problem.

Student Guide: 489 490

Answers