Estimate First. Have students read the opening vignette in the All-Partials Revisited pages in the Student Guide. Ask students to share their estimates and their strategies for Question 1. Remind students to choose numbers that are easy for them to multiply in their heads.
Display a few of the suggested estimation strategies. A few are listed here, but your students may have others:
- Round 24 to 20 and multiply: 20 × 28 = 560.
- Round 24 to 20 and round 28 to 30 and multiply: 20 × 30 = 600.
- Round 24 to 25 and round 28 to 30 and multiply: 25 × 30 = 750.
- Round 24 to 25, multiply 28 × 100 and divide by 4: 2800 ÷ 4 = 700.
Ask students to discuss the following with a partner:
- Which of the estimates on the board do you think are higher than the exact answer? Which are lower? Why? (Possible response: 560 will be lower than the exact answer because 20 is less than 24. 750 will be higher than the exact answer because both numbers are rounded up.)
- Which estimate do you think is closest? Why? (Possible response: 700 may be closer because 25 is only one more than 24.)
Students should note that when one number is rounded up and the other is rounded down, it is more difficult to tell whether the estimate is going to be higher or lower than the exact answer. Have students compare their estimates with Ana's exact answer in the vignette.
Use Three Methods. For Question 2, have student pairs take turns explaining the partial products to one another.
- How did Ana get the partial product 32? How did she know it was 32 and not 320? (Ana multiplied 4 × 8. Both digits are in the ones place.)
- How did Ana know to multiply 4 × 20 and not 4 × 2? (Possible response: The 2 is in the tens place in 28, so you have to multiply 4 × 2 tens and that is 4 × 20, or 80.)
- Why did Ana multiply 20 × 8 next? Where did the 20 come from? (She broke 28 apart into 20 and 8.)
- How did Ana get the partial product 20 × 20? Why didn't she multiply 2 × 2 or 2 × 20? (Possible response: Ana multiplied the 20 in 24 times the 20 in 28.)
Students compare using the rectangle method, expanded form, and all-partials method to solve a 2-digit by 2-digit multiplication problem. Have students describe the similarities and differences for Question 3.
- What is the same about all-partials, the rectangle model, and expanded form? (Both numbers being multiplied are broken into tens and ones. The partial products are the same in all three methods. They come from multiplying the ones in 24 times the ones in 28 (4 × 8), the 4 ones in 24 times the 2 tens in 28 (4 × 20), the 2 tens in 24 times the 8 ones in 28 (20 × 8), and the 2 tens times the 2 tens (20 × 20). All the partial products are added together.)
- What is different? (In the all-partials method, the numbers are mentally broken into tens and ones, but the partitions are not put in writing.)
Question 4 addresses the idea that the order of the partial products does not make a difference in reaching a correct answer.
Practice Methods for 2-Digit by 2-Digit Multiplication. Have students complete Questions 5–10. The problems provide practice for the all-partials method, expanded form method, and rectangle model of multiplication.
Circulate and ask individual students questions such as:
- Show me the partial products.
- What two numbers did you multiply to get this product?
Question 10 is an opportunity to remind students that an estimate can help them prevent errors in their exact answers. A quick mental estimate of 50 × 50 = 2500 should tell students that Roberto's answer of 329 is much too low and he needs to find and correct his mistakes.
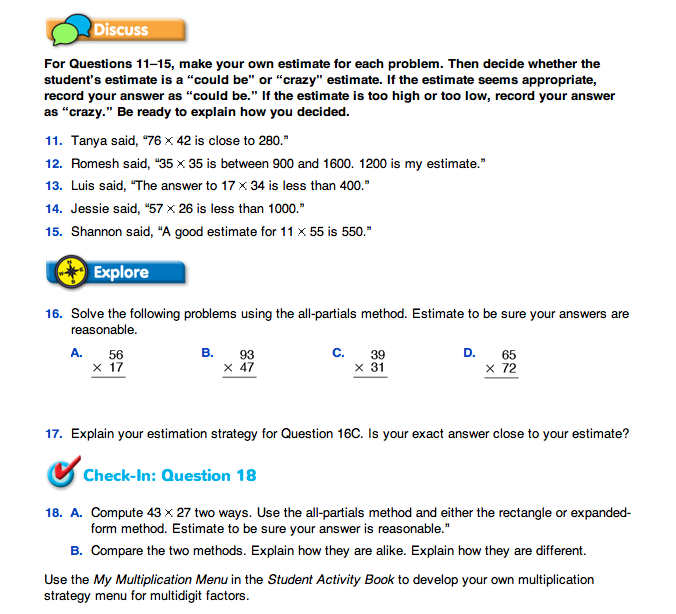
Check Estimates. Have students work in small groups to evaluate the estimates in Questions 11–15. Have different groups present their answers for the different problems. Encourage other groups to ask the presenting group questions.
Ask questions like the following:
- How do you think [student name] came up with that estimate?
- What “friendly” numbers do you think he or she used?
- Is this a “could be” or “crazy” estimate?
- Did you find a different estimate?
- How did you find your estimate?
- What “friendly” numbers did you use?
Have students practice using the all-partials method and estimating to see if their answers are reasonable using Questions 16 and 17.
Compare Methods. Ask students to read Question 18 with a partner and discuss how they can meet Math Practices Expectations 1, 3, and 5 on the Math Practices page in the Reference section of the Student Guide.
As partners are discussing their responses, ask:
- How will you show that you know what the problem is asking (for Math Practices Expectation 1)? (Possible response: I will multiply 43 × 27 two ways—once using the all-partials method and once using either the rectangle model or expanded form.)
- How will you show that you checked for reasonableness (for Math Practices Expectation 3)? (I will show my estimation strategy and then show if it is close to my exact answers.)
- How will you show your work (for Math Practices Expectation 5)? (I will show all my steps for both methods and I will show my estimation strategy. Then I will explain where the numbers in the all-partials method are in the other method and how I got them.)
Before students turn in their papers, ask them to trade with another student and use a copy of the All-Partials Revisited Check-In: Question 18 Feedback Box Master to give one another suggestions for improving their work. Students then revise their explanations based on their classmate's feedback.

Use Check-In: Question 18 in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' progress toward showing connections between models and strategies for multiplying 2-digit by 2-digit numbers [E2] and multiplying 2-digit by 2-digit numbers using mental math strategies and paper-and-pencil methods [E4].
Also use this question to assess students' abilities to communicate their solutions using the Math Practices Expectations below:
- MPE1. Know the problem. I read the problem carefully. I know the questions to answer and what information is important.
- MPE3. Check for reasonableness. I look back at my solution to see if my answer makes sense. If it does not, I try again.
- MPE5. Show my work. I show or tell how I arrived at my answer so someone else can understand my thinking.
The Workshop in Lesson 3 provides targeted practice with Expectations 2 and 4.