Choosing Strategies to Multiply

Introduce Dancing in TIMSville. Read with the class the extended, open-response problem on the Dancing in TIMSville pages in the Student Activity Book. After reading through the introduction and instructions, lead a discussion to help students understand the problem.

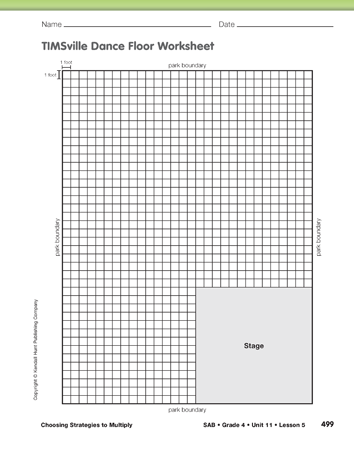
Display a copy of the TIMSville Dance Floor Worksheet to help students get a sense of the shape of the dance floor and the space in which it needs to fit. Draw several shapes and ask whether the shape meets the first three of the mayor's rules for the design. For example, show a dance floor that extends outside the park boundaries, that overlaps the stage, or that is made of a shape that cannot be covered by two rectangles.

Review Math Practices. Direct students' attention to the Math Practices page in the Reference section of the Student Guide. Tell students that for this problem they should concentrate on finding good tools and an efficient strategy [MPE2], looking back at their solutions to check for reasonableness [MPE3], and showing their work so that the mayor can understand their thinking [MPE5].

Remind students to use the worksheet to try different strategies and solutions. The mayor will not see this page. The final design, however, should show the solution clearly and accurately.

Solve the Problem. Students work in groups of three to four to solve the problem. This should provide each group with enough grid-paper worksheets to try several different strategies. Circulate as groups work on the problem.

If groups finish the problem quickly, challenge them to find other creative designs that fit the rules.