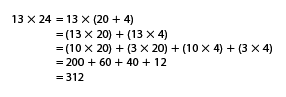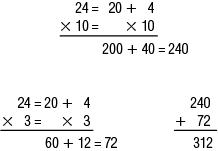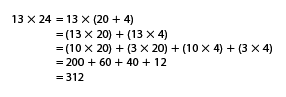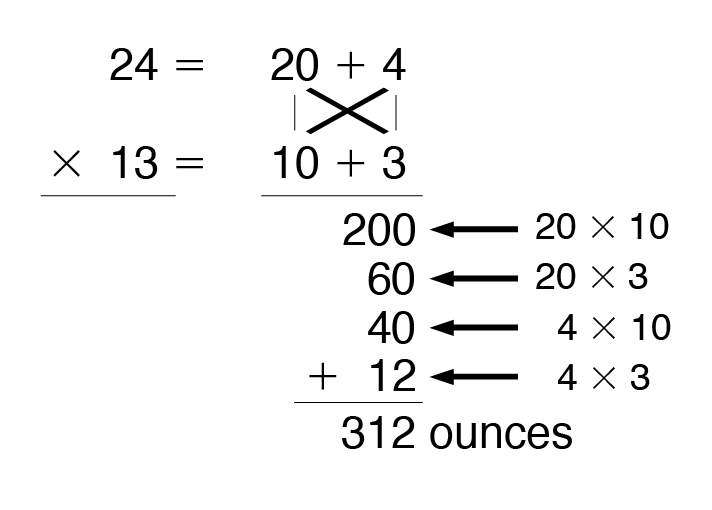Lesson 1

From the Fish Hatchery

Est. Class Sessions: 2

Developing the Lesson

Part 3: Connecting Rectangles to Expanded Form

The Expanded Form with 2-Digit Numbers section in the Student Guide reminds students of using the expanded form to solve multiplication problems. The conversation in the vignette and Questions 9–12 take students through the problem step by step and ask them to compare their work with Grace's rectangle models solving the same problem.

X

Expanded Form with 2-Digit Multipliers. Using the expanded form to solve multiplication problems with 2-digit multipliers is similar to using this method when solving problems with a single-digit multiplier. However, there are a few more steps and, therefore, greater risk of error. The expanded form is practiced in conjunction with the rectangular model and the all-partials method (covered in Lesson 2) so that students will get used to the idea that there is a partial product for each digit in t he multiplicand and in the multiplier. Consequently, they should more easily recognize when they have left out one of the steps. See Figure 7.

The diagrammatic depiction of the problem as shown in Figure 7 and in the Student Guide may at first appear confusing to students. Have students trace the lines with their fingers and then find the partial product below that is the product of the pair of digits linked by the line. For example, tracing the line that connects 20 and 3, the student finds the product (60) below the line. Ask several students to use the connecting lines in the diagram to demonstrate the steps of the problem on the board.

X

If students have trouble finding all the partial products as shown in Figure 7, ask them to break the problem into two problems as John shows in the Student Guide. So for 24 × 13, the problem is broken into 24 × 10 and 24 × 3.

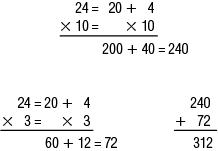
Students complete Questions 13–15 and compare their answers with a partner or with others in their small groups.

X

Using rectangles and expanded form supports students' understanding of multidigit multiplication. For students who are struggling, the rectangles provide a visual image of the partial products. Both methods provide a structure for decomposing the factors into tens and ones and keeping track of the partial products.

For advanced students, these methods provide a structure for using the distributive property that is used in algebra:

Student Guide: 491
Answers
X
SG_Mini
+
Student Activity Book:
Master:
Example of using expanded form to solve a multidigit multiplication problem
X
+