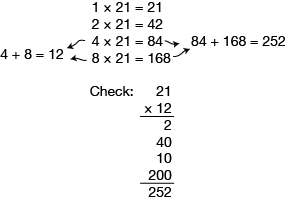Tell students that they will explore another multiplication strategy, one that comes from Ancient Egypt. Before students read the story in the Student Guide, help them pronounce unfamiliar vocabulary such as hieroglyphics, duplation, papyrus, and the scribe's name, Ka-Irw-Khufu (Kah er Küfü).

This story gives students some historical perspective on the development of calculation and number ideas in early cultures. Students will realize that the number system they are familiar with developed over many years. Too often, students think of mathematics as a body of stagnant knowledge that has been in existence since the beginning of time. Instead, it is a continually evolving science with many ways to approach computation and solve problems.
The Egyptian system is an example of this. Until recent times (the 19th century) very little was known about the early Egyptian and Sumerian cultures because we could not translate what they had written. As historians of Egyptian mathematics and anthropologists have found methods to translate the Egyptian writing, they have come to understand that these early people knew a great deal of mathematics. Many of these ideas were later credited to other cultures and mathematicians because the Egyptian ideas had been lost when people could no longer read the Egyptian writing called hieroglyphics.
The story sends Phil, Howard, and Professor Peabody back into the time of the fourth dynasty around 2550 BCE.

The Phil and Howard's Excellent Egyptian Adventure story is introduced here to give all students an introduction to the use of a different multiplication strategy that comes from another time and culture. Students who are confident with the methods on the strategies menus can be challenged to use the story as the context for learning a new method using Questions 28–30.
Discuss the story using the following prompts:
Page 509
- Solve 21 × 14 using any method you choose. (294; Methods will vary.)
Page 512
A statue of the scribe Ka-Irw-Khufu was excavated from the area of the great pyramid at Giza and is now owned by the Cairo Museum. Scribes were men who created many of the papyrus scrolls that include examples of the way Egyptians used their number system to solve problems. There is evidence that these scribes held highly honored positions in the government and may have been sons of the royal family. The statue of Ka-Irw-Khufu dates from the fourth dynasty (2544 BCE) during the period when the great pyramids were being built.
Page 515
It is hard to remember in our paper-strewn world that people long ago developed their systems of computation without this bountiful supply of writing materials. The papyrus Ka writes on was made by collecting the papu reeds from along the banks of the Nile river, slicing them into long thin strips, and laying them side by side. Then a second layer of strips was laid crosswise on top and the whole piece was soaked in water, pressed, and sun-dried. After the papyrus dried, it was prepared for writing by carefully smoothing it with a hard, round object. These sheets were far too valuable to be used as scratch paper. When they were ready, the scribes crushed the end of a smaller reed to make a brush that was dipped in ink to paint a more cursive form of these symbols onto the paper.
Page 517
You may wish to have students try writing and reading some numbers written in hieroglyphics before you continue the story. Use the Egyptian Numbers and Symbols Master to discuss how Egyptian numbers are formed. Make a few numbers using the Egyptian symbols and have students tell you what number is represented. Then ask students to make the Egyptian symbols for various numbers.
- When Phil writes 3527 with Egyptian symbols, he organizes them from left to right in groups. Is this necessary? Why or why not? (No, it's not necessary because each multiple of ten is represented with a different symbol. Order doesn't matter.)
Ask a student to use Egyptian symbols to write 3527 in an order that is different from that of Phil's, emphasizing that the order of the symbols does not matter.
- Which is easier to read—[student name]'s notation or Phil's? Why? (Opinions will vary, although it is probably easier for us to read the symbols when they are organized Phil's way because we read the larger numbers first, from left to right.)
Explain that Egyptian symbols, like Hebrew symbols, are written from right to left.
- How is the Egyptian system and our number system similar? Different? (Both systems are based on tens. Our system has different symbols for 1, 2, 3, 4, 5, 6, 7, 8, and 9, but the Egyptian system uses tally marks for these numbers. The Egyptian system uses unique symbols to show tens, hundreds, and thousands, but we use the same symbols. Our system relies on the position of the digit to determine its value, but the Egyptian system does not have to.)
Note that Professor Peabody changes the original problem into a problem that will make more sense to someone in Ka's time.
Page 518
This page presents the first explanation of the process of duplation that Egyptians used to multiply large numbers.
See Content Note.
- Has Ka calculated correctly? (Yes)
- Has he used the correct symbols for 21? 42? 84? 168? (Yes)
- Write the Egyptian hieroglyphic for 294 using the smallest number of symbols possible. (The notation written by Ka is correct.)
- Use Ka's method to find 12 × 21.
Duplation. In the story's problem, 14 × 21, students may wonder why Ka doubles 21 and not 14. Either factor could be doubled to find the product 294; however, doubling the larger number, 21, results in fewer steps.
For example, 7 × 21 could be solved by either doubling 21 or by doubling 7.
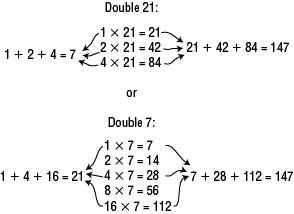
First, make a table of the doubles of 21. Then, since 8 + 4 = 12, add the products of 8 × 21 and 4 × 21 to find the product of 12 × 21. See Content Note.
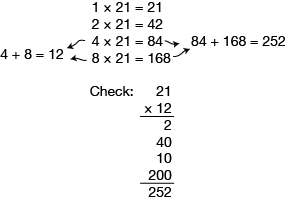
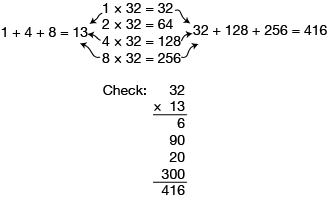
Show students other examples of the duplation method. Try 7 × 32. Make a table of the doubles of 32. Since 1 + 2 + 4 = 7, add the products of 1 × 32, 2 × 32, and 4 × 32 to find the product of 7 × 32.
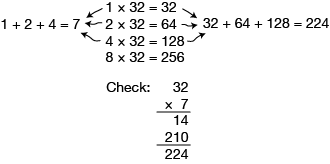
Challenge students to find 13 × 32:
Page 519
- What is the double of 84? (168)
- How does Ka record this? (He gathers the 16 ten symbols together and replaces them with 1 one hundred symbol and 6 ten symbols.)
- How is this like our regrouping? (It is the same. When we get 10 ones, we can regroup and make 1 ten. When we get 10 tens, we can regroup and make 1 one hundred.)
- Why does the idea of writing nothing confuse Ka? (When Ka has nothing, he doesn't have to write anything.)
- Why do we need to have a way to write nothing? (In our number system, we use the same symbols for ones, tens, and hundreds; the place is important. If there is no value for one of the places in the middle of the number, we need a way to show that the position is empty. This is the difference between a number system where position is used to identify the numbers and one in which position is not used to identify value.)

Zero. As with the Romans, Egyptians had no symbol for zero. They changed symbols to signify value. In the Hindu-Arabic system, when we write 430, we know the 3 is three tens since it occupies the second position from the right. The zero shows us that there are no ones.