Estimate First. Write the following problem on the board and ask students to estimate the answer.
57 × 8
Ask students to share their strategies and estimates. Display the two most common strategies for this problem.
- Round 57 to 60 and multiply: 60 × 8 = 480
- Round 8 to 10 and multiply: 57 × 10 = 570
Tell students not to find the exact answer yet. Probe their number sense.
- Do you think 480 is higher or lower than the exact answer? Why? (Higher, because we rounded 57 up to 60.)
- Do you think 570 is higher or lower than the exact answer? Why? (Higher, because we rounded 8 up to 10.)
- Which do you think is the closer estimate? Why? (480 has to be closer. If both estimates are high, then 570 is even higher than 480.)
- Which is easier for you to multiply in your head? Why?
Revisit Three Multiplication Methods. Now tell students to find the exact answer using the all-partials method. Remind students that they studied the all-partials method in Unit 7. Ask a volunteer to come to the board and solve the problem using this method. Figure 1 shows two possible solution paths. Ask the student to explain each step of the solution. Have the class ask the volunteer to clarify any steps.
If needed, supplement student questions with questions similar to the following:
- What did you do first?
- Where did you get the partial product 56? (I multiplied 8 times 7.)
- How do you know it is 56 and not 560? (Possible response: Because the 8 and 7 are in the ones place, not the tens. It is just 8 × 7 = 56.)
- How did you get the partial product 400? How do you know it is not 40? (Possible response: 8 × 50 = 400; The 5 is in the tens place, so you have to multiply 8 × 5 tens. 8 × 5 tens is 40 tens or 400.)
- What was the last step you did to get your final answer? (Possible response: I added 400 and 56 to get 456.)
- Which of our estimates was closest? (60 × 8 = 480)
- Work with a partner. Find a way to use mental math or a few quick notes to find an exact answer to check the problem. (Possible response: Multiply 8 × 60 to get 480 and then subtract 3 × 8, or 24. 480 - 24 = 456.)
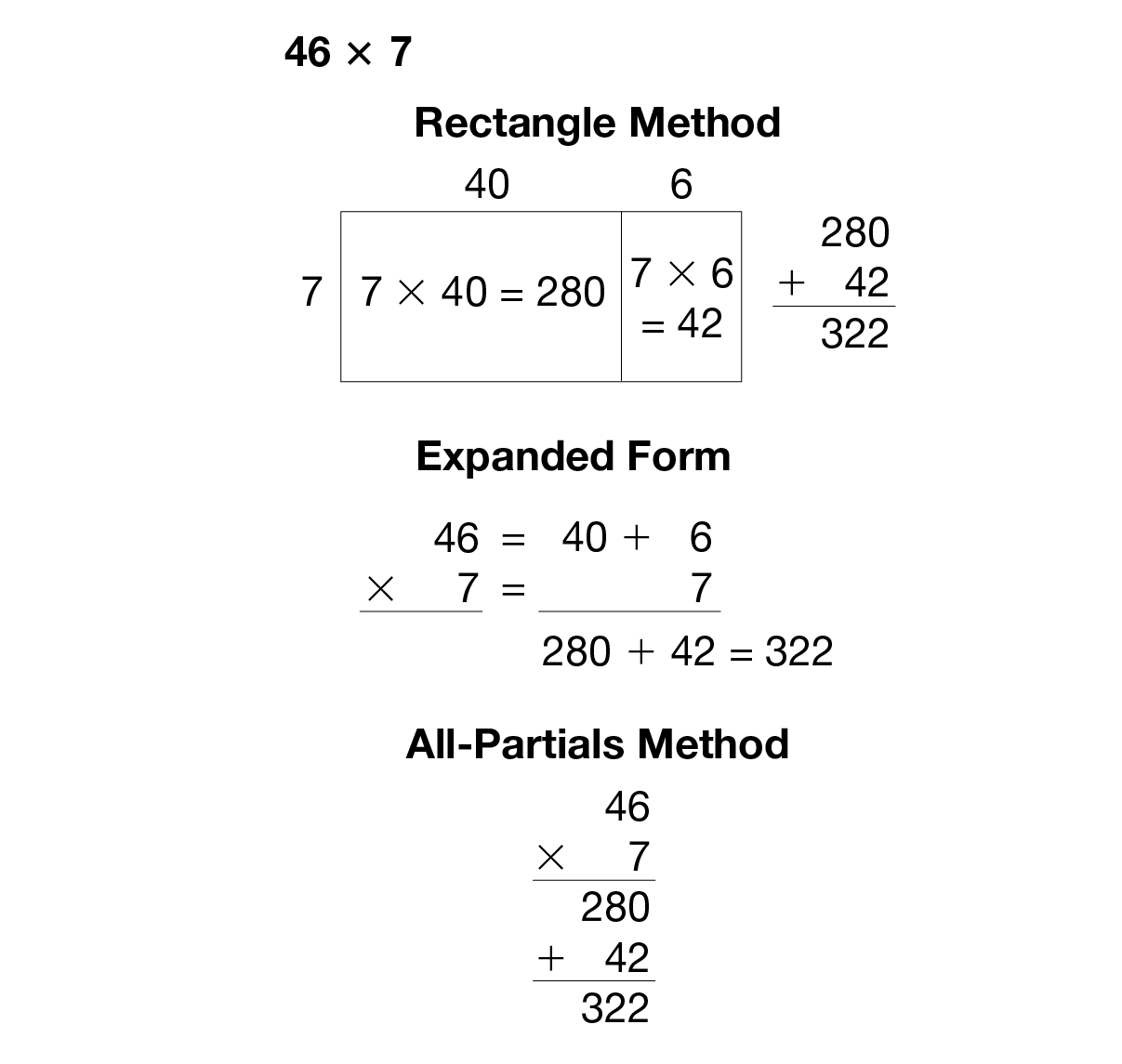
- Solve 46 × 7 three ways using the rectangle model, the expanded-form method, and the all-partials method.
They should share their answers and partial products within their group. Have student volunteers demonstrate each method for the class. See Figure 2.
- What is the same about the three methods? (Possible responses: They all break the two-digit number into tens and ones. They all have the same partial products. They all add the partial products. They all reach the same answer.)
- What is different? (The all-partials method does not write out the partition of a number into tens and ones—both other methods do; the rectangle model uses a diagram but the other two do not.)