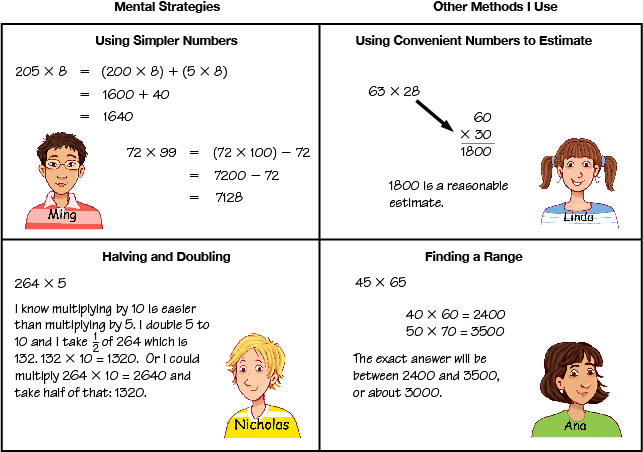
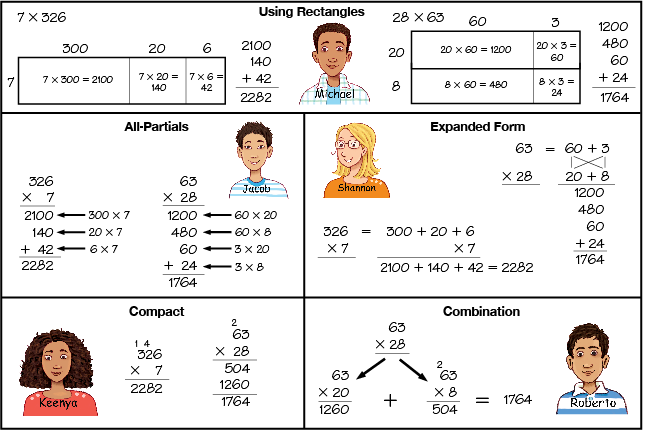
Use Mental Math and Estimation. Ask students to get out the My Multiplication Menus they created in Lesson 2. Refer them to the Multidigit Multiplication Strategies Menus in the Reference section of their Student Guides. See Figures 1 and 2.
Display the Multidigit Multiplication Strategies Menu: Mental Math and Estimation Master and use the prompts below to compare the student-created menus to it.
- Look at the menu you made and the menu in the Reference section of your Student Guide. Which strategies on your menu are also on the menu in your book?
- Work with a partner. Use Linda's strategy on the menu in the book to estimate the product of 98 × 54. (Possible estimate: 100 × 54 = 5400.)
- Decide if the exact answer will be larger or smaller than your estimate. How do you know? (Smaller, because I rounded 98 up to 100.)
- Use Ming's strategy to find an exact answer for 98 × 54 using mental math or a few quick notes. (100 × 54 = 5400; 5400 - 108 = 5292)
- Choose a strategy from one of the menus to solve 12 × 21 using mental math or a few quick notes. (Possible response: 12 × 20 = 240; 240 + 12 = 252)
Use Paper-and-Pencil Methods.
Display the Multidigit Multiplication Strategies Menu: Paper-and-Pencil Methods and use the prompts below to compare the student-created menus to the menu in the Reference section of their Student Guides.
- Look at the menu you made and the menu in your Student Guide. Which paper-and-pencil strategies on your menu are also on this menu?
- Which method have we not talked about in class for two-digit by two-digit numbers? (compact method)
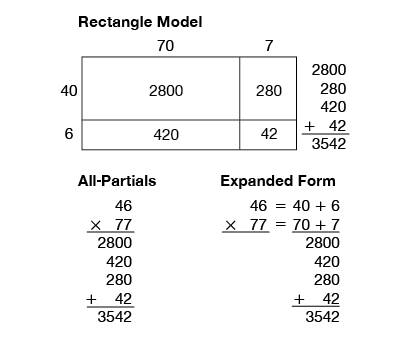
- Solve 46 × 77 using one of the three paper-and-pencil methods: using rectangles, all-partials, and expanded form. (46 × 77 = 3542. See Figure 3.)
Be sure that all the methods are represented. Choose a student
for each method and ask them to write their solutions on the
board.
- Are the answers reasonable? How do you know? (Possible response: I estimated by rounding both answers down and both answers up. 40 × 70 = 2800 and 50 × 80 = 4000. 3542 is in between, so it is reasonable.)
- How are the methods alike? (They all give the same answer. They all have the same partial products.)
- How are they different? (Possible responses: You don't have to write as much for the all-partials method or draw rectangles.)
- Which ones can help you keep track of the partial products, so you know when you have found them all? (using rectangles and expanded form)

Use Self-Check: Questions 1–2 in the Multiplying by Multiples of Ten section in the Student Guide and Self-Check: Questions 1, 5, and 13 in the Moving Ahead with Multiplication pages in the Student Activity Book to assess students' abilities to demonstrate understanding of the place value concepts and mathematical properties involved in 2-digit by 2-digit multiplication [E1], showing connection between models and strategies [E2], estimating products [E3], and multiplying multidigit numbers using mental math strategies and paper-and-pencil methods [E4].