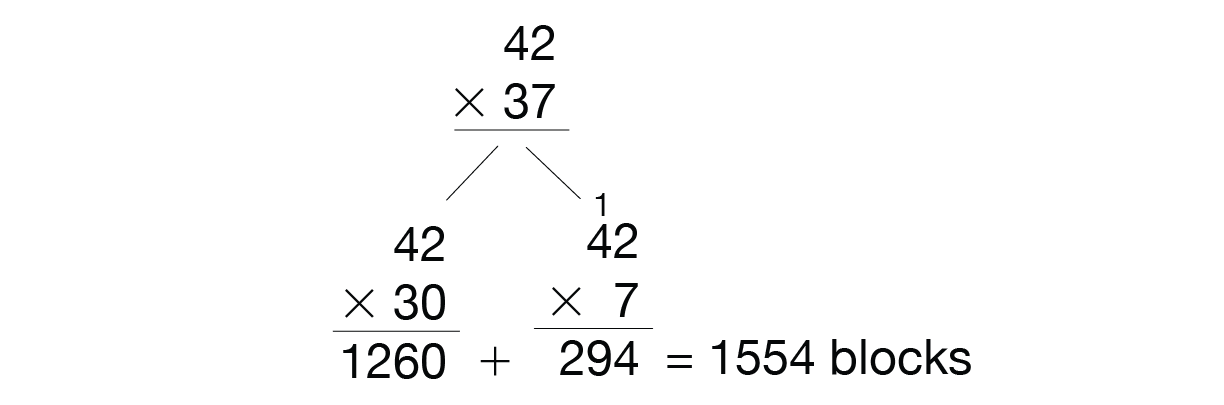Review the Paper-and-Pencil Method of Multiplication. Discuss with the whole class the vignette at the beginning of the Compact Multiplication Revisited pages in the Student Guide. Begin by asking students about estimation strategies. Question 1 asks students to analyze a fairly typical estimate for 7 × 96 blocks (7 × 100 = 700).
The next part of the vignette discusses different methods for solving the problem.
- What multiplication problem are the students trying to solve? (96 × 7)
- What are the partial products in Jackie's method? (7 × 6 = 42; 7 × 90 = 630)
- In Jerome's method? (7 × 6 = 42; 7 × 90 = 630)
The beginning of this lesson reviews compact multiplication of 2-digit numbers by 1-digit numbers, first studied in Unit 7. Allocate time for this discussion as needed by your students. If your students are comfortable with the compact method for these problems, briefly review and move on.
Ask students to work in pairs to read the explanation of Maya's compact method that follows Question 2 and discuss Questions 3 and 4.
As students explain the differences and similarities between the three paper-and-pencil methods, ask them to think about the benefits and drawbacks of each.
- Which method do you prefer to use? Why?
- Which method was easier for you to learn?
- Which makes more sense to you? Why?
- Which method helps you multiply more accurately? (Students may say that writing out the partial products keeps them from making mistakes.)
- Which method helps you estimate quickly?
- Which method helps you multiply more quickly? (Students may say that the compact method is the fastest.)
Ask students to discuss Question 5 in pairs. As they discuss the answers, talk with individual students to check for understanding of the steps in the compact method. Spend as much time on this question as necessary to ensure that students understand the steps of this method, particularly those steps that are not written down.

As student pairs discuss the answers for Check-In: Question 5, look for language that demonstrates understanding of the place value concepts involved in multiplication (E1). Use discussion prompts similar to the following to probe students' thinking:
- For Question 5A, where did John get the little 3 he wrote above the problem? (He multiplied 6 × 6 and got 36. It's the 3 tens in 36.)
- What does the 3 in 36 stand for? Does it stand for just 3 blocks? (It stands for 3 tens or 30 blocks.)
- Why did John write it above the 7? (He put it in the tens place. The 7 in 76 is in the tens place.)
- Question 5B asks how John got the 5 in the tens place in the answer. What was he thinking? (He thought 6 times 70 is 420 and add in the 3 tens or 30 from the first step. 420 + 30 = 450. Now there are 5 tens.)
- Question 5C asks about the hundreds place in the answer. What does the 4 in the hundreds place stand for? (400)
- How did John get the 4 in the hundreds place? (It comes from the 450 he got when he multiplied 6 times 70 and added in the 3 tens.)
The Workshop in Lesson 3 provides students targeted practice using conceptual models to represent multidigit multiplication.
Question 6 provides more practice multiplying by single-digit numbers before students begin using the compact method to multiply by two-digit numbers. Remind students to consistently use mental math and estimation strategies to check the reasonableness of their answers. Question 7 reinforces this habit.
Explore the Combination Method. Use Questions 8–9 as an introduction to the compact method for multiplying multidigit numbers. These questions discuss what is called a “combination” method. The problem (42 × 37) is broken into two simpler problems by partitioning one number into tens and ones: 42 × 7 and 42 × 30. See Figure 1.
Here, one problem is solved using the compact method (42 × 7); the other can be solved using a strategy involving multiples of ten. The two products are then added together to get the answer.
The “combination” method is included here because it leads directly into a discussion of the compact method. The twopartial products are the same as when solving the problem using the compact method. Do not spend too much time on this method. It is not intended to be adopted as yet another paper-and-pencil method with which all students are expected to be proficient. If some students pick it up and continue to use it, that is good, but not necessary.
- Where have we seen numbers broken into tens and ones before multiplying? (Using the expanded-form method.)
- Why are the two new problems easier to solve than the first one? (It is easier to solve a problem in which one number has just one digit. When one of the numbers has a zero, like 30 in this problem, it is just like multiplying by one digit, except that when you are done you multiply the answer by 10, adding a zero to the end of the answer.)
- How is this method different from the expanded-form method? (Only one of the numbers to be multiplied is partitioned into tens and ones; in the expanded form, both are partitioned into tens and ones.)
- What are the partial products in this problem? (1260 and 294)
- How did we get each of the partial products? (30 × 42 = 1260 and 7 × 42 = 294)
Have the students solve the problems in Question 9 in small groups and ask different groups to demonstrate the solutions for the class.
Introduce the Compact Method with Two-Digit Numbers. After students have estimated the product of 24 × 12 in Question 10, have them read through the discussion of Nicholas's compact method for solving 24 × 12. In this first problem, there are no carries.
Questions 11–12 lead students to observe that the product of each smaller problem in the “combination” method corresponds to the partial products in the compact method. In essence, the two methods are the same. Both methods partition one of the numbers into tens and ones before multiplying. In the compact method, the partition is not written down as separate problems, but is made mentally.
Have students solve the problem 74 × 23 in Question 13 using the all-partials method. Then read through the explanation of Nicholas's compact method solving the same problem. In this problem, there are two carries. You may want to go through all the steps listed in the Student Guide with a few other problems that involve carries before moving on.
Questions 14–18 provide more practice with the compact method. Students can work in groups to compare answers. Students solve Check-In: Questions 19–20 independently.
Use Check-In: Questions 19–20 to assess students' progress estimating products [E3] and using paper-and-pencil methods to multiply [E4, E5].
Targeted practice for Expectations 3 and 4 is in Lesson 3.