Conceptual Understanding Necessary for Multiplication

Students were first introduced to the rectangle model for multiplication in Unit 3 when they explored rectangular arrays. Arrays helped them understand multiplication as finding the number of objects in a collection of equal-size groups. An array is a collection of objects arranged in equal rows. Students have used arrays since second grade to represent multiplication. They are useful in showing how to break apart a multiplication problem to make it easier to solve. This strategy is reviewed in the Daily Practice and Problems (DPP) for this unit to represent math facts strategies. See Figure 1 and DPP item B.

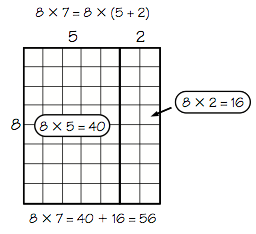
By learning this strategy and using this representation, students become acquainted with the distributive property. Understanding this property provides one of the keys to early algebraic thinking. The distributive property of multiplication over addition states:

Figure 1 provides a picture of the distributive property when 8 × 7 is rewritten as 8 × (5 + 2):

The distributive property is the basis of procedures for multiplying larger numbers. The product of 6 × 23 can be written 6 × (20 + 3) = (6 × 20) + (6 × 3) = 120 + 18 = 138. This is represented using rectangles as shown in Figure 2.

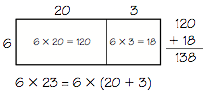
Students do not need to be able to recite or name the distributive property to use the concepts effectively when they multiply. However, it is important for them to be able to use the property to flexibly decompose products in this way.

Rectangle Model for Multiplication

In previous units, students learned to use the rectangle model to represent and solve multiplication problems consisting of two- and three-digit numbers multiplied by a single-digit number. In this unit, students expand the array and rectangle models to model multiplication of two-digit by two-digit numbers. See Figure 3.

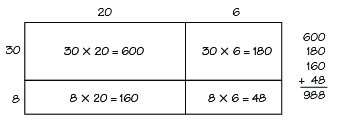
The partial products that students compute and display in the rectangle model provide them with a visual picture of the place value concepts (26 = 20 + 6; 38 = 30 + 8) and of the partial products involved when using paper-and-pencil methods.

Paper-and-Pencil Methods

In Unit 7, students solved multiplication problems using paper-and-pencil methods: expanded form, all-partials, and compact. They solved problems in which one of the numbers was a one-digit number and the other was a two-, three-, or four-digit number, such as 79 × 6 and 2116 × 7.

In this unit, students extend these paper-and-pencil methods to solve problems in which both factors are two-digit numbers, such as 47 × 36. Students often demonstrate varied levels of proficiency with these methods as they learn how to use them. When following rote computational procedures, it is typical to forget the underlying concepts and simply perform the algorithm. Performing procedures without understanding results in error-prone algorithms and poor retention. Children, therefore, need to understand the underlying ideas behind the algorithms so that their knowledge about multiplication can be expanded (National Research Council, 2001).

A focus in this unit is to ensure that students have a conceptual foundation for the procedures they use to multiply multidigit numbers. To this end, students develop a menu of strategies. They explore mental math strategies and visual models for multiplication, they work with paper-and-pencil strategies to improve efficiency, and they describe connections between these methods. They are asked frequently to compare the steps of one method to another and to describe the meaning of the steps they are performing. For example, students who understand the all-partials method should be able to correlate it with a rectangle model to show where each of the partial products comes from as shown in Figure 4.

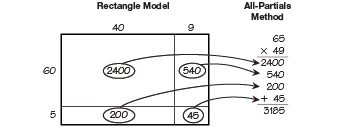
Developing varied strategies allows students to extend the place value concepts and number properties involved in multiplication to larger numbers. As students multiply using the expanded form, for instance, place value is highlighted as central to the process of multiplication. Students understand that procedures for multiplying 38 × 24 do not involve multiplying a “3 by a 2,” but rather 3 tens by 2 tens, or 30 by 20. Similarly, the expanded form emphasizes the role of the distributive property in multiplication, e.g., each partition of 38 (30 and 8) is multiplied by each partition of 24 (20 and 4). See Figure 5.

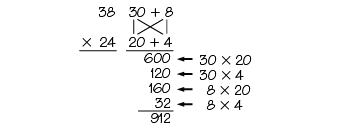
Experiences with multiple methods and representations allow students to develop a deeper understanding of the multiplicative process. This deeper understanding ensures that they maintain their ability to recognize and correct errors as they develop fluency with the algorithms and implement mental math shortcuts. See also Figures 1 and 6 in the Unit 7 Mathematics in this Unit section and the related text for a discussion of the interconnectedness of the methods.

Estimation Strategies

As in the earlier units on multiplication, estimation skills are developed and practiced in tandem with computational skills. The ability to estimate sums, differences, and products supports efficient and accurate computation and vice versa. Remind students of the situations in which estimation can and should be used to solve problems. These include:

Written work from field test classrooms reveals some students' misconceptions about estimation. For example, students wrote answers similar to those shown in Figure 6 when asked to estimate a problem such as 27 × 12.

Student A does not understand the purpose of the estimation—to mentally find a product quickly that will be close to the exact answer. This student is following a misunderstood procedure of changing each number in the problem and then multiplying. He or she does not know to choose convenient numbers that will be easy to multiply mentally.

Student B chooses convenient numbers but is not able to multiply them mentally or relies on the compact method when it is not appropriate.

Some students find estimates but do not use them to check for reasonableness. In their written work, they show estimates that are not close to their exact answers, but they do not make an effort to correct their work. These students demonstrate an overreliance on procedures they do not understand. For students to use estimation efficiently, they must be confident with a range of flexible methods and understand when it makes sense to apply them. Students' abilities to apply flexible methods are often impeded by having them learn procedures like the compact method before they have opportunities to learn more conceptual and transparent methods. Overemphasis on the compact method can decrease students' understanding of the conceptual basis of multiplication and consequently reduce their abilities to estimate and use mental math.

Ultimately, students should be able to choose appropriately from mental math, paper-and-pencil methods, and estimation to solve problems. Lesson 5 offers opportunities for students to make these choices based on the context of the problem. When solving a problem that requires a paper-and-pencil computation or the use of a calculator, the goal is that students formulate a mental estimate to check the reasonableness of the answer.

Balancing Learning and Practice

Children should be able to understand the procedures they are performing, to make good estimates, and to know when to turn to a calculator for an exact answer (NCTM, 2000; National Research Council, 2001).

It is important for students to improve accuracy and efficiency with multidigit multiplication. According to the National Research Council, “Practice is important in the development of mathematical proficiency. When students have multiple opportunities to use the computational procedures, reasoning processes, and problem solving strategies they are learning, the methods they are using become smoother, more reliable, and better understood. Practice alone does not suffice: it needs to be built on understanding and accompanied by feedback. In fact, premature practice has been shown to be harmful (National Research Council, 2001, p. 422).

Based on the recommendations cited above and other research, Workshop Lessons were developed to provide practice based on students' current skills and concepts according to their progress on the unit's Benchmark Expectations. This avoids “premature practice” by assuring that practice is targeted to students' needs at the time. The Expectations offer a framework for providing useful feedback to students in conjunction with the practice.

In this unit, students practice multiplication in the DPPs, in the Lesson 3 Workshop, and throughout the unit to build computational skills. Students should do these problems thoughtfully, using multiple methods, rather than rush through a page of calculations without checking for errors or considering the reasonableness of their answers. If students practice incorrect procedures, it is more difficult for them to learn correct ones (National Research Council, 2001). Students also develop fluency with algorithms at different rates. Lack of fluency should not be a deterrent to moving on to different topics.