Choosing Strategies to Multiply

Est. Class Sessions: 2

Developing the Lesson

Part 3: Choosing Strategies to Solve Problems

Planning Your Strategies. With the class, read the instructions for solving the problems in the Victory Videos section in the Student Guide. Point out to students that deciding which method to use will be an important part of this activity.

Look over Questions 1–7 with the class. Ask students to use the Planning Your Strategies page in the Student Activity Book to keep track of the strategies they choose for each problem.

Begin a class discussion about choosing strategies by asking:

For which of the problems in Questions 1–7 would you use an estimation strategy? (Question 3 and Question 5)
Why is estimation a good strategy for these problems? (Students may respond that we need only to find a quick answer in our heads, or that it is impossible to find an exact answer because the numbers that are given in the problem are not exact.)
Which type of estimation strategy would you use for Question 3? (Answers may vary. Using convenient numbers would allow a mental calculation of one half of 6 × 10 × 100, or about 3000.)
Which type of estimation strategy would you use for Question 5? (Finding a range makes the most sense since the number of employees at each store is given as a range of numbers.)

Have students write these strategies in the boxes for Question 3 and Question 5 on the Planning Your Strategies page.

Then ask:

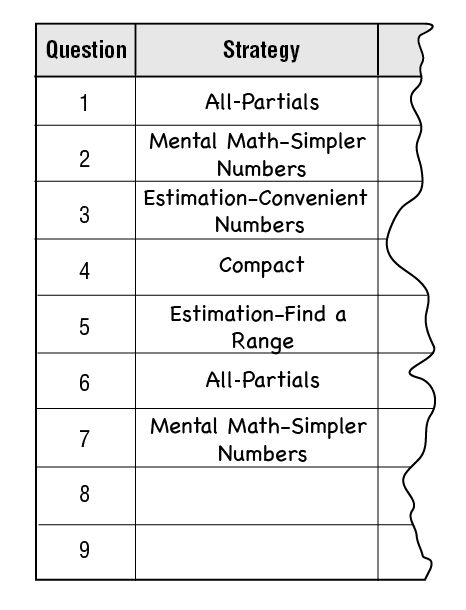
For which of the problems in Questions 1–7 would you use a mental math strategy? (Answers may vary. Any of the problems might be solved using mental math, though Questions 2 and 7 lend themselves to solving by using simpler numbers.)
Why is mental math a good strategy for these problems? (Students may respond that some of the numbers in these problems are close to convenient numbers.)

Have students write their strategies in the boxes for any questions they decide to do with mental math. Continue this discussion until students have strategies written for each of Questions 1–7 on the Planning Your Strategies page. At this point, students' tables may look like the one in the example in Figure 1.

Some students may key in words such as “about,” “around,” or “between” to help them decide when to estimate. Using key words can be a helpful signal, but encourage students to understand the whole problem before deciding whether or not to estimate. Searching for key words does not necessarily help students comprehend the meaning of the problem, and at times it can lead students astray. For example, students may want to estimate when asked to find the distance around a square with a side length of 25 meters because they see the word “around,” even though the meaning of the problem does not suggest estimation.

Solve Using Appropriate Strategies. Once students have selected strategies for the first seven problems, they solve those problems using the strategies they chose.

Before students continue to solve the problems in Questions 8–27 (in the Visiting Ancient Egypt, Counting Chairs, and Ordering School Supplies sections), have them work with partners to decide on strategies for each of those questions. Remind students of the following:

Use each of the nine strategies at least two times.
Keep track of how many times each strategy is selected from the Strategy List with tally marks.
Start by finding the problems that can be solved by estimation.
Next, find problems that can be solved using mental math strategies.
Finally, select problems to solve using paper-and-pencil methods.
Use estimation to check for reasonableness of answers for problems solved using mental math and paper-and-pencil strategies.

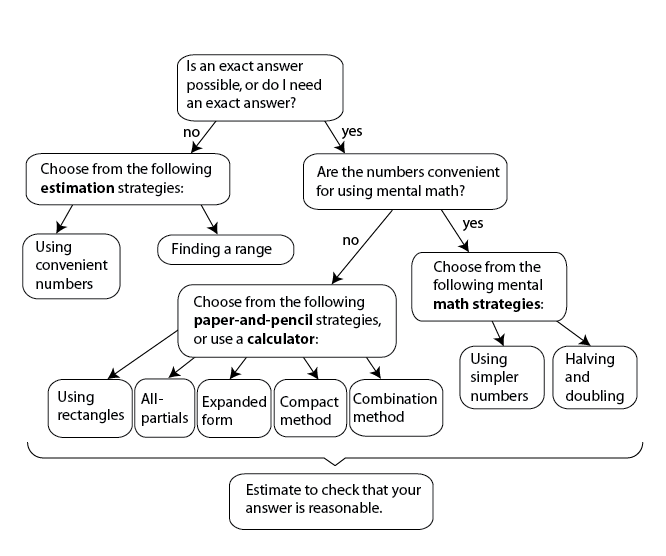
Figure 2 shows a process for choosing strategies. Use this chart as a guide for asking students key questions as they choose strategies for solving problems. Since the chart is visually complex, you may prefer to use it only as a teaching guide rather than giving it directly to students.

Students should select estimation strategies for Questions 3, 5, 10, 11, 21, 22, 26, and 27. These problems contain clues that finding an exact answer is either not necessary or not possible. See Content Note. All other problems can be solved by either paper-and-pencil strategies or mental math. Remind students to try to solve problems using mental math first. Students may show different comfort levels with mental math, but should be encouraged to practice mental strategies to increase their flexibility with computation.

A Note about Estimation. Estimating products involves multiplying with approximate numbers. How this is done depends on the problem being solved. In some problems, numbers may be given that are already an approximation of some quantity that is not known exactly. For example, in Question 10, the answer will be an estimate necessarily because it is clear that every camel is not able to drink exactly 30 gallons of water in exactly 15 minutes. However, the numbers given in the problem are relatively “friendly” and should not be rounded further before multiplying.

In other problems, students may first need to round exact numbers to friendly numbers so that a mental math strategy can be used to multiply. In Question 22, for example, it is possible to find the exact number of seats in the auditorium. However, an exact answer is not necessary in this problem, so numbers can be rounded first to make the multiplication simpler.

It is important that students understand estimation as a process of approximation rather than simply as “rounding before multiplying.” If quantities are already estimated as convenient numbers in a problem, further rounding may actually result in a less accurate estimate.

Once student pairs have chosen a strategy for each question, they use their chosen methods to complete the problems in Questions 8–27. Some flexibility is appropriate here. If students decide to try a different strategy than the one they originally chose, they should be encouraged to do so. For example, as students solve problems, they may notice something new that leads them to estimate or to use mental math. Remind students to check all answers for reasonableness by performing a quick estimation strategy.

Use Check-In: Questions 23–27 in the Student Guide to assess students' progress on the following:

Estimating products of multidigit numbers [E3].
Multiplying 2-digit by 2-digit numbers using mental math strategies and paper-and-pencil methods (e.g., expanded form, all-partials) [E4].
Multiplying 2-digit by 2-digit numbers using the compact method [E5].
Choosing appropriately from among estimation, mental math strategies, and paper-and-pencil methods to multiply multidigit numbers [E6].

Multiply Using a Doubling Table. After students have completed the questions using their chosen strategies from the menu, have them use the doubling table method to solve Questions 28–30. Any problems not finished by the end of the first class session can be completed for homework.