Identify Rules in Data Tables. Point out one milliliter on a graduated cylinder and 1000 ml on a liter bottle. Show students the function table you prepared before the lesson, and tell them that a container holds 5000 milliliters.
Use the function table to record student responses as you ask:
- Using what you learned in the previous lesson, how many liters does the 5000-milliliter container hold? (5 liters)
- How many liters does a 1000-milliliter container hold? (1 liter)
As the class completes the rest of the table, ask:
- What did you do to find the number of liters? (Answers will vary, but may include: I know that 1000 milliliters is equal to 1 liter so I used a pattern—if 1000 milliliters is 1 liter then 2000 milliliters will be 2 liters. Another possible response: I divide the number of milliliters by 1000 to find the number of liters.)
After the table is complete, tell students to:
- Write a rule to find the volume in liters when you know the volume in milliliters.
Record student responses for the class to see and compare. If students offer only one or two options, add a few more for them to consider. See Figure 3.
- With which rule do you agree? Why? (I agree with the rule that you divide the number of milliliters by 1000 to find the number of liters. I agree with this rule because the table shows this pattern.)
- With which do you not agree? Why? (I do not agree that the volume in liters equals the volume in milliliters minus 99 because 1000 milliliters minus 99 is 901 and 1000 milliliters is equal to 1 liter not 901 liters. I do not agree with the rule that the volume in liters equals volume of milliliters times 1000 because liters are much larger than milliliters and if you multiply 1000 milliliters by 1000 you will get 1,000,000 liters and that is way too big. I do not agree with the rule that the volume in milliliters equals the volume in liters plus 1000 because if you have 1 liter and add 1000 you will have 1001 milliliters and that is one milliliter too much.)
- Does the rule you agree with work for every input? (It should.)
As a class, come to consensus about which rule fits the data in the function table.
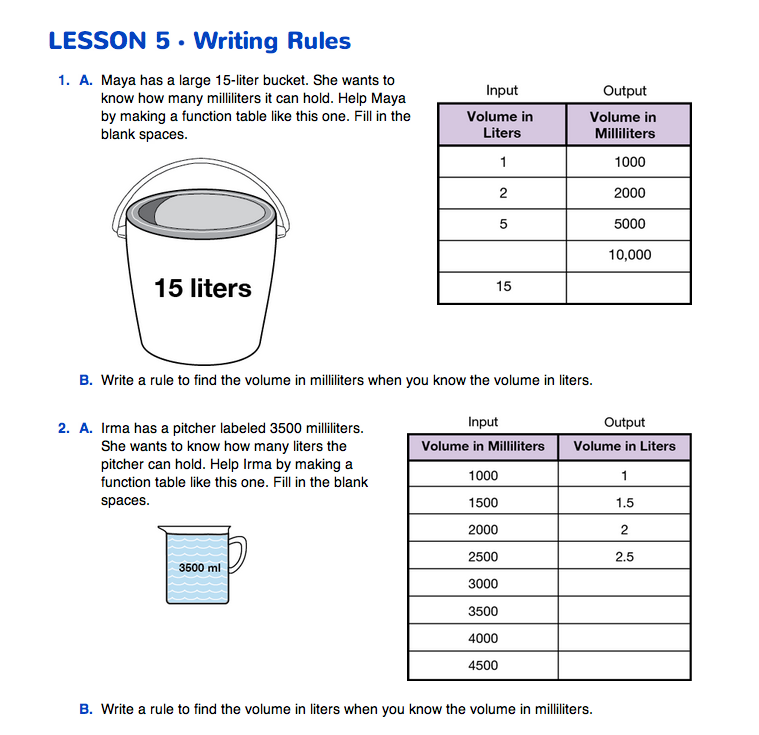
Write Rules. Introduce Maya's problem in Question 1 on the Writing Rules page in the Student Guide. Copy the table in Question 1 onto a display of the Function Table Master.
- How is Maya's situation different from the problem you just solved? (Maya is trying to find the number of milliliters in some number of liters, and in our problem we were trying to find the number of liters in some number of milliliters.)
Complete the table as a class and then ask students:
- Write a rule for finding the volume in milliliters when you know the volume in liters. (Possible response: Multiply the number of liters times 1000 to find the number of millileters.)
Again, record student responses for the class to see and compare. As a class, come to consensus about which rule fits the data in the function table.
- How can the rule for going from liters to milliliters help you write the rule for going from milliliters to liters? (Possible response: It is like a fact family. If the volume in milliliters equals the volume in liters times 1000, then the volume in liters equals the volume in milliliters divided by 1000.)

As students develop rules for function tables, encourage them to use words rather than letters as variables. When comparing different representations of the same variable (e.g., V for volume), letter variables can be confusing. So encourage students to write their rules in words.
Display the table in Question 2 on a Function Table Master. Introduce Irma's problem in Question 2. Ask students to complete the table together as a class and write a rule for Question 2B.
- If Irma's pitcher holds 3500 milliliters, how many liters does it hold? How do you know? (3.5 liters. Possible responses: I followed the pattern in the table. Or, I divided 3500 by 1000 and got 3.5.)
- Is this rule similar to any of the other rules we have written? (The rule is the same as that of the pattern we looked at in the beginning of the lesson.)
- Should it be the same? Why or why not? (Yes, it should be the same. To find the volume in liters when you know the volume in milliliters, you divide the volume in milliliters by 1000.)
Analyze Rules. Assign student pairs to solve and discuss Questions 3 and 4. For each function table in Questions 3 and 4, students are asked to test and choose appropriate rules offered by students in Mrs. Dewey's class. Then they use the rule to calculate a volume in a different unit of measure.
As students are working, review and discuss student responses using questions such as:
- Why does not that rule not work?
- What do the numbers mean in that rule?
- What do the letters in that rule mean?
- What would you tell Michael so he understands why his rule will not work for this pattern?
For Question 3, it will help students make sense of the rule if you use a 1-cup measuring cup and a quart container as references.
For Question 4, you may need to remind students of the correct order of operations. For Roberto's rule, they should first multiply 5 times the number of marbles and then add 25.