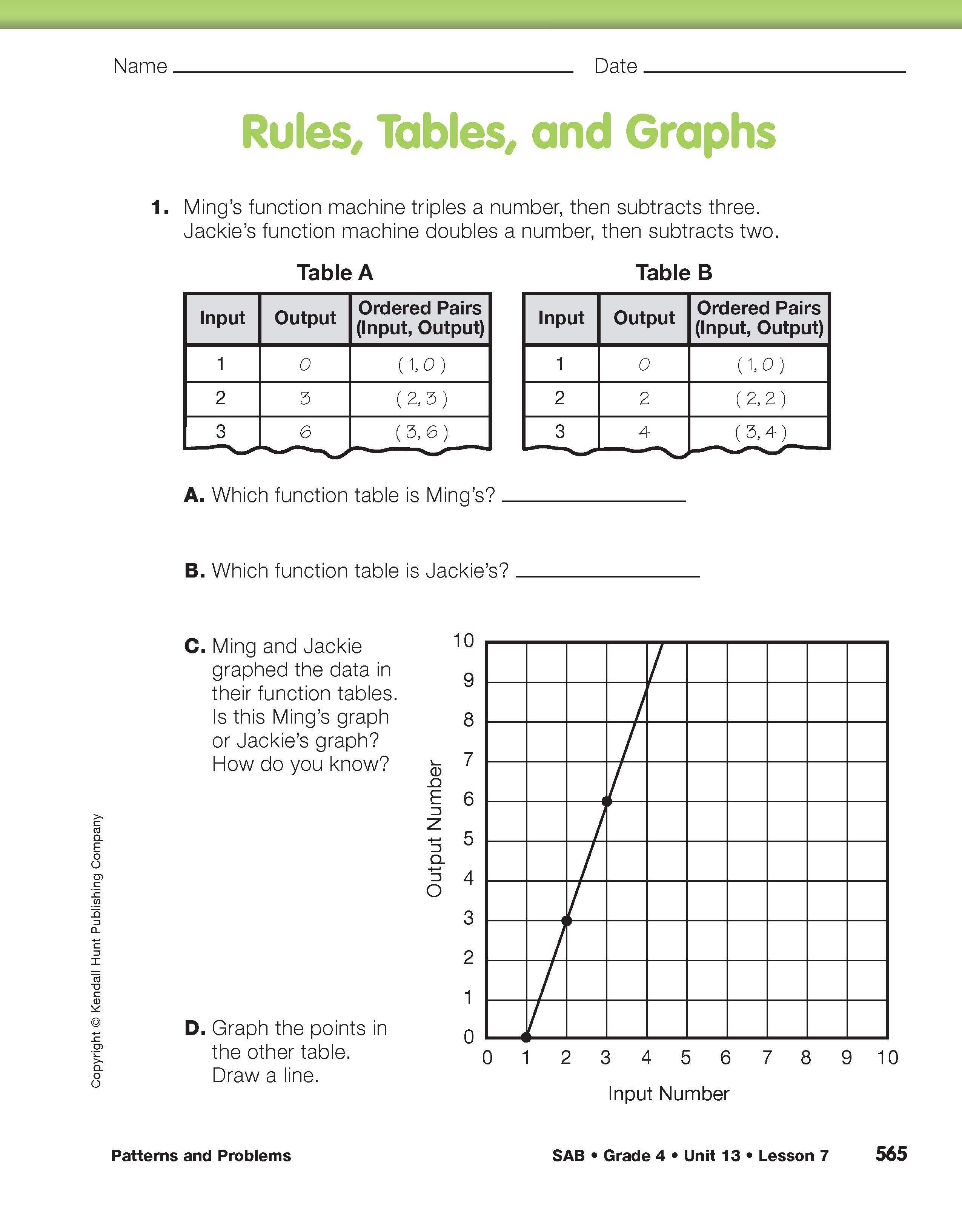
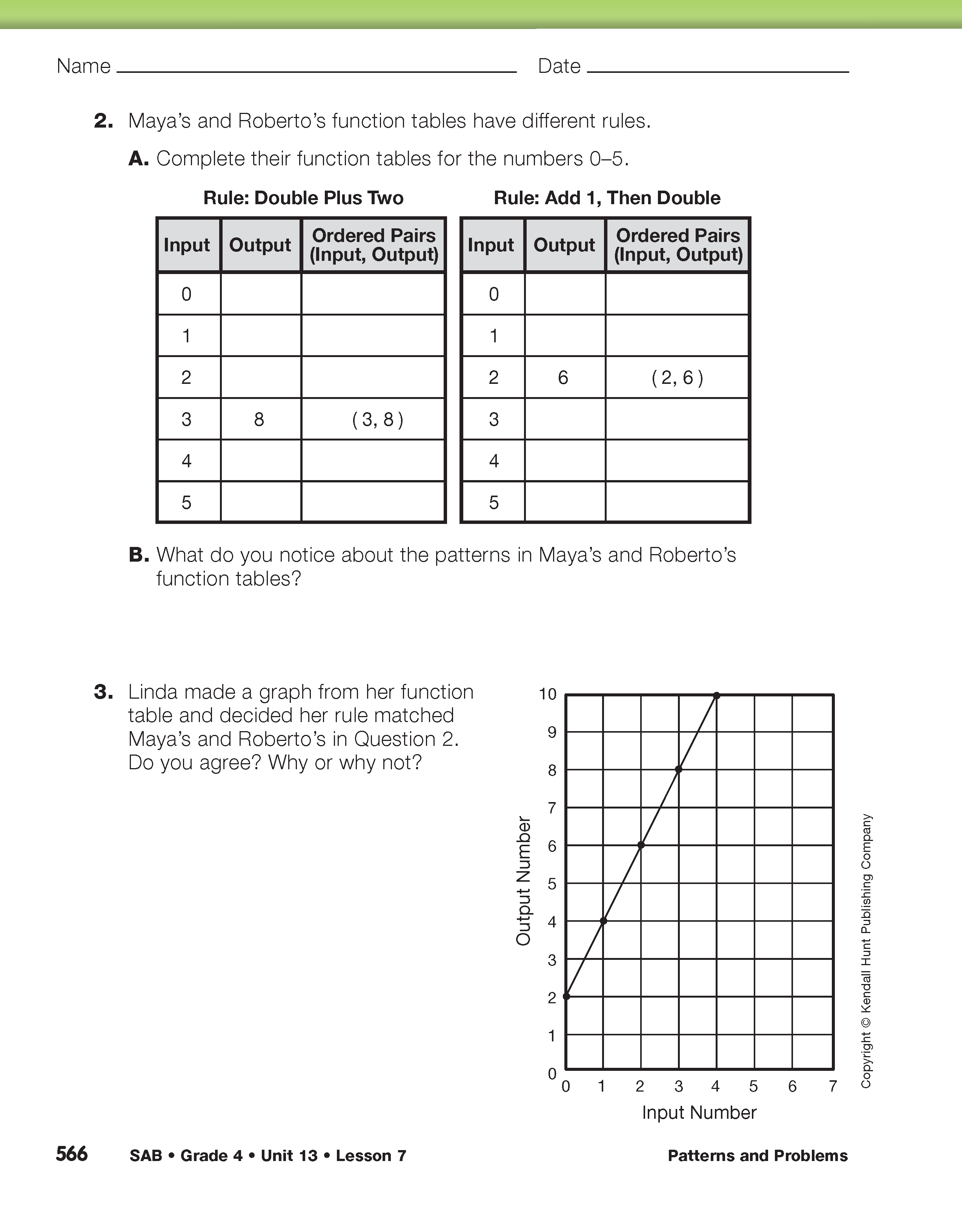
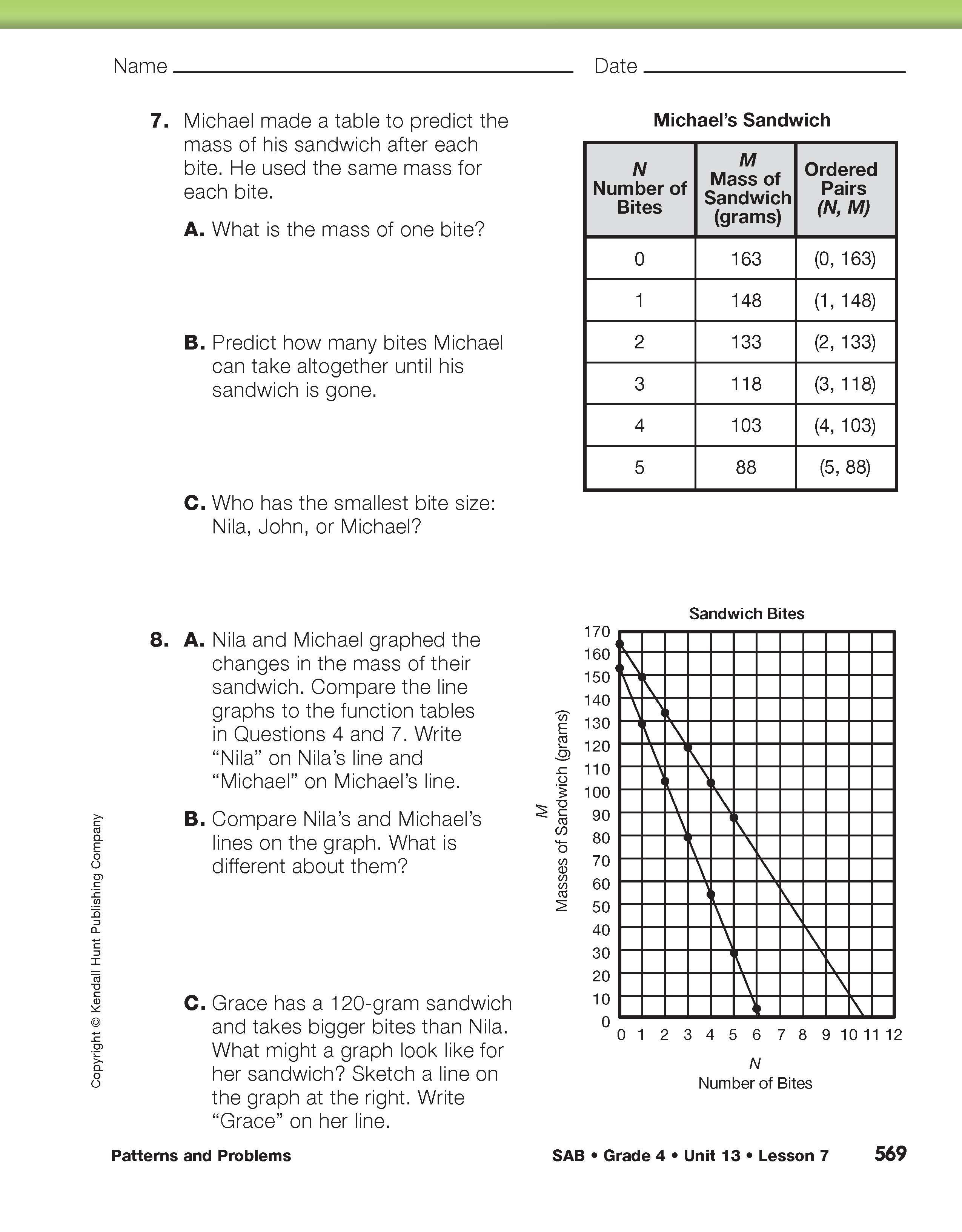
Identify and Compare Rules. Assign student pairs Questions 1–3 in the Student Guide. Remind students to use the order of operations.
After students have had a chance to identify the missing rules, compare Jacob's and Linda's tables and rules by asking:
- Did more than one of Jacob's rules work? (Yes, two of the rules worked, N + N + 5 and 5 + N × 2.)
- Why do both rules work? (Both say to do the same thing, just in different ways. Five is added to both and N + N is the same thing as N × 2.)
- Did more than one of Linda's rules work? (Yes, two of the rules worked, N + N + 10 and N × 2 + 10.)
- Why do both rules work? (Both say to do the same thing, just in different ways. Ten is added to both and N + N is the same thing as N × 2.)
- Looking at the two tables, how are they alike? (Possible responses: In both tables the output goes up by 2 for the next row or input.)
- Look at the rules. Why do both rules work? (When you multiply by 2, that's the same as doubling.)
- Looking at the two tables, how are they different? (Possible responses: For an input of zero, the output is different on each table. Or, each table starts differently.)
- Where does each one start? (Jacob's starts at 5 and Linda's starts at 10.)
- Look at Jacob's and Linda's rules. Where are these numbers in their rules? (Jacob adds 5 after he doubles and Linda adds 10.)
Compare Patterns in Graphs and Tables. Assign student pairs Question 1 on the Rules, Tables, and Graphs pages in the Student Activity Book.
After students have had a chance to figure out which rule belongs to each graph and which graph function belongs to the graph, ask:
- How do you know the line graph represents Ming's function machine? (Possible response: I matched up the data in the table with the data points on the table; or I noticed the “step” in the graph was 3 and Ming's table also has a “step” of three between points.)
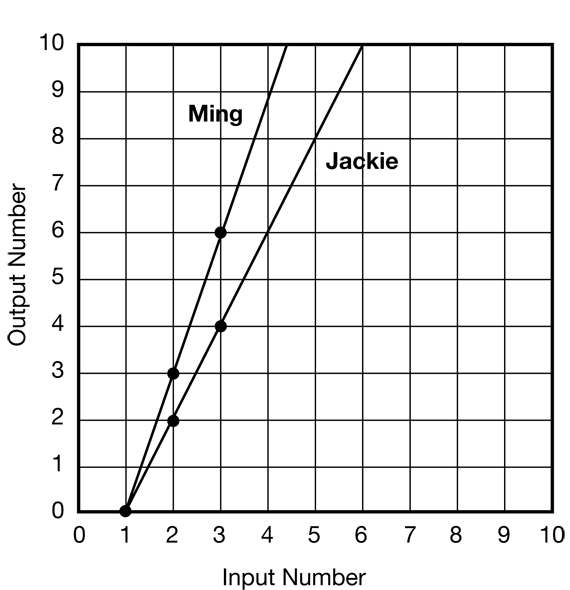
In Question 1D, students are asked to plot the points and draw a line graph to represent Jackie's function machine on the same graph. See Figure 1.
Referring to the line graphs, ask:
- How are they alike? (Both lines go through (1,0).)
- How are they different? (Possible responses: Ming's line is steeper than Jackie's, or they go up at different angles or slopes.)
Have students work with a partner to complete Questions 2–7 in the Student Activity Book.
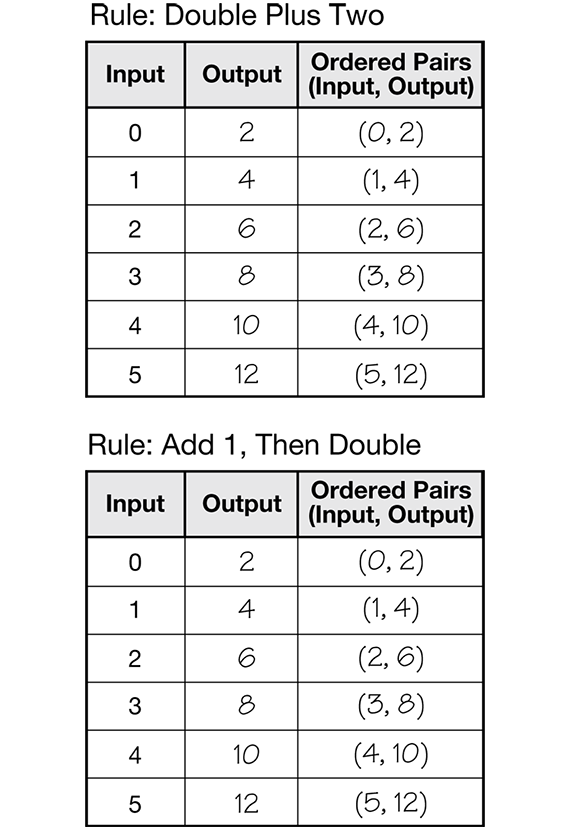
Discuss Patterns and Rules. After students have completed the questions, choose a couple of problems to discuss with the class. In particular, direct students' attention to Maya's and Roberto's function tables in Question 2. See Figure 2.
- Use a number sentence to write a rule for Maya's function table. (n × 2 + 2)
- Can you think of another number sentence for the function table? (n + n + 2 or 2n + 2)
- Use a number sentence to write a rule for Roberto's function table. (n + 1 × 2)
- What did you notice about the patterns in Maya's and Roberto's function tables? Explain. (The inputs and outputs are the same in each table. The lines on their graphs would be the same, too. Doubling the number and then adding 2 is the same as adding 1 to the number and then doubling.)
Direct students' attention to Question 5 and say:
- Use words to describe how you could find the mass of John's sandwich (M) if you knew the number of bites (N). (If I know each of John's bites is 30 grams, I can multiply the number of bites times 30. Then subtract that from 189 grams, the starting mass of the sandwich to find the new mass of the sandwich.)
- Use a number sentence to write this rule. (M = 189 − 30 × N)