Read The Crow and the Pitcher. Students begin the activity by reading the story of The Crow and the Pitcher section on the Measuring Volume pages in the Student Guide and discussing Questions 1–2. The crow can raise the level of the water in the pitcher because the rocks displace (or push away) the water. If the rocks have different volumes, they will displace different amounts of water.
Aesop's Fables, as compiled and illustrated by Jerry Pinkney, is a collection that includes The Crow and the Pitcher. The fable as it appears in the Student Guide is a retelling of the ancient story. There are many versions of this story with different morals. For example, some versions end with “Necessity is the mother of invention,” while others conclude with admonishments such as “Skill and patience will succeed where force fails.” Ask students to relate the story to problem solving: How did the crow solve the problem? How many strategies did he try? Did he give up easily?
There are many animated versions of The Crow and the Pitcher story available. Show students the animated version to better illustrate the action of displacement described in this story.
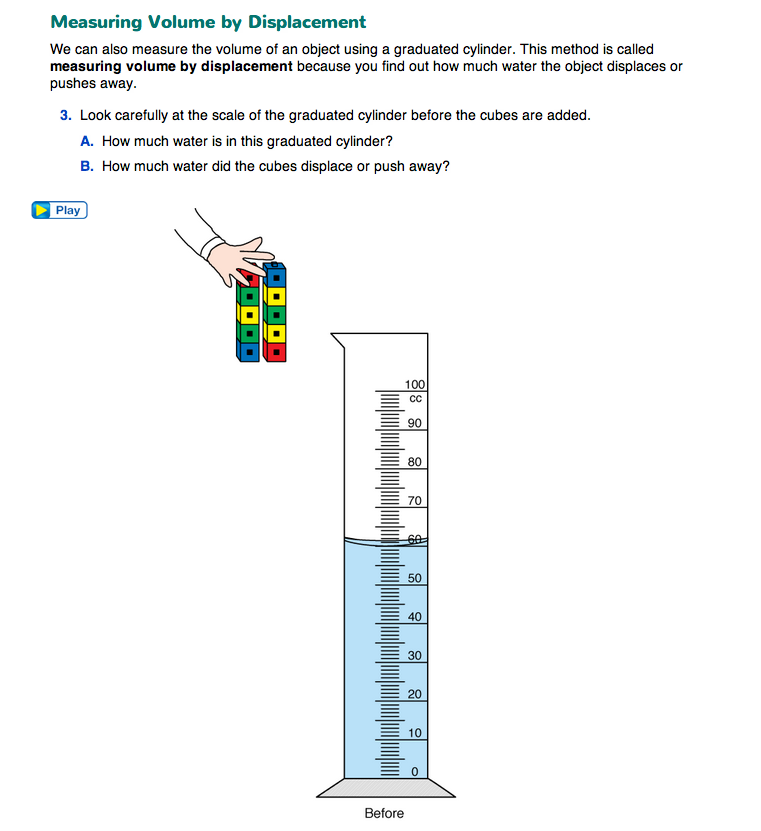
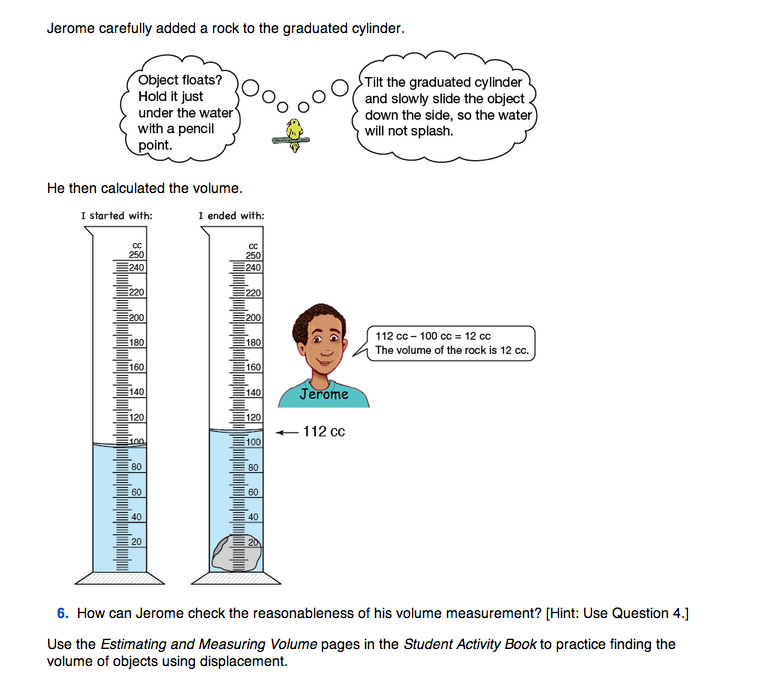
Model How to Measure Volume. Demonstrate how to measure volume by displacement with graduated cylinders using Questions 3–6 in the Student Guide as a reference. Have volunteers model one or more steps for the rest of the class using a graduated cylinder, container of water, eyedropper, and a small object like a rock or a lump of clay.
As students demonstrate, ask:
- How much water is in this graduated cylinder? (Students should look carefully at the scale of the cylinder before the object is added to measure the amount of water.)
- What will happen to the water when we add a [rock or lump of clay]? Why? (The water level in the graduated cylinder will rise because the object has pushed the water away.)
- How can we measure the volume of this object? (We know how much water is in the graduated cylinder before we add the object. We'll find out how much water the object has displaced or pushed away. That will be the volume of the object.)
- What is the volume of [the rock or lump of clay]? Explain how you figured it out. (Students should find the volume of the object by displacement and report its volume in cubic centimeters.)
- What unit do we use when we measure volume? (cubic centimeters or cc)
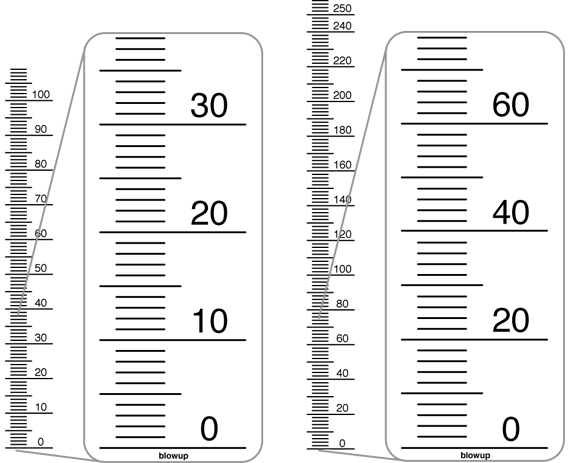
Show the scales on the graduated cylinders in the pictures for Questions 3 and 5 by displaying the 100 cc Graduated Cylinder Scale and 250 cc Graduated Cylinder Scale Masters. See Figure 1.
- Which graduated cylinder has more volume, the 250 cc or the 100 cc cylinder? (250 cc)
- What do you notice about the scale of the 100 cc graduated cylinder? (It is scaled by ones from 0 cc to 100 cc.)
- What do you notice about the scale of the 250 cc graduated cylinder? (It is scaled by twos from 0 cc to 250 cc.)
Display the Reading a Graduated Cylinder Master and the Meniscus Master to illustrate the points in the vignette between Professor Peabody and Jerome before Question 5.
In this vignette, Professor Peabody reminds Jerome to check the water at eye level when reading the scale on the graduated cylinder. When you look at a graduated cylinder from the side, you see the meniscus in a cross section. This causes you to see two lines at the top of the water, not one. The upper line is the ring formed as the top of the liquid creeps up the sides of the cylinder. The lower line is the ring formed at the true level of the liquid. Students should read the lower line when reading the level of liquid in a graduated cylinder.
- What are some important things to remember when we use a graduated cylinder to measure volume by displacement? (Possible responses: Hold the cylinder level. Read the water level at eye level. Read the lower line of the meniscus. Slide objects into the cylinder so that the water doesn't splash out.)