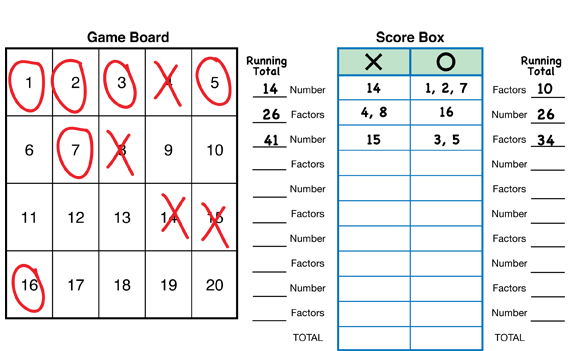Discuss Factors. Begin the lesson by reviewing factors with your students.
- What are all the factors of 6? (The factors of 6 are 1, 2, 3, and 6.)
- What are all the factors of 24? (The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.)
- What are some other numbers that have several factors? (Answers will vary. Examples include 8,
16, and 20.)
- What are all the factors of 13? (The factors of 13 are 1 and 13.)
- What are some other numbers that have only two factors? (2, 3, 5, 7, 11, etc.)
Have students share what they know about factors with a partner. Then have each pair write their ideas on self-adhesive notes. Student might write ideas like the following:
- Factors of a number are numbers you multiply together to get that number.
- Factors are the numbers you multiply together in a multiplication problem.
- 2 and 3 are factors of 6 because you multiply them together to get 6.
- Since 6 is divisible by 3, 3 is a factor of 6.
Ask several students to share their ideas with the class. Ask them to place their completed self-adhesive notes on chart paper that can remain posted in the room. Make sure students remember:
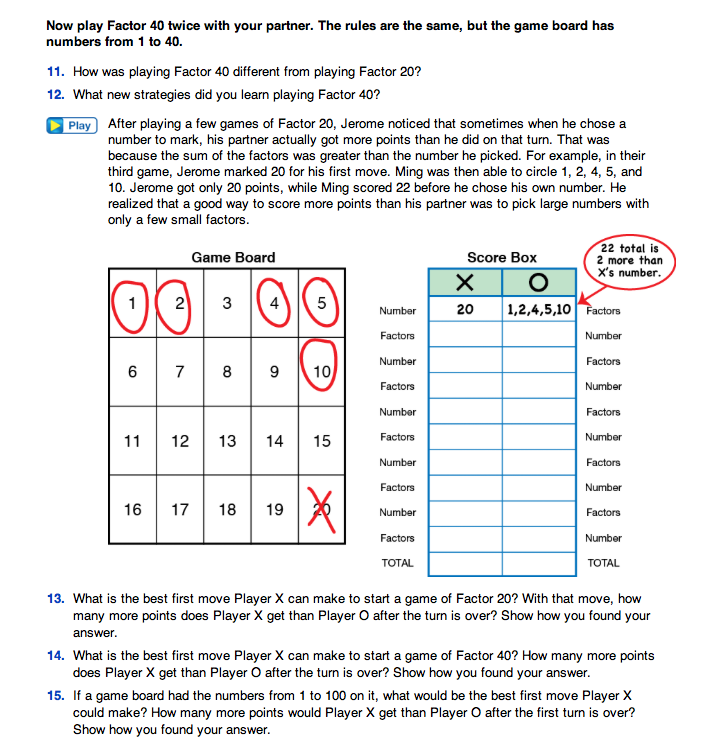
- Factors are numbers that can be multiplied to get a number. That is, the factors of a number are the numbers that divide the number evenly.
- A number that has exactly two whole number factors—one and itself—is called a prime number. If a number has more than 2 different factors, it is a composite number (it is composed of other numbers). By definition, 1 is not a prime number because it has only one factor. Prime numbers will be discussed in Part 2 of the lesson.

Suggestions for addressing possible difficulties with finding all the factors of a number:
Improve understanding of the term factor. Use these prompts:
- Name a factor of 10. Is 2 a factor of 10? How do you know? (2 is a factor of 10 because 2 × 5 = 10.)
- What does that tell you about 5? Is it a factor of 10? (Yes, 2 × 5 = 10.)
- Use your own words as an example to tell me what a factor is. (When you multiply two numbers together, they are factors. So, since 2 × 5 = 10, you know 2 and 5 are factors of 10.)
- Is 10 a factor of 10? How do you know? (Yes, because 10 × 1= 10.)
- Is 3 a factor of 24? How can you find out? (You can skip count by 3s and see if you hit 24.)
- How can you use division to find out? (Try 24 ÷ 3. If it's a whole number, then 3 is a factor. It's like fact families.)
Help students develop a systematic approach. Use the prompts below to help students get started and to make sure they have found all the facts. Finding the factors of 42 is used as an example.
- What number is a factor of every number? (1)
- What do you multiply by 1 to get 42? Write down that multiplication sentence. (42; 1 × 42 = 42)
- You have found two factors. Check for more factors by trying numbers in order. What should we try next? (2; It's even, so if you skip count by 2, you'll hit 42.)
- Write that multiplication sentence. (2 × 21 = 42)
- What 4 factors have we found already? (1, 42, 2, and 21)
- What number is next when we count? How can you check it? (3. I'll try to divide it on my calculator. 42 ÷ 3 = 14. 14 is a whole number, so it is a factor.)
- Write that multiplication sentence and tell me all the factors you have so far. (3 × 14 = 42. I've found 1, 42, 2, 21, 3, and 14.)
- What will you try next? How? (4; 42 ÷ 4 = 10.5. The decimal means it's not a factor.)
- How can you check on 5 as a factor? (42 doesn't end in 5 or 0 like when you skip count, so 5 doesn't work.)
- What is next? (6; 6 × 7 = 42, that's 2 more factors.)
- What number is next? What do you know about it? (7, but I already found 6 × 7.)
Help students organize their work by trying numbers in order and writing down all the number sentences with factors. When a factor repeats, they know they have found them all. Then they can lists all the factors in their number sentences: 1, 42, 2, 21, 3, 14, 6, 7.
Encourage use of calculators and multiplication charts. Encourage students who are still not fluent with the facts to use calculators to check for divisibility and multiplication charts to identify factors. This will allow them to learn the content of the lesson, diminish frustration, and provide contextualized practice with the facts.
Play Factor 20. To introduce the game, show a display of a Factor 20 Game Board and Score Box from the Student Activity Book. Explain to students that they will play a factor game with a partner. Read through the rules of the game on the Factor Games pages in the Student Guide. Using Xs and Os to show each player's moves, mark the game board and score box on the display as if Jerome (Player X) and Ming (Player O) had made the moves described in the Student Guide.
Read the vignette Jerome and Ming Play Factor 20. Have students work with a partner to answer Questions 1–3 in the Student Guide. In Questions 1–3 students determine the result of Jerome and Ming's game moves so far.
Students total their scores after each turn to keep track of who is winning the game. Show how to keep a running score using the score box for Jerome and Ming's game of Factor 20 in the Student Guide. See Figure 1. Suggest that students use mental math to add scores and a calculator to check for accuracy.
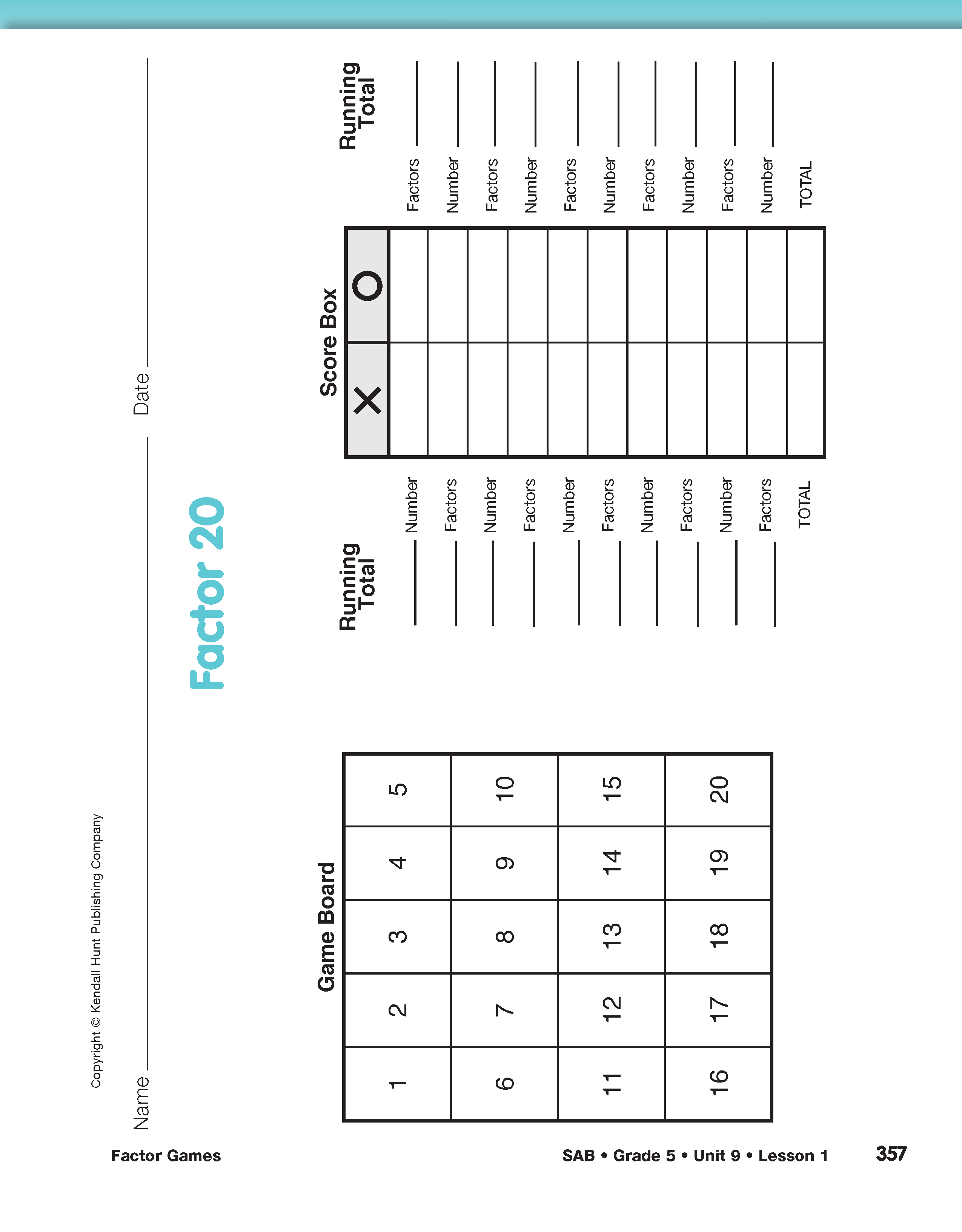
Following the directions for the game in the Student Guide, students are asked to play Factor 20 twice. Partners should alternate using each other's game boards from the Student Activity Book so that each student will have at least one blank Factor 20 Game Board for playing the game at home. They should also alternate which player moves first (i.e., which player uses X and which uses O).
Each pair of students will need one two-sided copy of the Factor 20 page and one two-sided copy of the Factor 40 page from the Student Activity Book. Each student can use half of his or her game boards to play the game in class, and then take the remaining game boards home to play the game with a family member. Combining pages with a partner allows each pair to play four games of Factor 20 and two games of Factor 40 in class. You may want to make additional copies of the game boards.
After playing Factor 20 two times, discuss Questions 4–9 in the Student Guide with the whole class. Write some of the strategies that students share in response to Question 4 on the board or on a display. Students can refer to the strategies on the list when playing Factor 40.
In Question 5, students should identify “good choices” as relatively large numbers such as 19, 17, or 15, that have only a few factors. In response to Question 6, students might say that numbers with several factors, or with relatively large factors, are not good for starting a turn. These types of numbers give more points to the opposing player than numbers with fewer, smaller factors. Numbers such as 12, 18, and 20, for example, are not good choices early in the game when most of their factors are unmarked on the game board.
In Question 7, students describe patterns that occurred in the game. Students might recognize some of the patterns below. They may also find other patterns.
- Numbers with only two factors become against the rules to play as soon as the number 1 is marked.
- Odd numbers typically have fewer factors than even numbers.
- The number 1 is always circled by Player O in the first turn.
- The numbers with the most factors (Question 8) are 12, 18, and 20. Each of these numbers has
six factors, including the number one and the number itself.
- The numbers other than the number one with the fewest factors (Question 9) are 2, 3, 5, 7, 11, 13, 17, and 19. Each of these numbers has only two factors: the number one and the number itself.
Remind students that a number with only two factors—one and the number—is called a prime number. If they found the correct numbers in Question 9, all of the numbers should be prime numbers. In Question 10, students should identify all the nonprime numbers (with the exception of the number 1) as composite numbers.
Playing Factor 40. Now that students have developed strategies and concepts that are useful for playing the game, have them play Factor 40 twice with their partners.

There are three versions of Factor Games in this lesson. Factor 20 and Factor 40 are part of the lesson and include game boards in the Student Activity Book. Factor 100 is not included in the lesson, but it can easily be created using a 100 Chart Master and a blank sheet of paper for keeping score. Several questions in the lesson refer to playing Factor 100 as well, though it is not necessary that students play Factor 100 to answer these questions.
The three versions of the game provide three levels of access to the Factor Games. Students who need more practice finding factors or getting familiar with the rules and strategies of the game can spend more time playing Factor 20.
As skill level increases, students should move to Factor 40 to practice finding factors of larger numbers. If some students are ready to extend their learning, have them play Factor 100.
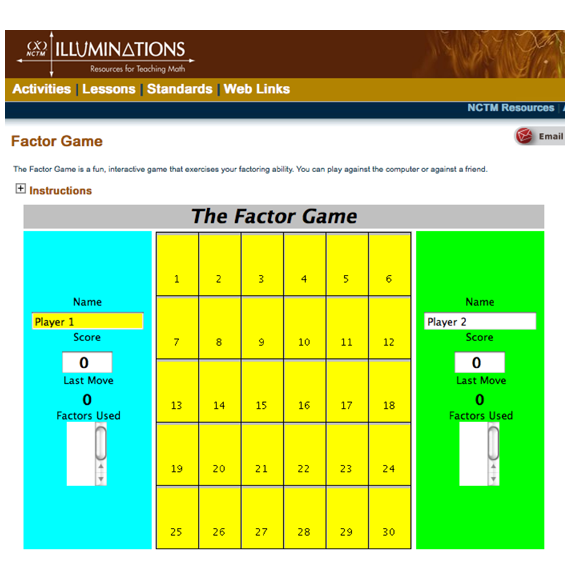
As an alternative to the paper-and-pencil version of the game in this lesson, a computerized version of Factor Games can be found on NCTM's Illuminations website. See Figure 2. The interactive factoring games are similar to those in this lesson, with three game boards varying in difficulty as the number ranges get larger (1–30, 1–49, and 1–100). Students can play against a partner or against the computer. Free access is available for students and teachers at NCTM Illuminations (http://illuminations.nctm.org).
Analyze Moves. After playing Factor 40, have students reflect on their strategies using Questions 11 and 12. Students can begin the discussion with their partners, then share ideas with the whole class.
Read through the next part of the vignette about Jerome and Ming. In Questions 13–15, students work with partners to find the best first moves for games of Factor 20, Factor 40, and Factor 100.
Students may approach these questions in several different ways. Some may methodically find the factors of every number on the board in order to find the best opening move. Others might think about patterns.
As students search for high-scoring opening moves, encourage them to try to solve these problems
more efficiently by asking:
- How did you calculate the difference in points after an opening turn? (Take the number that Player X picks and subtract all of its factors, other than the number itself. For example, the difference in points after choosing 15 is
15 −1 −3 −5 = 6.)
- Which end of the game board did you start with? Why? (Starting with the highest number on the board will produce the high-scoring numbers sooner.)
- Did you check every number when choosing the best first move? When did you realize you could stop checking numbers? (The highest-scoring number will be an odd number, and it will be a prime number. The best first number to choose is always the greatest prime number on the game board.)
- How can you use divisibility rules to solve these problems? (Applying divisibility rules will help find numbers without any factors except for 1 and the number.)
Assign Check-In: Questions 16–19 for students to complete independently. Students analyze the best moves in the Factor 40 game and find numbers with the most factors, numbers that are prime, and the numbers that are composite. Question 16 refers to a game of Factor 40 that Jerome and Ming are playing. Students analyze Jerome's move and try to pick a better move. In Questions 17–19, students find numbers with the most factors, the numbers that are prime, and the numbers that are composite on a blank Factor 40 game board.
Use students' responses to Check-In: Questions 16–19 in the Student Guide to assess students' abilities to find factors for numbers between 1 and 40 [E5]; identify prime and composite numbers [E1]; and find the prime factorization of a number [E6].
Use Factor 20, Factor 40, and Factor 100 games to provide additional targeted practice identifying factors.