Square Number Patterns

Est. Class Sessions: 2

Developing the Lesson

Quadratic Patterns. In this lesson, students explore a type of pattern that is different from the arithmetic patterns in Lesson 3. Students use square-inch tiles to investigate the growth pattern of another animal from Gzorp, the Square Shell Turtle. This animal grows by increasing the size of its square shell each year; therefore, its size increases according to the square of its age in years. This type of pattern is known by mathematicians as a quadratic pattern. Students will see how a pattern based on square numbers grows differently from the arithmetic patterns in Lesson 3. See Figures 2 and 3.

A somewhat surprising mathematical occurrence is that every square number is the sum of consecutive odd numbers. For example, 16 = 1 + 3 + 5 + 7 and 25 = 1 + 3 + 5 + 7 + 9. In this activity, students examine this and related facts about square numbers. It is not as important that students memorize the relationship between square numbers and odd numbers as it is that they experience the process of finding and using patterns.

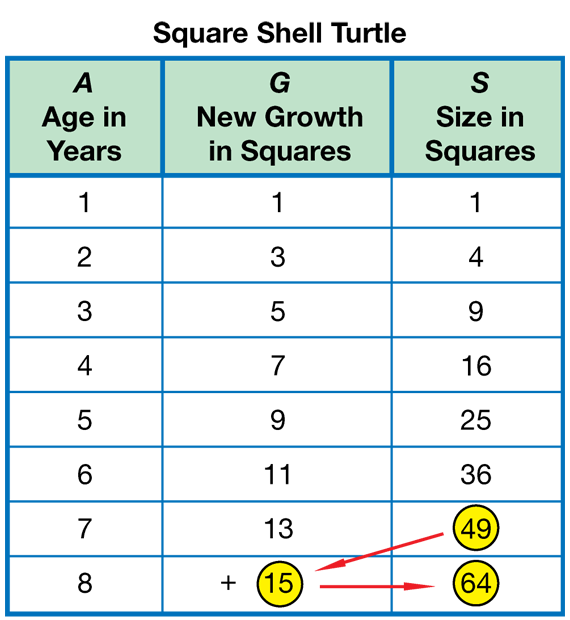
Analyze Square Shell Turtle Pattern. Read the introduction about the Square Shell Turtle on the Square Number Patterns pages in the Student Guide. Working in groups of four, students build the growth pattern as shown and described in the Student Guide. In Question 1, students record data as they add each new color to the pattern up to at least the 8th year of age. A completed data table is shown in Figure 1.

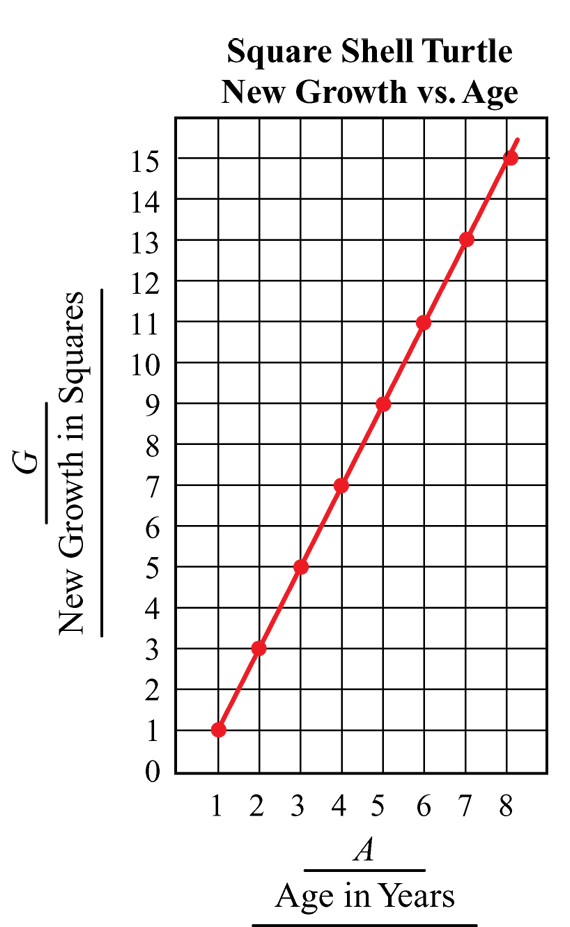
Ask student to work on Question 2 with a partner. Students will need several copies of Half-Centimeter Graph Paper. In Question 2, students draw two separate graphs on Half-Centimeter Graph Paper. For the first graph, Growth (G) vs. Age (A), the points lie on a straight line as shown in the graph in Figure 2. Students draw a line through the points. The question asks students to think about whether the line should pass through the origin.

Ask:

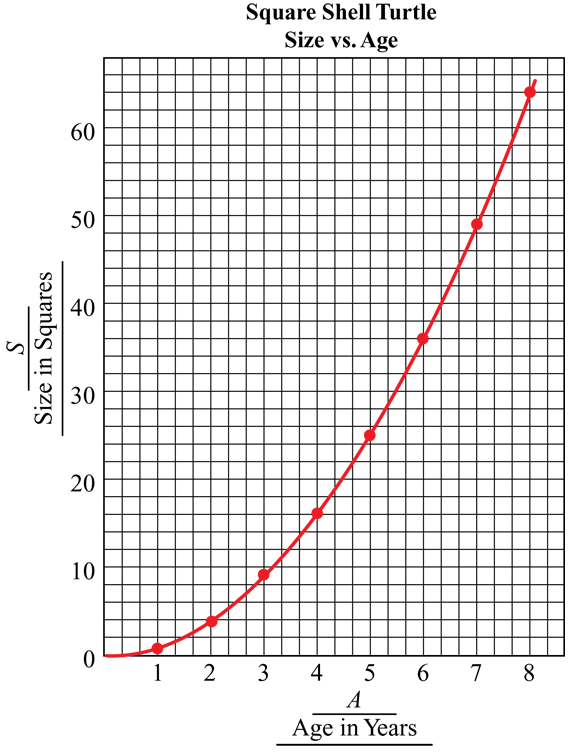
Should your points for the first graph pass through the point (0,0)? (no)
Why or why not? (Answers will vary. Students may see that the line cannot extend through (0, 0) without “bending.” Also, the idea of counting a number of new tiles added to make a turtle that is zero years of age (i.e., with zero squares on each side) does not make sense. Therefore, for this graph the line should not extend to the left of the first data point as shown in Figure 2.)

For Question 2B, students make a second graph, Size (S) vs. Age (A). The points on this graph do not lie on a straight line, making the graph different from many of the other graphs students have seen. See Figure 3. Sometimes when data points from an investigation do not fall on a straight line, we fit a best-fit line to the points, assuming that experimental error is the reason the points aren't exactly on a line. But in this activity, the numbers are exact. Students should draw a curve smoothly through all of the points as shown in Figure 3. Some students may need help doing this since there is often a tendency to “connect the dots” with smaller line segments when the points do not lie on a single straight line.

Ask:

Look at the graph you made in Question 2B. Why do you think we connect the data points with a curved line rather than a best-fit line? (Possible response: The numbers are exact. We are not doing an experiment where numbers could vary in trials, and the points form a curve rather than a line.)
Look at the the two graphs. What is the difference between them? (Possible responses: The graph for Question 2A goes up in a straight line, but the graph for Question 2B has a curved line. The graph for Question 2B also gets much higher in the same amount of years.)

For Question 3 students look at patterns in their data tables.

Ask:

What are some of the patterns you see when you look down the columns?

Record student observations on a display. A list might include the following:

The middle column is a list of odd numbers.
The third column is a list of square numbers.
The number in the third column (S) is the number in the first column (A) multiplied by itself (e.g., 25 = 5 × 5).
The number in the second column (G) is 2 times the number in the first column (A) minus 1 (e.g., 9 = 2 × 5 − 1).
If you subtract a number in the third column from the number below it, you get a number in the second column (e.g., 25 − 16 = 9).

Ask:

What patterns do you see when you look across the rows? (Possible responses: In the same row, the age times itself equals the size. In the same row, A squared is equal to S.)
What patterns do you see when you look both down the columns and across the rows? (Possible responses: You can add 2 to New Growth in any row to find the value in the next row. New Growth goes up by 2 as Age goes up by 1. Age times 2 minus 1 equals New Growth.)

For Question 4, students find the next value of G (new growth in squares) before placing the next set of tiles. Have students propose different rules and post these on a display. Then have other students test the rules.

Ask:

What strategies did you use to find the next value of G (new growth in squares)? (Possible response: I looked down the column and saw that the next value is always two more than the value in the previous row.)

For Question 5, students find how to get the next value of S (size in squares). Have students propose different rules and post these on the display. Then have other students test the rules. See Figure 4 for two possible strategies.

Ask:

What strategy did you use to get the next value of S (size in squares)? (Possible responses: I multiplied the age in years (A) times itself to get the size (S). I found the square of A to get S.)

In Questions 6 and 7, students write formulas for finding the new growth in squares (G) and the size in squares (S) based on the age in years (A). For students who are having difficulty finding formulas, it may be helpful to refer them back to the models they built with tiles and connect them to the numbers in the table.

Ask:

How do the numbers in the second column of your data table (G) relate to the numbers in the first column (G)? (The new growth (G) is always one less than two times the age (A). Therefore, G = 2 × A − 1.)
Look across the rows. How can you use multiplication to find the size of the turtle? (The size S is always A × A or A². For example, the value of S in the 8th row is 8 × 8 = 64 squares. Therefore, S = A².)

In Questions 8–9, students solve problems about the growth of the size of the square shell of the turtle. One of the characteristics of this growth pattern is that the size of the turtle does not grow at a constant rate. It grows 1 square in the first year, then 3 squares in the second, them 5 squares in the third and so on. The ratio of size to age (S/A) changes each year. Therefore, when the turtle is 10 years old, it has far fewer than half of the tiles of a 20-year-old turtle even though 10 is half of 20. This is because 10 × 10 = 100, whereas 20 × 20 = 400. Therefore, only 1/4 of the squares have been placed for a 20 × 20 square when Michael and Ming have a 10 × 10 square done (Question 9).

In Question 10, students make predictions about the growth pattern of the Square Shell Turtle. They use graphs, tables, and formulas to make their predictions.

Student Guide: 438 439 440

Answers