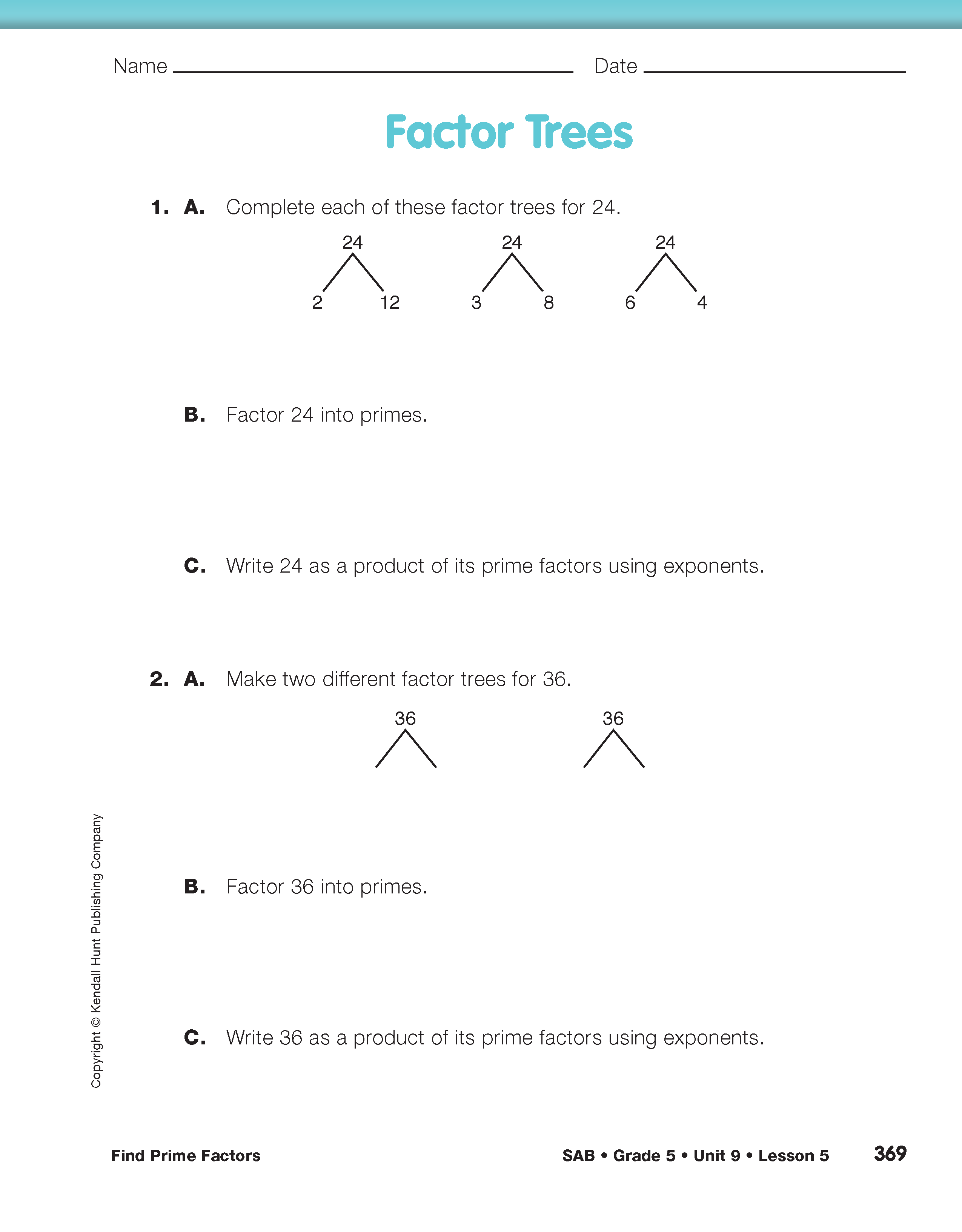
Find Prime Factors
Est. Class Sessions: 1Developing the Lesson
Review Disability Rules. Review divisibility rules with students. Ask students to share some of the divisibility rules they know. Write these rules on a display or chart. See Figure 1 for a sample list.
Then, write these numbers on a display.
| 35 | 584 |
| 4062 | 639 |
| 10,720 | 144 |
Ask students:
Find Factors. Read the challenge that Mr. Moreno made to his class on the Find Prime Factors pages in the Student Guide. Discuss the student responses to this challenge. Students can work in pairs to find the additional information asked for in Questions 1–2. Ask a student pair to come up and share their response on a display or board.
For Question 1, students write 144 as a product of two factors. Collect an organized list of student responses until the class is convinced they have found all the factors. This list represents all the factors of 144.
For Question 2, students write 144 as a product of more than two factors. Discuss and collect student responses to prepare them for finding the prime factorization of a number in Question 3. Possible responses include:
12 × 3 × 4
2 × 9 × 8
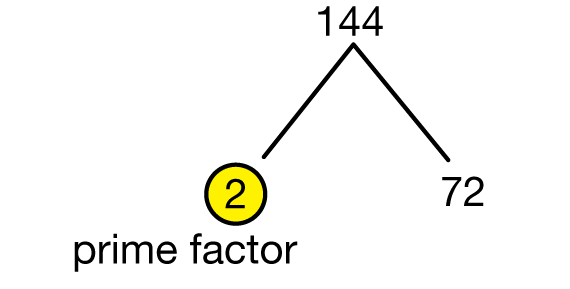
Find Prime Factors. For Question 3, use Brandon's example of finding the prime factors of 144 to review prime factorization and factor trees.
For Question 3A, students practice making a factor tree. One strategy for starting a factor tree is to identify the smallest prime number by which the number is divisible. For example, to find the smallest prime factor of 144, students can use a calculator or divisibility rules. Students should be able to identify this number as 2. Once they have identified this prime factor, they can then use their calculators or other methods to divide 144 by 2 and find the other number in this factor pair: in this case, 72. Students can record this pair of factors in their factor trees for 144. See Figure 2.
Students can now continue their factor trees by finding a pair of factors for 72. Have students complete the factor tree for 144. One possible tree is shown in Figure 3.
After completing Question 3B, students should realize that even though there may be many different ways to make a factor tree for a number, they will always end up with the same prime factors (though they may be in a different order).
Once students have made factor trees, they can write numbers as products of their prime factors. This is called prime factorization. Students make a factor tree and write a prime factorization using exponents in Question 4. You may need to review exponents with students.
Have students complete the Factor Trees page in the Student Activity Book for additional practice.
Exponent Key. For Questions 5–6, students use the exponent key on a scientific calculator. Students can use this key to check their prime factorizations written with exponents. Exponent keys are labeled differently on different scientific calculators. Possible labels include:
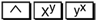
Help students identify the exponent key on their calculators.
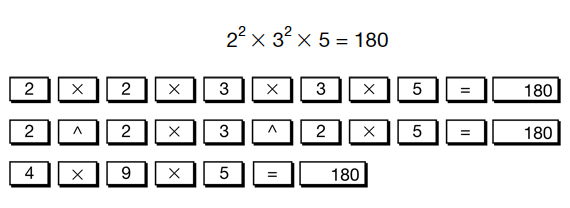
Collect student responses to Question 6. See Figure 4 for a collection of ways students can use the calculator to check the prime factorization. Notice that in the last example students solved some of the problem in their heads and then used the calculator to finish the problem.
In Question 7, students finish the prime factorization of 120. Maya and Nicholas have started to find the prime factorization of 120 differently. Students are asked to complete the prime factorization.
Ask:
For Questions 8 and 9, students check to verify that a prime factorization was found. In both of these problems, one of the primes is close to or over 100. Use Question 9 to challenge students to determine if a number larger than 100 is prime. Encourage students to use the divisibility rules or to check the divisibility of the number using other prime numbers.
Assign Check-In: Question 10 in the Student Guide for students to complete independently.