Lesson 1

Measuring Volume

Est. Class Sessions: 1–2

Daily Practice and Problems

Teacher Notes
X

TIMS Challenge

This problem can serve as a Problem of the Week.


  2. The shape number goes up by one. The area goes up by 4 sq. cm. All of the areas are odd numbers.
  3. Shape 10 has an area of 41 sq. cm. Student strategies for finding the area of Shape 10 will vary. Since students see that the area increases by 4 sq. cm for each new shape they may add to the data table and use that pattern to build the table to include Shape 10. An alternative strategy is to find how the shape grows. A possible response: I noticed that the area for each shape was 4 times the shape number plus 1 square centimeter for the one in the middle of the shape. So I figured out that 10 × 4 + 1 = 41. I also saw that each side of the shape had the same number of square centimeters as the shape number and then there was one square in the middle. Since there are 4 sides to the shape I knew that Shape 10 would have 10 + 10 + 10 + 10 for the sides, or 40 sq. cm for the legs and then 1 more sq. cm for the middle, or 40 + 1. That made a total area of 41 sq. cm for Shape 10.
  4. The area for Shape 50 will be 201 sq. cm. Student strategies may vary. Some students may continue the data table or they may find the area of the shape using the rule 4N + 1 = A or 50 × 4 + 1 = 201.
  5. Using words: To find the area multiply the number of the shape by four and add 1. Using symbols: 4N + 1 = A.
  6. 4 × 75 + 1 = 301 sq. cm

B. Find the Pattern

You will need one or two sheets of Centimeter Grid Paper for these problems.

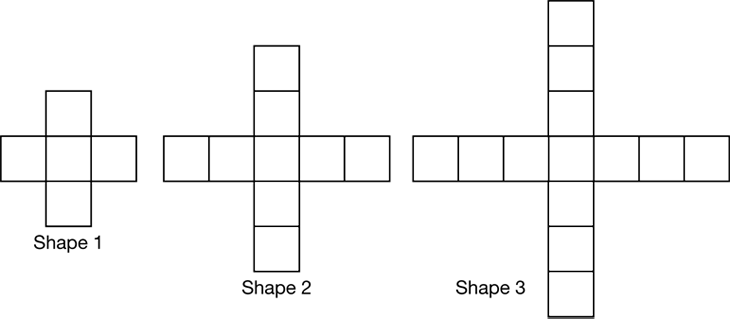
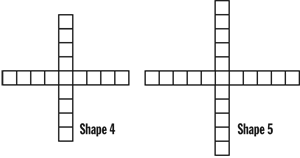
  1. Draw Shapes 4 and 5 on Centimeter Grid Paper.
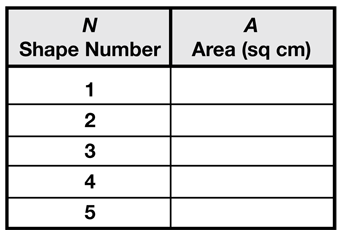
  2. Complete the data table for Shapes 1–5. What patterns do you see?
  3. Find the area of Shape 10. Show or tell how you found your answer.
  4. Predict the area of Shape 50. Show or tell how you made your prediction.
  5. Write a rule for finding the Area (A) of a Shape if you know the Shape Number (N).
  6. Use your rule to find the Area of Shape Number 75.