What Is in That Pocket?

Est. Class Sessions: 3

Developing the Lesson

Partition Ten into Two Parts. Display the Two Pockets Work Mat from the Student Activity Book. Distribute 10 pennies to each student. Tell students they are going to put their ten pennies into two pockets on their Two Pockets Work Mat in the Student Activity Book. See TIMS Tip. Place six pennies in the top pocket and four pennies in the bottom pocket as an example.

Ask:

How many pennies are in the top pocket? (6)
How many pennies are in the bottom pocket? (4)
What number sentence can I write to describe my pennies? (6 + 4 = 10)
Is this the only way I can arrange the ten pennies in my two pockets? Show me another way.

To help keep pennies in place, have students take the Two Pockets Work Mat out of their Student Activity Book so it will lie flat on their work surfaces.

Encourage students to show other ways to arrange the pennies and write corresponding number sentences. Since there is more than one way to solve this problem, tell them they will keep track of all the different ways on the Pockets and Ten Frames pages in the Student Activity Book. They will record the different solutions on ten frames and in number sentences as shown in the example.

Ask a student to display and share his or her solution. Students should record the solutions at their desks to practice filling in the ten frames.

Ask:

Is this a different way to arrange the pennies into the two pockets?

Come to an agreement that reversing the order of the pennies in the pockets (e.g., four pennies in the top and six in the bottom versus six pennies in the top and four in the bottom) creates two different solutions.

Ask:

What happens to the total number of pennies when the numbers of pennies are turned around? (The total is the same.)

Find How Many Ways. Have students work in pairs to find as many different ways as they can to arrange the ten pennies in the pockets and to record their solutions on the Pockets and Ten Frames pages. Students should follow the example and place Xs in the ten frame to represent the pennies in the top pocket and dots to represent those in the bottom pocket. When appropriate, challenge student pairs to see if they have all the possibilities. If necessary, remind students that putting zero pennies in the top pocket or zero pennies in the bottom pocket is a possibility.

Bring the class together and ask student pairs to share their solutions. Ask one student in the pair to place pennies in the pockets on the display and record their solution on a ten frame and in a number sentence. As each solution is presented, display the completed ten frame and number sentence in a place students can continue to review them as other combinations are shared. See the TIMS Tip. Before adding the ten frame to the display, ask students if the solution is a new arrangement and if the number sentence represents the arrangement.

Ask:

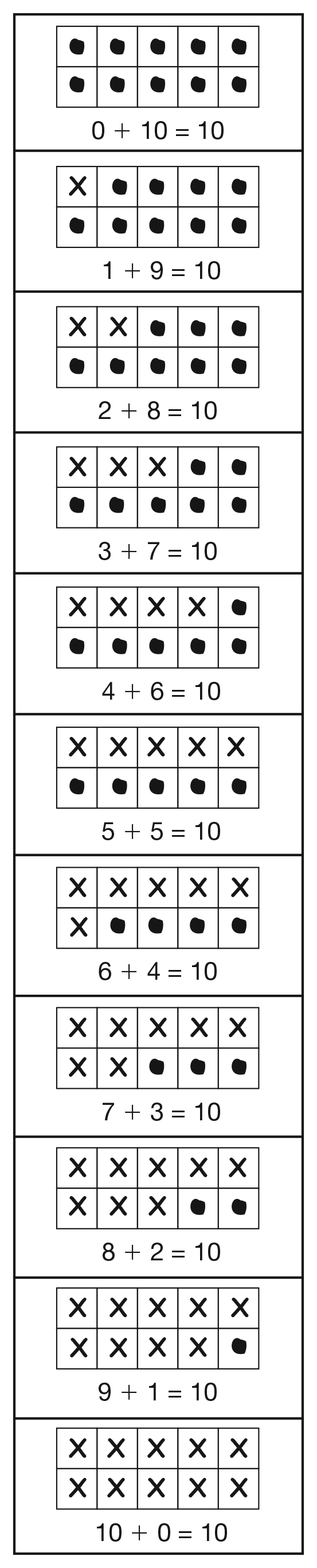
Is this a different solution from any that are already posted? Is this a different ten frame and a different number sentence? Tell me how you know. (Possible responses: It is already up on the board. See we already have a ten frame with just four Xs. Or, it is already there. It is 4 + 6 = 10 and John put up 4 + 6 = 10 for the first one.)

If it is a new solution, then post it with the other ten frames and number sentences. If it is a duplicate, post it in a different place labeled "Repeats." See Figure 1 for a collection of ten frames showing how a group of students organized the ten pennies. Note that 5 pennies in each pocket is missing from their collection. Also see the Sample Dialog.

Display Arrangements of 10 pennies. Use the copies of the Ten Frames and Number Sentences Master you prepared to display each combination. Have students prepare to share their solution on one of these copies. If the combination is new, tape the ten frame and number sentence copy to the
"10 pennies" chart you prepared. If the combination is a repeat, tape the ten frame and number sentence copy to the "Repeat" chart you prepared. See Materials Preparation.

Several copies of the second page of the Pockets and Ten Frames pages in the Student Activity Book can also be used to display ways to arrange the 10 pennies. Choose a way to indicate which arrangements are new arrangements and which combinations are repeat arrangements.

The Two Pockets and Ten Pennies Table Master can also be displayed to collect the penny arrangements. One copy can be used during the initial collection and another can be used to rearrange the data to be sure all the combinations have been found. This table should supplement the display of the ten frames as the quantitative representation better supports students' reasoning.

Use this dialog to discuss ways to arrange

ten pennies into two pockets.

Teacher: Can anyone find a combination that is missing? Talk with your partner.

Ana: Jackie and I thought of 9 + 1 = 10.

Teacher: Is 9 + 1 = 10 a different solution than those on the board? [The class agrees that it is.] How did you figure that out?

Ana: We saw 1 + 9 = 10, but 9 + 1 wasn't there.

Teacher: What makes 9 + 1 and 1 + 9 different?

Ana: Ours has one dot, but 1 + 9 has nine dots.

Teacher: The ten frames do look different. You saw that you can turn the numbers around. The one on the board has nine Xs and one dot, but the ten frame Ana is describing has one X and nine dots. Ana, please make that ten frame and put it on the board next to the one with nine Xs and one dot. Jackie, record the information in our table. Can someone find another missing combination?

Nicholas: How about 10 + 0?

Teacher: How did you think of that?

Nicholas: When we did the pocket parts, sometimes a pocket had zero pennies.

Teacher: What will that ten frame look like?

Nicholas: 10 Xs and no dots.

Teacher: What is the number sentence?

Luis: 10 + 0 = 10. And turn it around
0 + 10 = 10.

Teacher: Good thinking. [The students post the strips and record information in the table. At this point, the class has filled in
10 ten frames and has found all but one solution as shown in Figure 1.] Is there another missing combination?

Maya: There aren't any.

Teacher: How can we tell if there are more missing combinations?

Linda: Well… we can't think of any more.

Teacher: How can we be sure that we have all of the combinations?

Linda: We have to check them.

Teacher: Explain what you mean by checking.

Linda: I think we have to try the numbers in the top.

Teacher: What numbers do you want to try?

Linda: The ones we used, you know – one, two, three, four, five, six, seven, eight, nine, ten.

Luis: We forgot zero again.

Teacher: If I start with zero pennies in the top pocket and ten pennies in the bottom, do I have that combination already? [The teacher places ten pennies in the bottom pocket.]

Luis: We just put that one up and its turn around. [The teacher moves the ten frame showing 0 + 10 = 10 to a place where she can make a new column as the class checks their work.] Over here we can keep track of the ones we know we have tried. Where is this one in our table? [Luis points to the table entry.]

Teacher: Now, using Linda's strategy, I will put one penny in the top pocket and nine in the bottom and see if we have the combinations. [The teacher repeats the process with one, two, three, and four pennies and continues moving the strips into a column creating a visual pattern as in Figure 2. The combination with five pennies in each pocket is missing. The teacher places five pennies in the top pocket and five in the bottom.] Do we have this combination already?

Romesh: No.

Teacher: Describe the ten frame that matches.

Romesh: It would be five and five.

Teacher: What do you mean, "five and five"?

Romesh: Five Xs on top and five dots on the bottom.

Teacher: Great. Let's make a strip and add that solution to the table. [The class continues the process until they have arranged all the strips as show in Figure 2.]

Decide if all arrangements were found.

After students share their solutions, present this challenge:

Do we have all the possible ways to arrange ten pennies into two pockets?

Use the Sample Dialog to discuss ways to arrange ten pennies into two pockets. The dialog discusses the use of ten frames and patterns to find all solutions. Note that students agreed turn-around facts are different responses, recognized that zero is a partition of ten, and found an efficient strategy to organize information to determine whether all partitions have been found.

There are eleven possible solutions as shown in Figure 2. Use a display of the Two Pockets and Ten Pennies Table Master to reorganize the penny arrangements to help students decide if they have found all the possible arrangements. See Figure 3.

Referring to the ten frames, ask:

What patterns do you see in the ten frames and number sentences? (Possible responses include:
The way you put the pennies shows on the board. First there are all dots and no Xs, then one X, then two Xs. It keeps going like that; The number of Xs gets one bigger each time and the number of dots gets smaller; The numbers in the number sentences match the Xs and dots. The first number gets one larger and the second number gets one smaller; The first five number sentences are the turn-around sentences for the bottom five sentences.)