Pennies, Pockets, and Parts
Developing Number Concepts
"Children who understand the big ideas of composition and decomposition are more likely to invent reasoning strategies, such as translating combinations into … read more
Developing Number Concepts
"Children who understand the big ideas of composition and decomposition are more likely to invent reasoning strategies, such as translating combinations into easier or known expressions" (Baroody, 2006). Students extend their work with numbers to partitioning numbers, i.e., identifying parts of a whole. They learn, for example, that ten is five plus five, four plus six, three plus seven, and so on. The concept of the part-whole relationship helps children develop more mature number sense, a better understanding of addition and subtraction, and strategies for the basic facts. Although students will be working informally with addition and subtraction concepts, do not focus on the operations or on computation.
Ten frames, which are introduced in this unit, are frequently recommended for primary grade mathematics instruction (Thompson, 1990; Thornton, 1990). Ten frames foster mental imagery based on the important benchmarks of five and ten that can help students build understanding of basic number concepts. Work with ten frames also provides a foundation for later developing fluency with the addition and subtraction math facts.
To develop these basic number concepts, students represent them using ten frames, a part-part-whole model, and number sentences. To further develop understanding, they connect these representations to more familiar ones, including number lines and connecting cubes. See Figure 1.
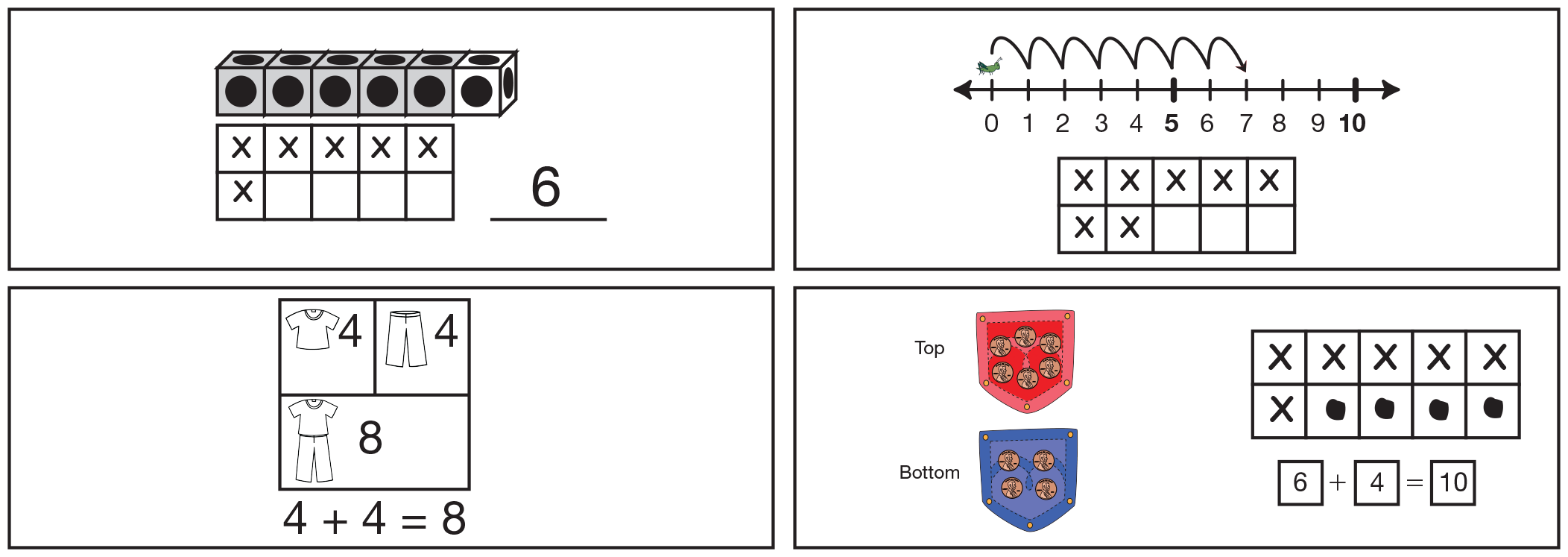
Figure 1: Connecting representations of numbers
Research supports an approach to learning the
facts that emphasizes the use of strategies to find
answers over rote memorization of facts. As stated
in Mathematics for the Young Child, "Encouraging
children to use efficient strategies to derive
unknown facts before drill is better than 'premature
drill' and doing so increases both initial learning
and retention" (Thornton, 1990).
Learning through Problem Solving
"Solving problems is not only a goal of learning mathematics but also a major means of doing so. Problem solving is an integral part of all mathematics learning, and so … read more
Learning through Problem Solving
"Solving problems is not only a goal of learning mathematics but also a major means of doing so. … Problem solving is an integral part of all mathematics learning, and so it should not be an isolated part of the mathematics program" (NCTM, 2000). In this unit, data collection and analysis provide rich contexts and concrete models to support students' problem solving and reasoning. There is evidence that young children bring to school a wealth of informal mathematical knowledge and strong problem-solving capabilities. This suggests that children are able to solve many kinds of problems in familiar contexts, particularly when they can use manipulatives, drawings, and their own ways of thinking.
"When the teaching and learning of mathematics is approached from a problem-solving perspective, concepts and procedural skills are developed on the basis of problem settings that require those concepts and skills. A problem-solving approach helps young children make sense of the concepts, skills, and relationships that are essential in an early childhood mathematics curriculum" (Worth, 1990).
It is important that students encounter a range of different kinds of problems. The work of Thomas Carpenter and his colleagues (Carpenter, Fennema, and Peterson, 1987; Carpenter, Carey, and Kouba, 1990) with the Cognitively Guided Instruction Project (CGI) provides insights that can help teachers with this process. They devised a classification scheme for problems most adults would solve by addition, subtraction, multiplication, or division. CGI classifies the addition and subtraction situations into 11 types of problems. Research by the CGI Project and others has shown that certain types of problems are more challenging than others. Traditionally, just two of the 11 addition and subtraction types have dominated elementary mathematics textbooks in the United States. Moreover, these favored problem types are the easiest to solve.
Most of the addition problems that elementary students encounter are classified as "join—result unknown." (For example, there are three corn plants in one row and two plants in another row. How many plants are there?) Similarly, most of the subtraction problems are "separate—result unknown." (For example, a farmer had 8 carrots and a rabbit ate 6 of them. How many carrots did the farmer have left?) With such a limited variety of problems, students develop a limited conception of addition and subtraction.
In this unit students will focus on problems from four basic types:
Join – Result Unknown
Levi wants to buy a sticker and a pencil. How many
pennies does he need?
Separate
Sam has 7¢. He wants to buy a pencil. How much
money will he have left?
Comparison
How much more is an eraser than a pencil?
Join – Change Unknown
Linda has saved 6¢. She wants to buy an eraser.
How many pennies does she still need to save?
Children must be allowed sufficient time to solve problems in their own ways. They need to be able to support their thinking with a variety of tools and be encouraged to find a variety of solution strategies. The opportunity to share mathematical thinking is crucial in creating a classroom climate in which children explore, share, and think critically about their problem-solving strategies and those of others.
As stated in the Math Practices of the Common Core Standards for Mathematics, "Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments."
Teaching about problem solving is part of the instructional fabric of Math Trailblazers. Students engage in problems or tasks that promote a productive struggle and are used to promote conceptual development. The Math Practices page in the Student Activity Book Reference section and shown in Figure 2 provides a framework to focus discussions and make the problem-solving process explicit.

Figure 2: Math Practices
Here is an example of two different approaches to solving a problem.
| Problem: | Melinda has five pennies and Carlos has four pennies. How many do they have together? |
| Child A: | Child A builds a train of five cubes and a train of four cubes and puts them together. He says,
"I counted five, six, seven, eight, nine." |
| Child B: | Child B places five pennies on a ten frame in the top row, then adds four pennies to the bottom row. She explains, "I see that there is one square with none. So that is one less than ten, or nine." |
It is important to nurture children's abilities and interest in problem solving, both by posing problems and by
allowing them to create and solve their own problems.
Resources
- Baroody, A.J. "Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them." In Teaching Children Mathematics, 13 (1), pp. 22–31. National Council of Teachers of Mathematics, Reston, VA, 2006.
- Bennett, A.B., Jr., and L.T. Nelson. Mathematics for Elementary Teachers: A Conceptual Approach 5th Edition. McGraw Hill, Boston, 2001.
- Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically: Integrating Arithmetic & Algebra in Elementary School. Heinemann, Portsmouth, NH, 2003.
- Carpenter, T.P., D.A. Carey, and V.L. Kouba. "A Problem-Solving Approach to the Operations." In Mathematics for the Young Child, J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH, 1999.
- Carpenter, T.P., E. Fennema, and P. Peterson. "Cognitively Guided Instruction: The Application of Cognitive and Instructional Science to Mathematics Curriculum Development." In Developments in School Mathematics Education around the World: Applications-Oriented Curricula and Technology-Supported Learning for All Students. I. Wirszup and R. Streit, eds. National Council of Teachers of Mathematics, Reston, VA, 1987.
- Carpenter, T.P., and J.M. Moser. "The Acquisition of Addition and Subtraction Concepts in Grades One through Three." In Journal for Research in Mathematics Education, 15 (3). National Council of Teachers of Mathematics, Reston, VA, 1984.
- Council of Chief State School Officers. Common Core State Standards for Mathematics, 2010.
- National Research Council. "Developing Proficiency with Whole Numbers." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Research Council. "Teaching for Mathematical Proficiency." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Thompson, C.S. "Place Value and Larger Numbers." In Mathematics for the Young Child. J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Thornton, C.A. "Strategies for the Basic Facts." In Mathematics for the Young Child. J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Van De Walle, J.A., K.S. Karp, and J.M. Bay-Williams, "Developing Early Number Concepts and Number Sense." In Elementary and Middle School Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc. Upper Saddle River,
NJ, 2013. - Worth, Joan. "Developing Problem-Solving Abilities and Attitudes." In Mathematics for the Young Child, J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.












