Lesson 7

Purchasing with Pennies

Est. Class Sessions: 2

Developing the Lesson

X

Four basic types of problems will be used in this activity:

1. Join – Result Unknown
Leticia wants to buy a sticker and a pencil. How many pennies does she need?

2. Separate
Carlos has 7¢. He wants to buy a pencil. How much money will he have left?

3. Comparison
How much more is an eraser than a pencil?

Join – Change Unknown
Phyllis has 3¢. She wants to buy an eraser. How many pennies should she borrow from a friend?

See the Mathematics in this Unit for more information.

Refer students to the display of the "store" items. See Materials Preparation. Distribute pennies, connecting cubes, and a copy of the Two Ten Frames Master. Display the Math Practices page from the Student Activity Book Reference section.

Pose a "join" problem similar to the following:

X
  • Sam wants to buy a sticker and a pencil. How many pennies does he need?

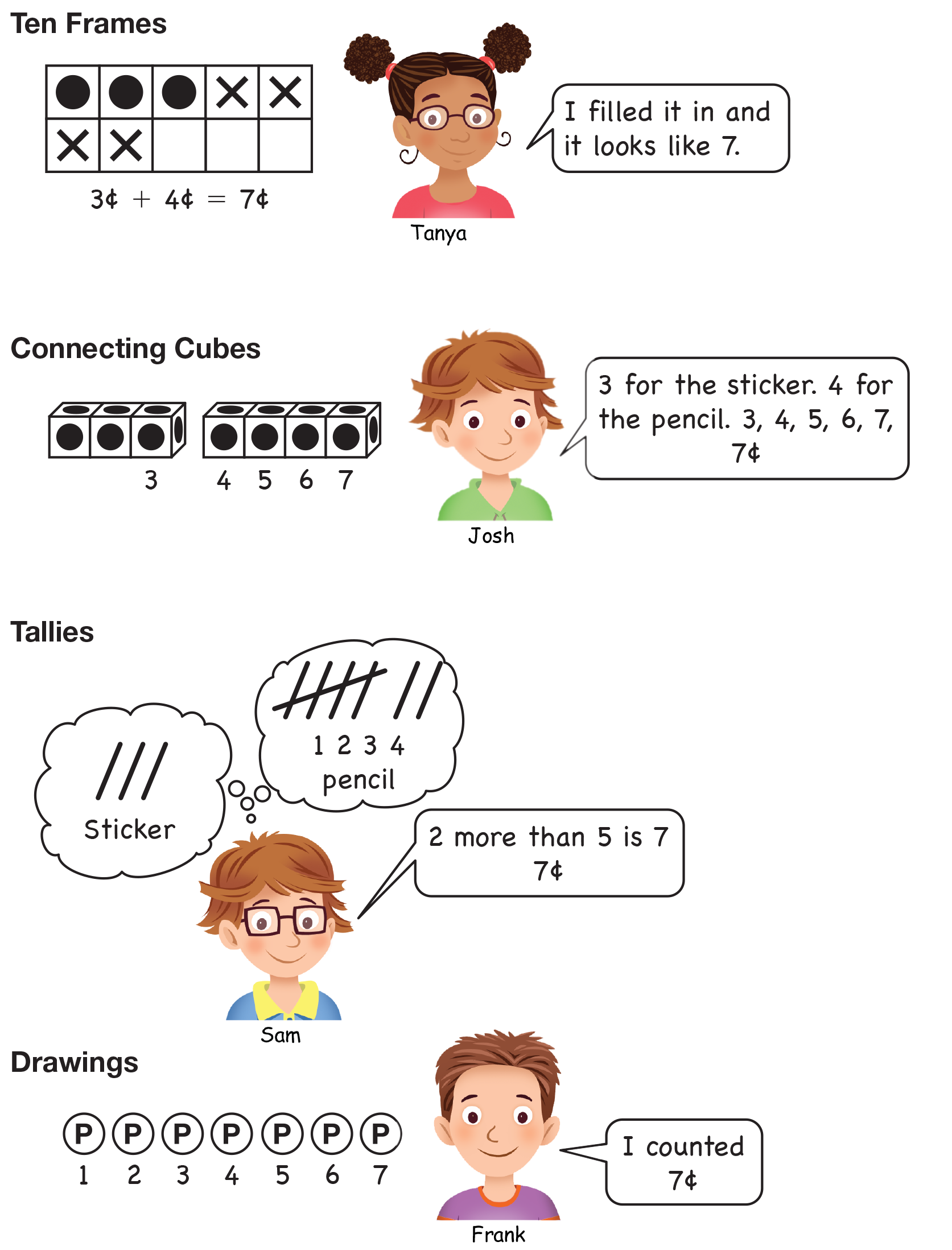
Ask students to solve this problem encouraging them to use the tools you have provided and used in this unit. After students have had a few minutes to solve the problem, refer to Math Practices 2 and 5, Find a strategy and Show my work, on the Math Practices page and ask students to show their partner how they solved Sam's problem. Circulate among the students listening for a variety of solutions to share with the class.

Ask:

X
  • What are some of the tools you used to solve Sam's problem? (Possible responses: ten frames and pennies, tallies, connecting cubes, fingers, a drawing.)
  • Who would like to show how to solve Sam's problem with [tools]? (See Figure 2 for some possible tools and strategies.)

While students are sharing their solution strategies, listen for students who are using a counting-all strategy rather than counting on. Encourage these students to start with a number in the problem and count on, if appropriate. Frank's solution in Figure 2 shows a student counting all. The other students in the Figure are either using benchmarks to find the sum or using a counting-on strategy. See the Sample Dialog.

X

Use the Sample Dialog to guide a discussion of solutions to different types of problems. The discussion refers to the items shown in Figure 1.

Teacher: You have 10¢. Can you buy a ball and a crayon? Work a minute with your partner. Be ready to explain how you solve the problem. …Michael, what did you and Jerome decide?

Michael: We have enough.

Teacher: How did you decide?

Jerome: We put two pennies and seven pennies on a ten frame and there was one box left over.

Teacher: So you would have one penny left from your ten cents. Did anyone solve it a different way?

Irma: You can see it on the number line.

Teacher: What did you and Grace see?

Irma: We hopped two then we hopped seven and we landed on nine. We were one away from ten.

Teacher: Did you and Irma get the same answer as Michael and Jerome doing it a different way?

Grace: Yes. They both had one left.

Teacher: Tell me what you mean? What did they have left?

Grace: Jerome had one box left on the ten frame and we had one hop left.

Teacher: So, we agree that they would have one cent left after they bought the ball and crayon. Michael and Jerome showed it with one empty box in the ten frame and Irma and Grace showed it with one more unit to go to get to ten on the number line.

Teacher: Did anyone use connecting cubes or tally marks? If so, how?

Mark: I used tally marks. I marked seven with a five group with the slant line and two more. Then I added two more lines for the crayon. I knew it was OK because ten cents would be two five groups with slant lines. My tally marks are less—I need one more to get the second slant line.

Teacher: You're saying you compared your tally marks to ten tallies and saw that you had less than ten, so you knew you had enough to buy both items. Good thinking. Did anyone else have another method?

Sue: I used a number line like Irma, but I did it differently. I started on seven because it was the biggest number then just added on the two for the crayon.

Teacher: Good, Sue. You used the counting-on strategy and explained it well.

X

Changing the price tags to larger numbers may be appropriate for individuals who are ready to solve problems with numbers to 20.

Give students more problems to solve, perhaps trying different types of problems. See the Content Note. When appropriate, ask students to represent their solution with number sentences.

Here are some sample problems:

X
  • Roberto wants to buy an eraser and a ball. How many pennies does he need?
  • Linda has 5¢. She wants to buy a sticker. How much money will she have left?
  • Nila has 3¢. She wants to buy a pencil. How many pennies does she need to borrow?
  • You have 10¢. Can you buy a pencil and an eraser? How much money will you have left over?
  • You bought two things and spent 7¢. What did you buy? See if you can find more than one answer.
  • You have 9¢. How many crayons can you buy? How many erasers? pencils? stickers?
  • You have 10¢. If you buy two crayons and one eraser, how much money will you have left over?
  • You have 9¢. You want to buy a pencil and a sticker. Can you buy anything else?
  • You have 10¢. Can you buy a ball and a pencil?
  • How much more is a ball than a crayon?

Students will solve similar problems throughout the year in the Daily Practice and Problems.

X

Observe students' abilities to represent addition situations with drawings, ten frames, counters, and number lines [E6] and solve addition word problems using a ten frame [E7] while students are solving problems involving pennies. You also have the opportunity to assess students' abilities to find an efficient strategy [MPE2] and show or tell their work [MPE5].

Adventure Book:
Student Activity Book:
Master:
Items with price tags
X
+
Some strategies for solving 3¢ + 4¢ = 7¢
X
+