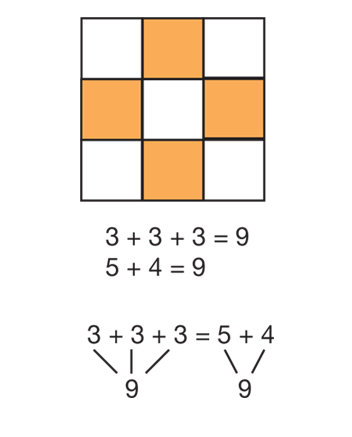Number Sentences for Tile Designs

Est. Class Sessions: 2

Developing the Lesson

Part 1: Number Sentences for Tile Designs

Equal Sign. The equal sign in mathematics expresses a relationship of equivalence between the two sides of an equation or number sentence. Young students, however, frequently see the equal sign as an indicator that “the answer comes next,” or “now solve the problem.” This misperception may create difficulty when a student reaches algebra. Throughout Math Trailblazers, students encounter number sentences written with the solution both first and last, such as 11 = 6 + 5 and 6 + 5 = 11. In this lesson, students are introduced to number sentences in which both sides of the equal sign have more than one number, such as 7 + 4 = 6 + 5.

Students write different number sentences to describe the same tile design, for example 3 + 2 + 1 = 6 and 4 + 2 = 6. See the second design in Figure 1. From there, it is a natural extension to observe the relationship between the two number sentences, 3 + 2 + 1 = 4 + 2. When confronted with the question of whether such a statement is true or false, students at first may need to find the value of the expression on each side of the equal sign to answer the question. With experience, students will develop the ability to reason from examining the two sides. For example, a student may reason, “I know that 3 + 2 + 1 = 4 + 2 because I can add the 3 and the 1 to make 4 on the left side and that makes the two sides the same, 4 + 2.” Using the equal sign flexibly will allow students to represent their thinking more easily, such as knowing that 19 + 4 is 23 because 19 + 4 = 20 + 3.

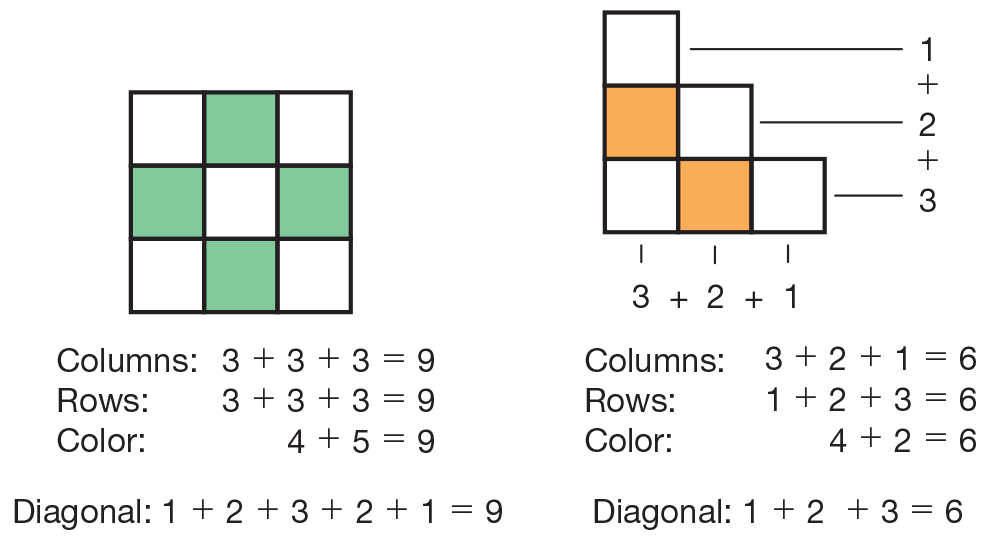
Write Number Sentences. Display the square design (3 x 3) shown in Figure 1 that you prepared. See Materials Preparation. Using the tile design, show that the horizontal line of tiles is a row and the vertical line of tiles is a column. Ask students to tell you what the total number of tiles is. Then show the number sentence 3 + 3 + 3 = 9. Ask questions similar to the following as you point out the appropriate sections of the design.

Ask:

How does this number sentence fit the design? What do you think this number sentence says about how the tiles were counted? (There are 3 rows of 3 tiles and there are 3 columns of 3 tiles. They counted by rows or by columns.)
Did anyone count the tiles by color (white and gray)? What number sentence describes that way to count? (5 + 4 = 9)

Show or have a student show the diagonal lines of tiles on the design.

Explain what diagonal means and ask:

What if we counted by diagonals? What would that number sentence be? (1 + 2 + 3 + 2 + 1 = 9)
Would 6 + 2 fit this design? Why or why not? (Possible response: No, 6 + 2 = 8 and there are 9 tiles. There is no 6 in either a row or column and there are not 6 of either color. )

Show the second tile design in Figure 1. As you discuss each of the number sentences, have a student point out the part of the design that corresponds to each addend in the number sentence.

Ask:

What are different ways we can count the tiles in this design? (color, row, column, diagonal)
If we count by rows, what number sentence describes the design? (3 + 2 + 1 = 6 or 1 + 2 + 3 = 6)
If we count by columns, what number sentence describes it? (3 + 2 + 1 = 6 or 1 + 2 + 3 = 6)
If we count by colors? (4 + 2 = 6 or 2 + 4 = 6)
If we count by diagonals? (3 + 2 + 1 = 6 or
1 + 2 + 3 = 6)

Area. Counting the total number of tiles doubles as an exercise for finding the area of the shape. Since the tiles are square-inch tiles, the number of tiles is the same as the area in square inches. If students make different shapes but have the same number of tiles, the areas of their shapes will all be the same. Remind students of the finding area work they did in Grade 1 Unit 8 Counting and Adding to Measure Area and point out that different shapes can have the same area.

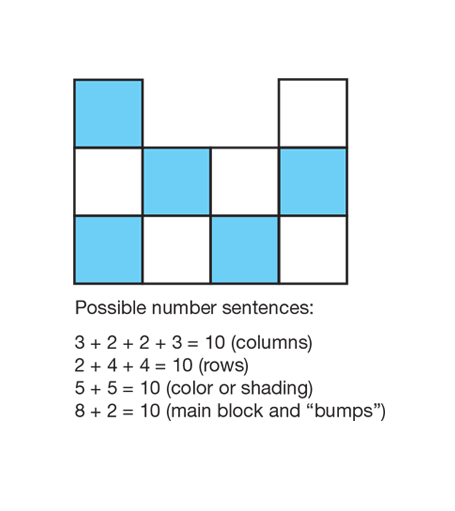
Create a new design. See Figure 2 for a sample design. Tell students to replicate this design with square-inch tiles and write a number sentence to describe it. Have different students write their number sentences on the board and show how each number sentence describes the design. Discuss the sentences with the class, emphasizing that there are usually different ways of representing the same problem.

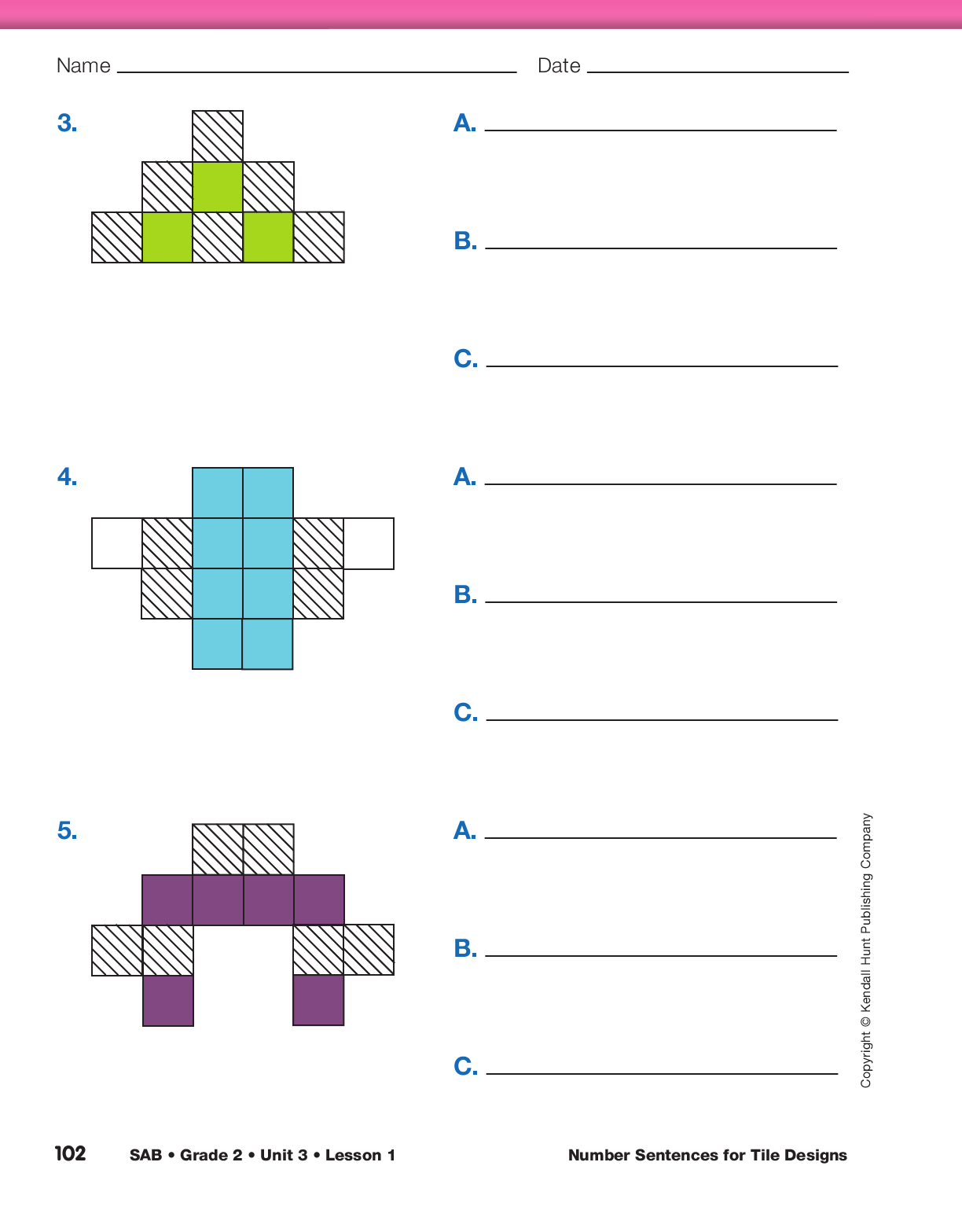
Ask students to open the Student Activity Book to the What’s My Number Sentence pages. Use the display of the What’s My Number Sentence pages in the Student Activity Book to explain to students that they will write number sentences for the designs. At this time, they answer only parts A and B for each design. They will complete part C later in the lesson.

As students are working, circulate asking:

Show me how the number sentences connect to the tile design.
Did your neighbor write a different number sentence?
Are you connecting the number sentence to the colors, columns, rows, or diagonals?

Encourage students to focus primarily on rows, columns, diagonals, or color shading at this point. This will make it easier for them to write number sentences that bear an observable relationship with the organization of the design.

Introduce True or False Number Sentences.
Display the following number sentences:

6 + 2 = 8
8 = 6 + 2
5 + 2 = 8
8 = 5 + 2

Discuss these number sentences using these or similar prompts:

Which statements are true? How do you know? Show me. (A and B)
Which statements are false? How do you know? Show me. (C and D)
How can Sentence A and Sentence B both be true? Show me how both are true. (6 cubes and 2 cubes make 8 cubes.)
If they are both true, how are they different? (The order is different, but they say the same thing.)

Write the following number sentences on a display one at a time.

8 = 8
8 = 10 − 2
6 + 2 = 2 + 6
6 + 2 = 4 + 4
6 + 2 = 8 + 0

For each number sentence, ask students to discuss the following with a partner:

Is the sentence true or false?
How can you show that the sentence is true (or false)? What tools can you use? (See Figure 3 for possible response for sentence D.)

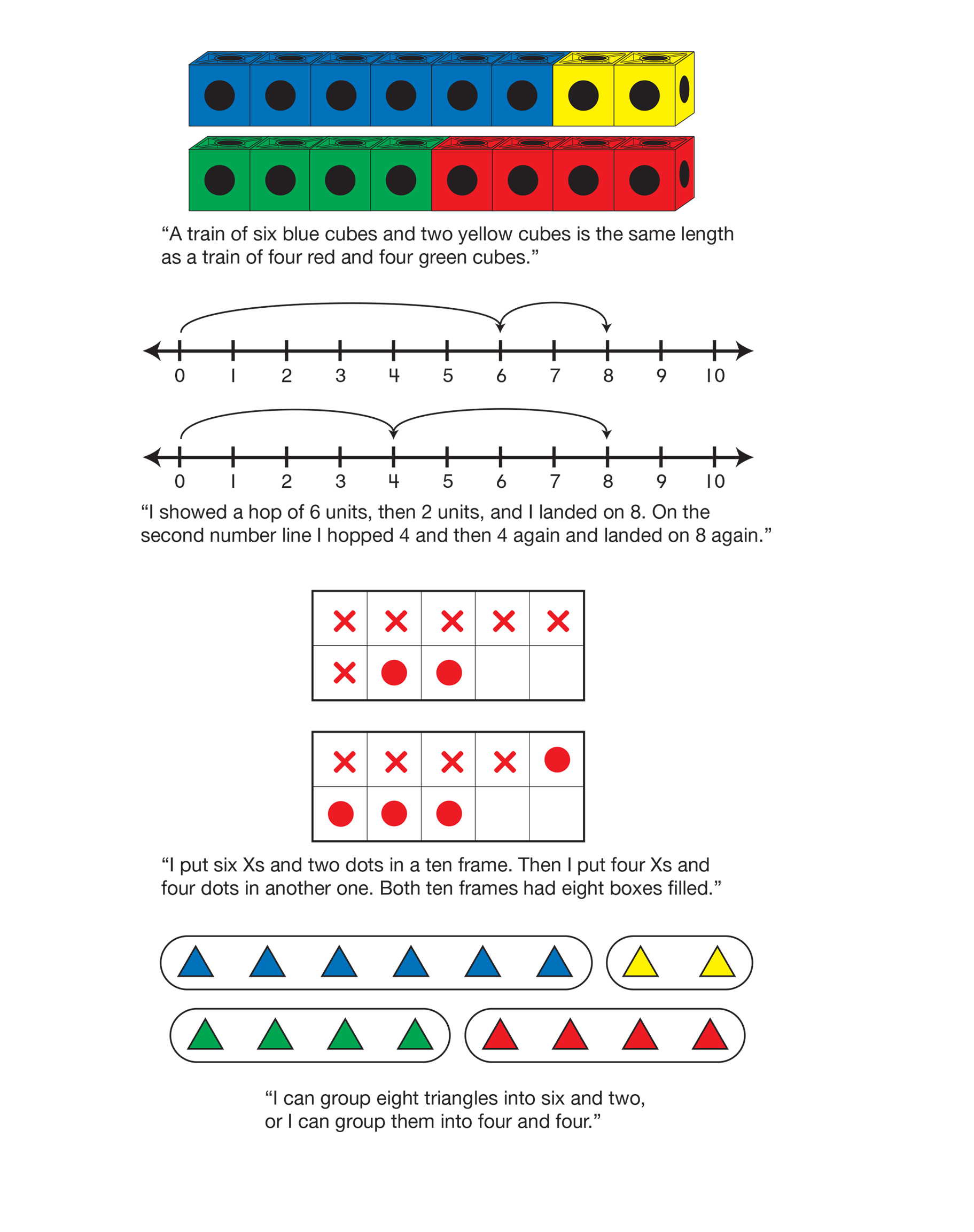
Encourage students to use the strategies and tools they have used in class for problem solving to prove whether the statements are true or not. For example, for Sentence D,
6 + 2 = 4 + 4, they can show a train of 6 blue and 2 yellow cubes and another train of 4 red and 4 green cubes, both trains totaling 8 cubes. Or they can describe counting on 2 from 6 and doubling 4, showing that both equal 8.

As students explain each number sentence, complete each conversation by representing the addition on both sides of the equal sign as follows:

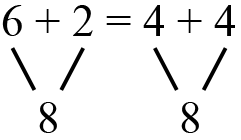
Ask students to share their methods by showing how they used the tools either verbally or in a picture.

Combine Number Sentences to Represent Equal Statements. Display again one of the tile designs from Figure 1. Have students recall the number sentences suggested to describe it and write the number sentences on a display, one above the other. Ask the students if they agree that all the number sentences are true and describe the tile design.

Rewrite two of the number sentences as one sentence with more than one addend on each side of the equal sign. For example, for the 3 x 3 square in Figure 1, you have number sentences of 3 + 3 + 3 = 9 and 5 + 4 = 9. Rewrite the sentences as one sentence: 3 + 3 + 3 = 5 + 4. See Figure 4.

Ask:

Can someone explain what I did to get 3 + 3 + 3? Where did this part come from? (the first number sentence)
What did we say 3 + 3 + 3 is equal to? (9)

Write a 9 immediately below as shown in Figure 4.

Where did 5 + 4 come from? (the second number sentence)
What did we say 5 + 4 is equal to? (9)
Can we say that 3 + 3 + 3 = 5 + 4 is a true statement? (Yes) Why or why not? (Both number sentences equal 9.)

Display another of your earlier tile designs and go through the same process and questions.

Represent Equal Statements for Tile Designs. Show the display of the first What’s My Number Sentence page and have students look at their own pages that they completed. Call on a volunteer to tell you the two number sentences he or she wrote for Question 1. Write the two number sentences on the display of Questions 1A and 1B. Two possible number sentences are 2 + 2 + 2 = 6 and 3 + 3 = 6.

Ask:

Do both these number sentences describe the same design? Show how each describes the design. (3 columns of 2 or 2 rows of 3 tiles)
Are the number sentences true? Show me that
2 + 2 + 2 = 6 is a true statement. Show me that
3 + 3 = 6 is a true statement. (Yes, both are true. I can show it with cubes.)

Write 3 + 3 = 2 + 2 + 2 on the line of Question 1C.

Ask:

Since 2 + 2 + 2 = 6 and 3 + 3 = 6, is 2 + 2 + 2 = 3 + 3 a true statement? (yes) Why or why not? (They both equal 6.) Show me.
What did I do to get this new number sentence? (You put an equal sign between two true number sentences.)

Have the student show, using tools or strategies, how 3 + 3 = 2 + 2 + 2. Represent the equality with the same notation as in Figure 4, showing both sides of the equal sign equal to 6.

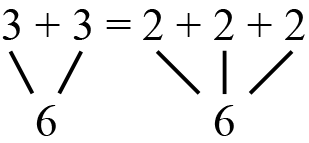
Ask the same questions about another student's number sentences for Question 2. In the same manner as for
Question 1C, write the appropriate number sentence that combines the two number sentences on line 2C. For example, write 3 + 3 + 3 = 4 + 3 + 2. Again, ask whether it is a true statement and have a student show or describe using strategies or tools. Use the same representation showing that both sides of the equation equal 9.

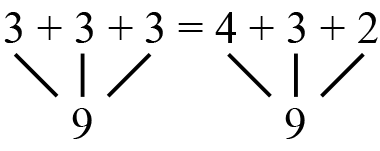
Have students work in pairs to complete Questions 3C, 4C, and 5C, combining the two number sentences into one with 2 or more addends on each side of the equal sign. Have them show or explain to each other how they know that the sentences are true.

ADVENTURE BOOK:

Student Activity Book: 101 102

Answers