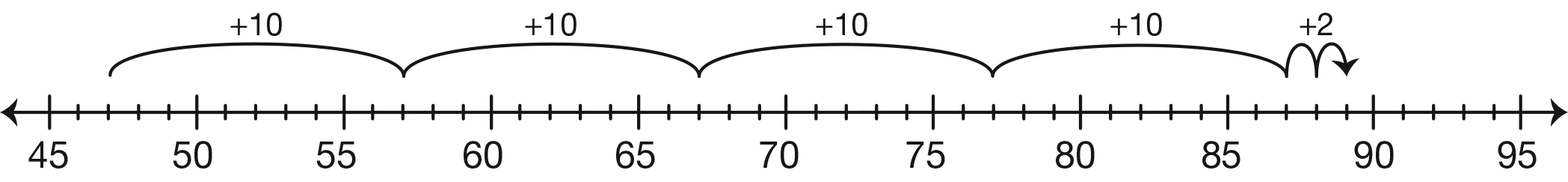Read Check It Out.
Begin this lesson by reading
the Adventure Book story “Check It Out.” This story
describes how Marcus solves problems using more
than one strategy to check his answers. The story
starts with Marcus and his classmates solving a
problem in different ways. Then their teacher gives
them a homework assignment to find an interesting
problem and solve it using many different strategies
to check their answers. Marcus then heads to the
grocery store to find and solve an interesting problem.
Pages 1–2
- What tools are the three children using to solve
the same problem? (connecting cubes, ten
frames, a 200 Chart, counters, and the
calculator)
- What other tools have we been using to solve
problems? (Possible response: number line)
- Who is correct? How did you solve the problem?
Have students share their strategies for solving the
problem. Encourage students to use the 200 Chart,
number line, coins, or connecting cubes to solve the
problem.
- Can someone show how they used the 200 Chart
to solve 15 + 18? (Possible strategy: Start at 18
and move one row below to add 10 and then
count on from 28 five more: 29, 30, 31, 32, 33 to
get an answer of 33.)
- Did anyone else use the 200 Chart but solve the
problem a different way? Can you show us?
(Possible response: Start at 15 and move one row
below to add 10 and then count on eight more to
get an answer of 33.)
- What are some ways you can check your answer?
(Solve the problem a different way and see if you
get the same answer. You can use a different tool
like a number line, coins, or counters.)
- How can you use your desk number line to solve
15 + 18? Show your neighbor. (Start at 15. To
skip count by 10, take one hop of 10 to 25, then 8
little hops to 33.)
- Did you both use the number line the same way?
Did you both get the same answer?
Ask students to share some number line strategies
with the class using the class number line. For example,
if a student knows the double of 15, start at 15
and then take another big hop of 15 to 30, then three
little hops to 33.
- Did you get the same answer using the 200 Chart
and the number line? (Answers will vary.)
Students should notice that they got the same
answer each time.
- How confident are you with your answer? Does it
seem reasonable? (Answers will vary.)
Since students solved the problem two ways and
got the same answer both times, they should be
confident with their answer.
Page 6
- What are some problems Mr. Montes may have
to solve as the owner of a grocery store?
(Possible responses: how much food to order;
how much to charge for the food; how much to
pay employees)
Page 8
- The price you pay for meat and vegetables
depends on how many pounds you buy. What
other items are weighed at the store? (Possible
response: fruit, candy, or nuts)
Page 10
- If Marcus’s pepper weighs exactly one pound, how
much will it cost? (98¢)
- Do you think Marcus’s pepper weighs more than
one pound or less? How did you decide?
Depending on students’ experiences with money and
grocery shopping, a few students may think 98¢ is a
lot of money for one pepper. You may want to pass
around a green pepper or an object that weighs one
pound. To give students a benchmark for weight in
pounds, discuss the weights of some common grocery
items. A gallon of milk, for instance, weighs
approximately eight pounds. A loaf of bread can
weigh one pound. See Materials Preparation.
Page 12
- Did the pepper weigh more or less than
one pound? (Since the pepper costs 47¢, it must
weigh less than one pound. In the picture, the
arrow on the scale is not pointing to one pound
so the pepper weighs less than one pound.)
Pages 13–14
- What did Marcus pull out of his pocket? Why
do you think he carries these items with him?
(Marcus finds connecting cubes. He carries these
tools to help him solve math problems.)
- Does Mr. Montes’ addition “check out”
all right? (Mr. Montes and Marcus agree. The
cost is 89¢.)
- Describe the strategies Marcus used to
check out Mr. Montes’ addition. (Marcus used connecting
cubes and he skip counted
by tens.)
- How might you have solved this problem?
What tools would you use?
Student pairs can solve the problem and share their
solution strategies. Encourage students to use a different
strategy to solve the problem.
Page 15
- When Marcus uses the 200 Chart, he starts on 40
and counts by tens to check the problem again.
Why does he start on 40? (The tomato sauce
costs
40¢.)
- Describe how Marcus might finish checking the
problem on the 200 Chart. (Start on 40; move 4
rows below saying 50, 60, 70, 80; count on 7,
then 2; 81, 82, 83, 84, 85, 86, 87, 88, 89.)
- Write a number sentence that shows how Marcus
used the 200 Chart to check the problem.
(40 + 10 + 10 + 10 + 10 + 7 + 2 = 89)
- How can you use a calculator to check Marcus’s
answer? ( 47 +
40 +
2 = 89¢)
- How can you use a number line to check Marcus’s answer? [See Figure 1.]
- Write a number sentence that shows how Marcus
used the number line to check the problem.
(47 + 10 + 10 + 10 + 10 + 2 = 89¢)
Page 16
- Why do you think Mr. Montes is glad that all
of his customers don’t check his math? (Possible
response: It takes time and other customers in
line might get impatient.)